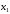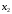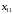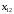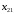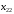математика. ДЗ для заочки по матемтике (экономисты). Решение. Составим и вычислим определители системы и ( j 1,2)
 Скачать 250.58 Kb. Скачать 250.58 Kb.
|
|
Примеры решения типовых задач Пример 1. Решить систему линейных уравнений 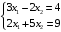 по правилу Крамера. по правилу Крамера. Решение. Составим и вычислим определители системы ∆ и 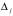 (j = 1,2): (j = 1,2):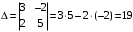 ; ; 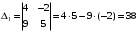 ; ;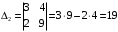 . . Определитель системы ∆ отличен от нуля, следовательно, система имеет единственное решение, которое вычисляется по формулам 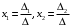 : :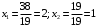 . .Ответ: 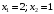 . .Пример 2. Решить систему линейных уравнений 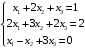 методом Гаусса. методом Гаусса.Решение. Составим расширенную матрицу системы и выполним соответствующие шаги прямого хода метода Гаусса. Имеем: 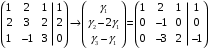 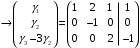 Символом 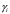 обозначена строка матрицы с номером i, преобразуемая на данном шаге. После стрелки указаны действия над строками матрицы, которые надо выполнить для получения соответствующей новой строки матрицы. обозначена строка матрицы с номером i, преобразуемая на данном шаге. После стрелки указаны действия над строками матрицы, которые надо выполнить для получения соответствующей новой строки матрицы.С помощью элементарных преобразований матрица приведена к треугольной. Полученная расширенная матрица соответствует системе уравнений 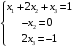 , которая эквивалентна исходной системе. , которая эквивалентна исходной системе. Решение этой системы находим обратным ходом метода. Из последнего уравнения 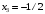 . Из второго уравнения . Из второго уравнения 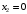 . Из первого уравнения . Из первого уравнения 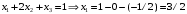 . .Ответ: 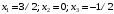 . .Пример 3. Показать, что векторы 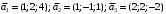 образуют базис в трехмерном пространстве, и разложить вектор образуют базис в трехмерном пространстве, и разложить вектор 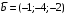 по этому базису. по этому базису.Решение. Составим матрицу, строками которой являются эти векторы, 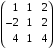 и вычислим ее определитель и вычислим ее определитель 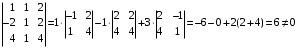 . . Следовательно, система векторов является линейно независимой и образует базис в трехмерном пространстве. Чтобы разложить вектор 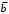 по этому базису, представим его в виде линейной комбинации базисных векторов по этому базису, представим его в виде линейной комбинации базисных векторов 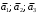 : : 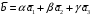 . Для нахождения чисел . Для нахождения чисел 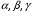 приравняем одноименные координаты вектора слева и вектора справа и получим систему уравнений приравняем одноименные координаты вектора слева и вектора справа и получим систему уравнений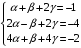 , , которую можно решить любым способом. Решим систему по правилу Крамера. Для этого составим и вычислим дополнительные определители системы 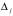 (j = 1,2,3): (j = 1,2,3):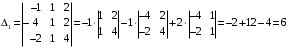 ; ;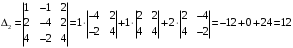 ; ;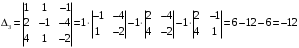 . .Тогда решение системы вычисляется по формулам 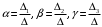 : :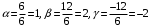 . . Ответ: 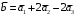 . .Пример 4. Найти максимум функции 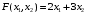 при ограничениях: при ограничениях: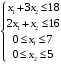 . . Решение. 1) Рисуем область допустимых значений. Первые два неравенства системы заменяем на равенства 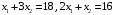 и рисуем соответствующие прямые по двум точкам. Прямые делят плоскость на две полуплоскости. Чтобы узнать, какая полуплоскость удовлетворяет нашим неравенствам, подставляем координаты точки О(0;0) в неравенства. Если ее координаты удовлетворяют неравенствам, то вся полуплоскость, где лежит эта точка, является решением неравенства. Если нет, то решением неравенства является другая полуплоскость. Третье и четвертое неравенства системы допустимых значений задают прямоугольник со сторонами 5 и 7. Получаем, что многоугольник OABCDEесть область допустимых значений. и рисуем соответствующие прямые по двум точкам. Прямые делят плоскость на две полуплоскости. Чтобы узнать, какая полуплоскость удовлетворяет нашим неравенствам, подставляем координаты точки О(0;0) в неравенства. Если ее координаты удовлетворяют неравенствам, то вся полуплоскость, где лежит эта точка, является решением неравенства. Если нет, то решением неравенства является другая полуплоскость. Третье и четвертое неравенства системы допустимых значений задают прямоугольник со сторонами 5 и 7. Получаем, что многоугольник OABCDEесть область допустимых значений.2) Рисуем прямую 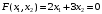 . Вектор ее нормали имеет координаты (2;3). Он задает направление возрастания целевой функции (мы ищем максимум функции). Последняя общая точка сдвинутого графика целевой функции и области допустимых решений OABCDE –это точка С. . Вектор ее нормали имеет координаты (2;3). Он задает направление возрастания целевой функции (мы ищем максимум функции). Последняя общая точка сдвинутого графика целевой функции и области допустимых решений OABCDE –это точка С. 3) Найдем ее координаты. Так как точка лежит на пересечении двух прямых 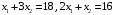 , то ее координаты удовлетворяют системе двух уравнений , то ее координаты удовлетворяют системе двух уравнений 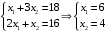 . Тогда . Тогда 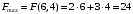 . .Ответ: 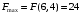 Пример 5. Предприятие имеет ресурсы A иB в количестве 240 и 120 единиц соответственно. Эти ресурсы используются при выпуске изделий двух видов, причем расход на изготовление одного изделия первого вида составляет 3 единицы ресурса А и 1 единицу ресурса B. Прибыль от реализации одного изделия первого вида составляет 20 ден.ед, а второго вида – 30 ден.ед. Составить экономико-математическую модель задачи. Решение. Пусть 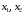 - количество изделий первого и второго вида, запланированных к производству. Тогда целевая функция – функция прибыли от реализации продукции – имеет вид - количество изделий первого и второго вида, запланированных к производству. Тогда целевая функция – функция прибыли от реализации продукции – имеет вид 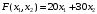 . . Составим множество допустимых значений. На изготовление изделий будет израсходовано ( 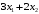 ) единиц ресурса А и ( ) единиц ресурса А и (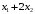 ) единиц ресурса B. Так как запасы ресурса А не превышают 240 единиц, то ) единиц ресурса B. Так как запасы ресурса А не превышают 240 единиц, то 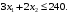 Ресурс B должен быть использован полностью, поэтому 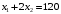 . Кроме того, изделий первого вида необходимо выпустить не менее, чем второго, поэтому . Кроме того, изделий первого вида необходимо выпустить не менее, чем второго, поэтому 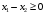 . . Итак, экономико-математическая модель задачи формулируется следующим образом: найти максимум линейной функции 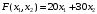 при ограничениях при ограничениях 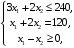 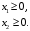 Пример 6. Имеется система из двух отраслей материального производства. За отчетный период исполнение баланса характеризуется данными таблицы. Найти вектор конечного продукта для нового вектора валового выпуска 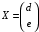 . Найти вектор валового выпуска для нового вектора конечного продукта . Найти вектор валового выпуска для нового вектора конечного продукта 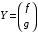 . .
Решение. 1) Найдем элементы матрицы прямых затрат A = ( 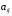 ) по формуле ) по формуле 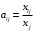 , используя данные таблицы: , используя данные таблицы: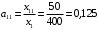 ; ; 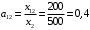 ; ;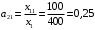 ; ; 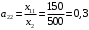 . .Матрица прямых затрат A= 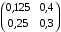 . .2) Проверим, что матрица продуктивная. Одним из критериев продуктивности матрицы является утверждение, что наибольшая из сумм элементов в столбцах матрицы А не превосходит единицы, причем есть хотя бы один столбец, где сумма меньше единицы. Проверим: 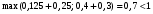 , , то есть матрица продуктивна. 3) Новый вектор валового продукта 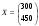 . Тогда соответствующий вектор конечного продукта на планируемый период равен: . Тогда соответствующий вектор конечного продукта на планируемый период равен: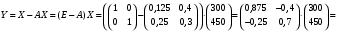 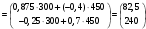 , здесь Е – единичная матрица. , здесь Е – единичная матрица. 4) Для нахождения вектора валового продукта по новому вектору конечного продукта 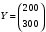 используем формулу используем формулу 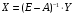 . . Для этого найдем обратную матрицу 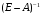 - матрицу полных затрат. - матрицу полных затрат.Так как матрица 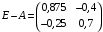 , ее определитель ее равен , ее определитель ее равен 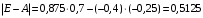 ; ; 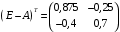 , , и присоединенная матрица имеет вид 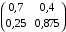 . . Тогда 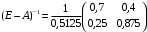 и вектор валового продукта равен: и вектор валового продукта равен: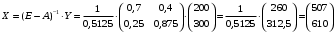 . .Задача 1. Решить систему линейных уравнений по правилу Крамера: 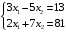 ; 2. ; 2. 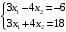 ; ;3. 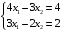 ; 4. ; 4. 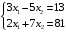 ; ;5. 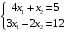 ; 6. ; 6. 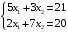 ; ;7. 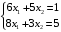 ; 8. ; 8. 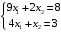 ; ;9. 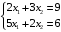 ; 10. ; 10. 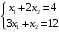 . .Задача 2. Решить систему линейных уравнений методом Гаусса: 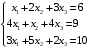 ; 2. ; 2. 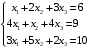 ; ; 3. 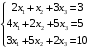 ; 4. ; 4. 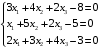 ; ; 5. 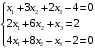 ; 6. ; 6. 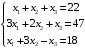 ; ; 7. 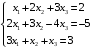 ; 8. ; 8. 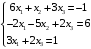 ; ; 9. 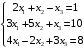 ; 10. ; 10. 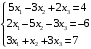 . .Задача 3. Показать, что векторы 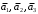 образуют базис в трехмерном пространстве, и разложить вектор образуют базис в трехмерном пространстве, и разложить вектор 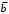 по этому базису. по этому базису.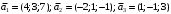 ; ; 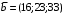 ; ; 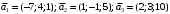 ; ; 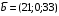 ; ; 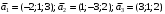 ; ; 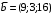 ; ; 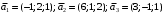 ; ; 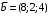 ; ; 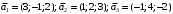 ; ; 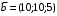 ; ;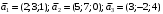 ; ; 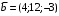 ; ;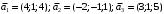 ; ; 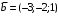 ; ;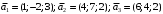 ; ; 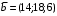 ; ;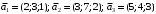 ; ; 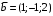 ; ;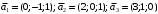 ; ; 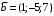 . .Задача 4. 1. Найти максимум функции 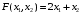 при ограничениях: при ограничениях: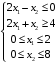 . .Найти максимум функции 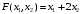 при ограничениях: при ограничениях: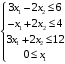 . .Найти максимум функции 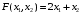 при ограничениях: при ограничениях: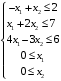 . .Найти максимум функции 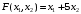 при ограничениях: при ограничениях: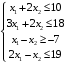 . .Найти максимум функции 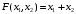 при ограничениях: при ограничениях: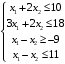 . .Найти минимум функции 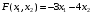 при ограничениях: при ограничениях: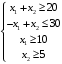 . .Найти минимум функции 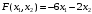 при ограничениях: при ограничениях: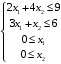 . .Найти минимум функции 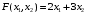 при ограничениях: при ограничениях: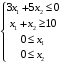 . .Найти минимум функции 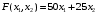 при ограничениях: при ограничениях: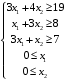 . .Найти минимум функции 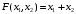 при ограничениях: при ограничениях: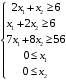 . .Задача 5. 1) Прядильная фабрика для производства двух видов пряжи использует три вида сырья - чистую шерсть, капрон и акрил. В таблице указано расход сырья в течение одного года и прибыль от реализации:
Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли:
2) На велосипедном заводе выпускают гоночные и дорожные велосипеды. Производство устроено так, что вместо двух дорожных велосипедов завод может выпустить один гоночный, причем гоночный велосипед приносит в 1,5 раза больше прибыли. Завод может произвести А дорожных велосипедов в день, однако склад может принять не более В велосипедов в день. Требуется составить ежедневный план выпуска велосипедов с целью максимизации суммарной прибыли:
Задача 6. Убедиться, что модель Леонтьева продуктивна. Найти вектор конечного продукта для нового вектора валового выпуска 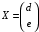 . Найти вектор валового выпуска для нового вектора конечного продукта . Найти вектор валового выпуска для нового вектора конечного продукта 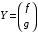 . .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||