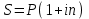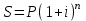4 задачи финмат доработка. Решение Составим уравнение эквивалентности Ответ
 Скачать 52.02 Kb. Скачать 52.02 Kb.
|
Задача 2Какой годовой антисипативной ставкой без капитализации можно заменить в контракте сложную учетную ставку 10 % (К=365), не изменяя финансовых последствий. Срок операции – 380 дней. Антисипативная ставка – это тоже учетная ставка. Дано: 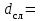 0,1 – годовая сложная учетная ставка; 0,1 – годовая сложная учетная ставка; 380/365 – срок финансовой операции в годах. 380/365 – срок финансовой операции в годах.Найти: 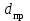 - эквивалентную простую учетную ставку. - эквивалентную простую учетную ставку.Решение: Составим уравнение эквивалентности 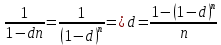 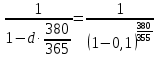 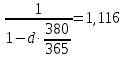 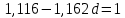 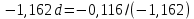 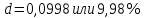 Ответ: годовая антисипативная ставка без капитализации равна 9,98% Задача 3Вексель номиналом 250 тыс. руб., выданный на 3 года 300 дней, учитывается по ставке 8 % годовых. Определить размер вексельного обязательства. Дано: 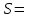 250 тыс. руб. – номинальная стоимость векселя, будущая сумма; 250 тыс. руб. – номинальная стоимость векселя, будущая сумма;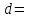 0,08 – годовая учетная ставка; 0,08 – годовая учетная ставка; 3 + 300/360 года – срок от момента учета векселя до даты погашения в годах; 3 + 300/360 года – срок от момента учета векселя до даты погашения в годах;Найти: 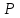 – сумму, полученную владельцем векселя, первоначальную сумму. – сумму, полученную владельцем векселя, первоначальную сумму.Решение: Чаще всего операции при банковском учете производятся по обыкновенным процентам (временная база k = 360 дней). При этом число дней между датой учета векселя и датой погашения берется точно. Если учетная ставка простая, то сумма, полученная держателем векселя: 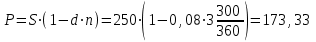 тыс. руб. тыс. руб.Если учетная ставка сложная, то сумма, полученная держателем векселя: 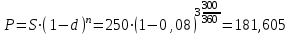 тыс. руб. тыс. руб.Размер вексельного обязательства определим по формуле: По простой процентной ставке 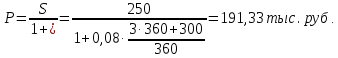 По сложной процентной ставке 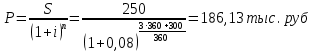 Ответ. Размер вексельного обязательства составит 173,33 тыс. руб., если применяется простая учетная ставка или 181,605 тыс. руб. – если сложная. По простой процентной ставке вексельное обязательство равно 191,33 тыс.руб., по сложной ставке – 186,13 тыс.руб. Задача 4 200 тыс.долларов США размещены на депозите. Курс на начало срока депозита составляет 73,98 руб. за 1 доллар, курс в конце операции 72,43 руб. Используя разные варианты расчета, сравнить сроки депозита при условии использования ставки по депозитам в рублях – 4,5% и в валюте – 1,5%. Дано: 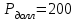 тыс. долл. США – первоначальная сумма вклада; тыс. долл. США – первоначальная сумма вклада;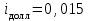 - ставка по депозитам в валюте; - ставка по депозитам в валюте;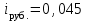 - ставка по депозитам в рублях; - ставка по депозитам в рублях;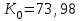 руб. за 1 доллар – курс на начало финансовой операции; руб. за 1 доллар – курс на начало финансовой операции;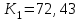 руб. за 1 доллар – курс в конце финансовой операции; руб. за 1 доллар – курс в конце финансовой операции;Найти: Сравнить сроки депозита. Решение: Срок депозита неизвестен. Но точно известен курс на конец финансовой операции. И он ниже, чем на начало финансовой операции. С каждого доллара потери из-за изменения валютного курса составят 1,55 руб. При этом и ставка по депозитам в валюте ниже, чем в рублях. Размещение на депозите средств в долларах не является целесообразным. Необходимо открывать депозит в рублях. В этом случае и ставка по депозитам выше и за счет изменения курса валюты будет прибыль. Чем больше срок депозита, тем больше прибыль. Так, при использовании сложной процентной ставки и сроке депозите в 5 лет наращенная сумма депозита в рублях составит: 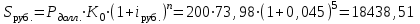 руб. руб.Наращенная сумма в долларах: 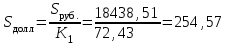 долл. долл.При использовании валютного вклада на тот же срок наращенные суммы составят: 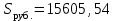 руб. и руб. и 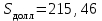 долл. долл.Таблица 1 Расчет наращенной суммы при депозите в рублях при различных сроках депозита
Таблица 2 Расчет наращенной суммы при депозите в долларах при различных сроках депозита
Задача 5За какой срок наращенная стоимость финансового инструмента номиналом 350 тыс. руб. не принесет убыток 50 тыс. руб. при условии, что начисляются проценты по ставке 11 % годовых раз в году и поквартально? Расчеты выполнить по процентной и учетной ставкам. Дано: 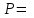 350 тыс. руб. – первоначальная сумма; 350 тыс. руб. – первоначальная сумма;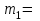 1 – число периодов начислений процентов в год; 1 – число периодов начислений процентов в год;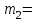 4 – число периодов начислений процентов в год; 4 – число периодов начислений процентов в год;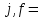 0,11 – сложная годовая номинальная процентная и учетная ставка; 0,11 – сложная годовая номинальная процентная и учетная ставка;Найти: 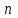 – срок финансовой операции в годах при котором финансовый инструмент не принесет убыток 50 тыс. руб. – срок финансовой операции в годах при котором финансовый инструмент не принесет убыток 50 тыс. руб.Решение: Происходит процесс наращения, начисляются проценты. При любом сроке наращения финансовый инструмент не будет приносить убытки. 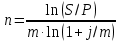 По условию сказано, что необходимо найти срок, при котором не будет убытка 50 тыс.руб., то есть наращенная сумму будет равна 300 тыс.руб. Такое возможно только при наличие инфляции или при учетной ставке, т.к. любое начисление процентов это наращение, т.е. прибыль, доход. 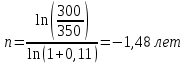 Решение задачи – некорректное, т.к. срок не может быть отрицательный. Находим срок наращения, если используется процентная ставка, проценты начисляются ежеквартально: 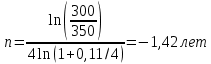 Находим срок наращения, если используется учетная ставка, дисконтирование процентов происходит раз в год: 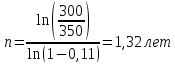 Находим срок наращения, если используется учетная ставка, дисконтирование процентов происходит ежеквартально: 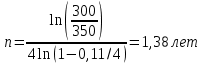 Ответ. При процентной ставке данная ситуация невозможно, т.к. в решение получается некорректный отрицательный срок. Финансовый инструмент принесет прибыль в 50 тыс. руб. через 1,32 лет если используется сложная учетная ставка с дисконтированием процентов раз в год. Финансовый инструмент принесет прибыль в 50 тыс. руб. через 1,38 лет если используется сложная учетная ставка с дисконтированием процентов ежеквартально. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||