3) Три завода
В магазинах №1 – 45% машин, №2 – 40% машин, №3 – 15% (в сумме 100%)
Из них стандартных машин из первого завода 70%, из второго – 80%, из третьего – 81%
Найти вероятность того что купленная машина - стандартная.
P(A)=0.45*0.7+0.4*0.8+0.15*0.81=0.7565=75%
4) 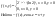
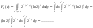 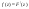 
|
3) Два стрелка стреляют в цель. Вероятность попадания первого – 0,8 , второго – 0,4. Нужно найти вероят., что первый поразил цель.
Цель поражена: 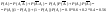
Цель поражена первым 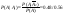
4) Двумерная случайная величина 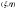 равномерно распределена в эллипсе равномерно распределена в эллипсе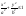 Определить Определить 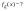
Решение: 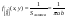 - совместная плотность распределения. - совместная плотность распределения.
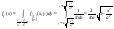
|
Локатор вращается.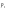 - вероятность обнаружения цели за один оборот без помех - вероятность обнаружения цели за один оборот без помех
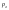 - есть помехи ,р – вероятность того что помехи создаются. Найти Р(Хотя бы один раз будет обнаружена цель за n оборот. с помехами) - есть помехи ,р – вероятность того что помехи создаются. Найти Р(Хотя бы один раз будет обнаружена цель за n оборот. с помехами)
Решение: следствие из ф-лыБернуллей: 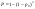
А – обнаруж. цели, Н1 – помехи создаются, Н2 – без помех.
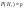 ; ;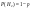 ; по ф-ле полной вероятности ; по ф-ле полной вероятности
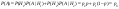 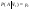 ; ; 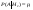
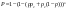 -ответ -ответ
4) 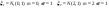
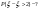
Решение:
Т К величины независимы и нормально распределены можно расписать по Лаполасу:
Пусть Z=x-y и из условия MZ=MX-MY=0-2=-2
DZ=DX+DY=1+1=2 Следовательно средне квадратичотклон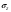 = =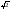
P(y2)=P(2) где a=2 и b=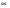 тогда по лаполасу тогда по лаполасу
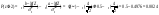
|
Лампы 0,1 0,2 0,3 0,4 – незав.  - приб. Определить вероятность, что - приб. Определить вероятность, что 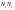 выйдут из строя выйдут из строя
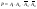 решение: решение:  4) 2 монеты кидают…… найти коэф корреляции 4) 2 монеты кидают…… найти коэф корреляции 
х-вероятн выпасть гербу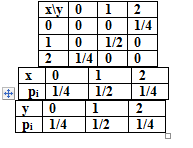
у-вероятн выпасть цифре
x=2-y отсюда  =-1 =-1
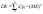

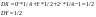
 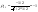
|
В цехе 20 станков, типа – 6 штук, типа B - 11, типа С – 3. Вероятность выпустить хорошую деталь для станка А – 0,5 , для станка В – 0,7 , С - 0,9. Каков процент хороших деталей выпускаемых цехом.
Решение: по формуле полной вероятности:
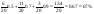
4) Случайная величина 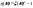 , закон распред. , закон распред. 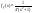 . Найти плотность распределения по . Найти плотность распределения по . .
Решение
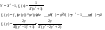
|
3) 0,6 – вероятность наблюдать облачность со спутника
0,95 - вероятность с которой данные передадут на Землю. Найти вероятность , что переданные данные об облачности верны.
Решается через формулу Байеса
  - облачность есть, - облачность есть,  - облачности нет - облачности нет
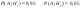
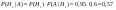
4) f(x,y) равномерно расперделена в Gf(x,y)=1/2
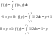 отсюда отсюда 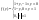
|
) По дороге едут груз и легковая машины, груз.в 4 раза больше чем легковая, вероятность того что груз. машина заед. на бензоколонку – 0,05 , а легковая – 0,15.
Найти с какой вероятностью машина покидающая бензозаправку – грузовая.
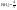 - легковая машина, - легковая машина, 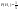 - грузовая. - грузовая.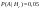 - вер-тьзапр. грузовой машины - вер-тьзапр. грузовой машины
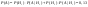 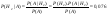
3) 2 машинистки одна напечатала 1/3 часть рукописей, вторая – 2/3.
Вероятность что первая ошиблась 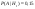 , вторая - , вторая - 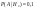
Найдена ошибка , какова вероятность, что ошиблась первая.
А – ошибка обнаружена
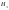 -печатала первая, -печатала первая, 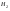 - печатала вторая - печатала вторая
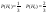
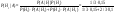 
|
4) 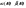 - 2 независ. случ. величины, равномерно распределены на отрезке [0,h], где - 2 независ. случ. величины, равномерно распределены на отрезке [0,h], где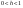 Найти вероятность, что корни уравнения Найти вероятность, что корни уравнения 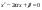 - комплексные. - комплексные.
Решение:
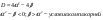 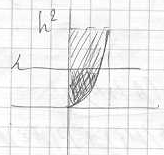
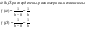
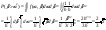
|
3) В первой урне 5 белых и 4 черных шара, во второй урне 4 белых и 2 черных шара.
Найти вероятность того, что вытащенный черный шар из первой урны.
Реш.:
Р(А) – вытащили черный шар; Р(Н1) – вытащили шар из первой урны;
Р(Н2) – вытащили шар из второй урны
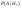 -если вытаскивают из 1-й урны, то шар черный -если вытаскивают из 1-й урны, то шар черный
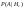 - если вытаскивают из 2-й урны, то шар черный - если вытаскивают из 2-й урны, то шар черный
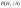 - если вытащили черный шар, то он из 1-й урны - если вытащили черный шар, то он из 1-й урны
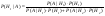 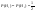 , ,  =4/9 =4/9 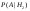 =2/6 =2/6
Ответ: 4/7
4) Найти 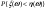 если если 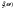 и и 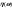 независимы, и независимы, и 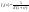 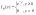
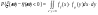 = =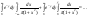
|
3) ВАЛ: равновозможны след.дефекты: 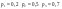 . Найти вероятность что деталь поступила в ремонт хотя бы с одной поломкой. . Найти вероятность что деталь поступила в ремонт хотя бы с одной поломкой.
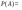 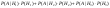 = =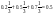
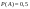 А-деталь поступила в ремонт хотя бы с одной поломкой А-деталь поступила в ремонт хотя бы с одной поломкой
4) 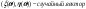 равномерно распред. в круге R=1, найти условную вероятность распред. равномерно распред. в круге R=1, найти условную вероятность распред.
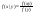 , , 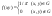 (1) (1)
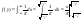 = =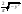
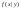 = =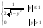 (2) Далее делим (1) на (2) получаем ответ. (2) Далее делим (1) на (2) получаем ответ.
|
3) Есть 18 стрелков, есть 4 группы.
В 1 группе 5 человек - попадает с вероятностью р=0,8
Во 2-ой - 7 чел, р=0,7; в 3-ей – 4 чел, р=0,6; в 4-ой - 2 чел, р=0,5
Какой группе принадлежит самый херовый или самый нормальный стрелок.
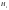 - стрелок из i-группы, i=1,2,3,4 - стрелок из i-группы, i=1,2,3,4
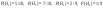 А – стрелок попал в цель. А – стрелок попал в цель.
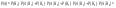
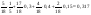
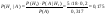 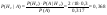
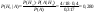 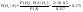
Ответ: - вероятно из второй группы.
|
В цехе 20 станков: 10 марки А, 6 марки В, 4 марки С. 0.8 0.7- вероятности изготовления отличных деталей. Найти какой процент отличных деталей выполняет цех
P(H1)=10/20=0.5; P(H2)=6/20=0.3 P(H3)=0.2
P(A)= P(H1)P(A|H1)+ P(H2)P(A|H2)+ P(H3)P(A|H3)=0.5*0.9+0.3*0.8+0.2*0.7=0.83=83%
4.дано 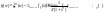
решение 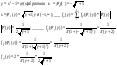
|
3)Радист сделал 3 вызова. Р того что первый дойдет=0.2 2-0.3 3-0.4 Какова вероятность того, что корреспондент вообще услышит вызов
Решение 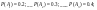 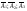 - ни один вызов не дойдет - ни один вызов не дойдет
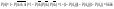
4) Найти плотность распределения случвеличины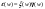 если величины независимы и распределены равномерно на интервале [-0.5|0.5] если величины независимы и распределены равномерно на интервале [-0.5|0.5]
Решение: Z=xy, F(z)=P(xyz)
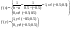 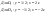 
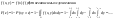 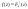 -искомая плотность -искомая плотность
|
3) Производительность первого станка в а раз меньше второго станка и в b раз меньше третьего станка.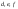 - вероятности получения брака. Вероятность брака -? - вероятности получения брака. Вероятность брака -?
А-взятая дет бракованая, Н1,Н2,Н3;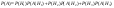
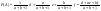 где где 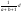 - вероятность того что деталь произв. первым станком. - вероятность того что деталь произв. первым станком.
3) Три стрелка стреляют в мишень по отдельности по 1 выстрелу и поражают мишень двумя пулями. Найти вероятность Р(А) – того что первый промажет
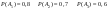
Решение: 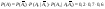
Т.к. 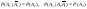
|
4) Случайная величина распределена на (a,b) по равномерному закону 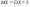
Найти 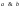
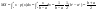
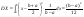 , т.к. , т.к. 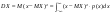
тогда получаем
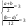 откуда получаема=0 , b=6 откуда получаема=0 , b=6
) 3 ящика с деталями 1-40 2-50 3-30
крашеных в первом 20, 2-10,3-15
Найти вероятность того, что случайно выбр. деталь - окрашенная
Решение:
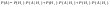
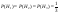
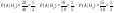
|
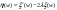 , ,  , , 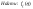
Решение:
Найдем 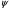 : : 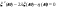 , , 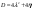 , , 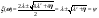
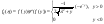
3) 3 Завода вероятность брака в деталях 1-0.2% 2-0.1% 3-нет
В партии 2000 деталей с 1-ого, 3000 со 2-ого, 5000 с 3 его
Найти вероятность того что случайная деталь из этой партии брак.
Решение: 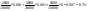
|
4) Дано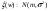 Найти плотность распределения случ величины Найти плотность распределения случ величины 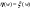
Решение
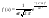 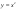 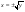 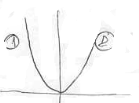
1 Область: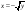 ; ;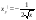
2 Oбласть: 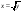 ; ; 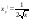
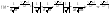 при y>0 и 0 при у<0 при y>0 и 0 при у<0
|
1-25 % брак 0.1%
2-40% брак 0.2%
3-35% брак 0.9%
с какой р на испытания попадет брак деталь с первого завода
Решение: Р=(0.25*0.001)/( 0.25*0.001+0.4*0.002+0.35*0.009)=считать сами!
Найти Р попадания в прямоугольник П 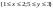 , если F(x,y) , если F(x,y)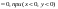 и и 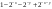 при при 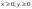
Решение
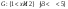
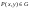 =F(b,d)-F(a,d)-F(b,c)+F(a,c) =F(b,d)-F(a,d)-F(b,c)+F(a,c)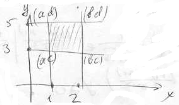
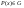 =1-2-2-2-5+2-7-1+2-1+2-3-2-4-(1-2-2-2-3-2-5)+ =1-2-2-2-5+2-7-1+2-1+2-3-2-4-(1-2-2-2-3-2-5)+
+(1-2-2-2-3+2-4)=2-7+2-3-2-4=1/128*(1+16-8)=9/128
|
3) Снаряд разрывается на осколки: на большие – с вероятностью 10%, на сред – 30%,
на малые – 60%. При попадании в броню большого снаряда пробив.ее с вероятностью 0,9
средний – 0,2 , малый – 0,05. Один осколок пробил броню. К какой группе он принадлежал с большей вероятностью?
Р(А)=0.1*0.9+0.3*0.2+0.6*0.05=0.18
А-пробил броню, H1-оторвавшийся большой,H2—средний;H3-маленький.
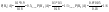
Наверняка ебанет первый, то есть БОЛЬШОЙ
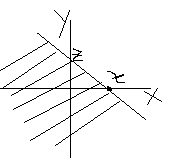
4) В декартовойсист. координат через точку (0,1) наугад проведена прямая. Найти закон распределения вероятностей расстояния от (0,0) до прямой.
φ
x
1
φ – равномерно распределена 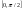
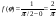 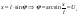
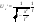 , , 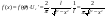
Т.о. 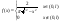
|
3) Два завода выпускают продукцию.вероятность того, что продукция с первого завода – 70%, того что со второго – 30%. Вероятность брака на первом 0, 1, вероятность брака на втором -0, 3 %. Найти вероятность, что наугад вытащенная продукция без брака.
А – деталь с браком.
Н1– деталь с первого завода
Н2 – деталь со второго завода
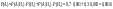
Без брака 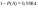
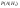 =0, 1 =0, 1 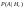 =0, 3 =0, 3
4) 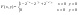 Найти Найти 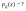
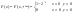
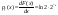
|
3)Первая галактика излучает с вероятностью 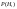 , вторая с вероятностью - , вторая с вероятностью - 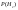 , ,
третья с вероятностью - 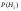 . Обнаружение первой галактики . Обнаружение первой галактики 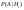 , второй – , второй – 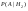 , третьей - , третьей - 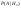 . Найти с какой вероятностью можно обнаружитьт излучение галактики, какой неизвестно. . Найти с какой вероятностью можно обнаружитьт излучение галактики, какой неизвестно.
Решение
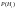 =0.23 ; =0.23 ;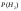 =0.31 ; =0.31 ; 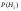 =0.46; =0.46; 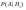 =0.002; =0.002; 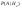 =0.0035; =0.0035; 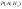 =0.0055 =0.0055
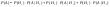 =4.07*10-3 =4.07*10-3
4) y=x2 Исследовать х и y на зависимость и некоррелятивность. y=x2 Исследовать х и y на зависимость и некоррелятивность.
Решение:
х и у зависимы так как y=x2
2) 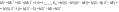
Потом по ф-ле
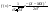 Следовательнонекоррелятивны Следовательнонекоррелятивны
|
Бросают 3 игр.кости, какова вероятность того, что при проведении 5-ти независимых испытаний выпадет ровно 2 раза по 3 единицы
Решение: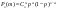 при одном испытании при одном испытании 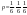 =1/216 тогда =1/216 тогда 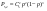 т. е. Р2(5)= = т. е. Р2(5)= =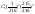 = =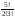 ………………. ……………….
4) 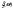 - распр. по норм. закону - распр. по норм. закону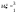 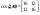 Найти Найти 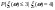
Решение Р(a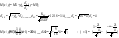
|
3) 96% продукции стандартно, с Р=0.98 схема контроля признает стандартную прод годной, с Р= 0.05 признает нестандартную годной. Опр. Р того что изделие стандартное
решение
А – изделие прошло контроль, Н1-прод стандарт 0.96 Н2-прод нестандарт 0.04
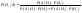 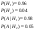
4) 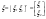 - -
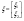 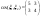 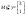 отсюда отсюда 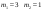
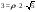 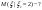
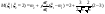
|
) В гараже 11 машин у 5 из них сломана коробка передач. 6 любых машин берут на ремонт. Найти вероятность Р что в ремонте нах-ся не меньше 2 машин со сломанной коробкой передач.
Решим задачу по ф-ле классической вероятности
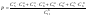 , где , где 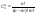 -количество сочетаний без повторений -количество сочетаний без повторений
4)Дан норм.распред. вектор 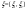 . Дан вектор ожидание . Дан вектор ожидание 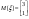
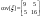 найти найти 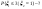
Решение: 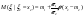
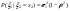 - -
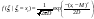 - а дальше считайте - а дальше считайте 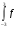 и получайте искомую Р и получайте искомую Р
|
3) Известно, что 0,0025 женщин и 0,05 мужчин дальтоники. Наугад выбирают человека. Он дальтоник, какова вероятность того что это мужчина?
Н1 – гипотеза, что выбран.чудик - бабища
Н2 – гипотеза, что выбран.чудик - мужик
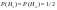 , А – событие, что люди дальтоники , А – событие, что люди дальтоники
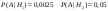 Надо найти, что Надо найти, что 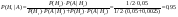
4)Дан 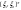 - нормально распределенный - нормально распределенный
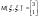 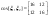 Найти Найти 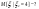
Решение:
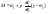 , , 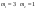 , , 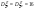 , (причем , (причем 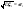 ) )
коэф. ковариации
|
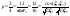 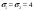
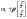 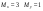 , , 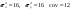
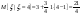
|
| |
 Скачать 498.79 Kb.
Скачать 498.79 Kb.