|
В треугольнике два угла равны48° и 79°. Найдите третий угол. Ответ дайте в градусах.
|
Решение:
Сумма углов треугольника равна 180°, поэтому третий угол равен:
180° – (48° + 79°) = 180° – 127° = 53°.
|
|
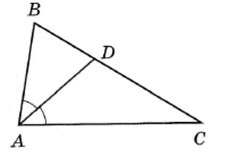
В треугольнике АВС известно, что 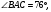
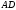 - биссектриса. Найдите угол ВАD. - биссектриса. Найдите угол ВАD.
Ответ дайте в градусах.
|
Решение:
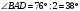 , так как биссектриса делит угол пополам. , так как биссектриса делит угол пополам.
Ответ: 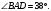
|
|
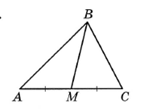
В треугольнике АВС известно, что АС = 54,
ВМ – медиана, ВМ = 45. Найдите АМ.
|
Решение: АМ = 54 : 2 = 27, так как медиана делит противоположную сторону пополам.
Ответ: АМ = 27.
|
|
 D D
В равнобедренном треугольнике АВС
с основанием АС внешний угол при
вершине С равен 132°. Найдите угол АВС.
Ответ дайте в градусах.
|
Решение:
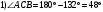 . .
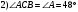 , так как углы при основании равнобедренного треугольника равны. , так как углы при основании равнобедренного треугольника равны.
 , сумма углов треугольника равна 180. , сумма углов треугольника равна 180.
Ответ: 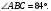
|
|

В остроугольном треугольнике АВС
проведена высота ВН, 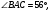
Найдите угол АВН.
Ответ дайте в градусах.
|
Решение:
Рассмотрим 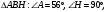
значит по теореме о сумме углов треугольника
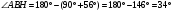
Ответ: 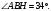
|
|
В треугольнике одна из сторон равна 29, а опущенная на нее высота равна - 12.
Найдите площадь треугольника.
|
Решение:
Площадь треугольника равна половине произведения основания на высоту, поэтому
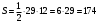
|
|

Точки М и N являются серединами сторон
АВ и ВС треугольника АВС, сторона
АВ равна 28, сторона ВС равна 44, сторона АС равна 42. Найдите МN.
|
Решение:
Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.
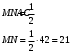
Ответ: 21.
|
|
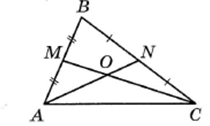
Точки М и N являются серединами сторон
АВ и ВС треугольника АВС соответственно.
Отрезки АN и СМ пересекаются в точке О,
АN = 18, СМ = 21. Найдите ОМ.
|
Решение:
Точки М и N являются серединами сторон
АВ и ВС, значит 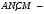 медианы, медианы,
поэтому поэтому точкой пересечения
делятся в отношении 2 : 1, считая от вершины
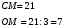
Ответ: 7.
|
|
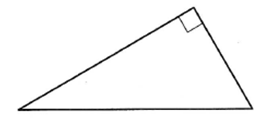
Катеты прямоугольного треугольника
равны 12 и 5. Найти гипотенузу этого треугольника.
|
Решение:
Квадрат гипотенузы равен сумме
квадратов катетов:

Ответ: 13.
|
|

В прямоугольном треугольнике катет и гипотенуза соответственно равны 7 и 25.
Найти второй катет этого треугольника.
|
Решение:
Квадрат гипотенузы равен сумме
квадратов катетов:

Ответ: 24.
|
|

В треугольнике АВС угол А равен 45°,
угол В равен 30°, ВС =  .Найдите АС. .Найдите АС.
|
Решение:
По теореме синусов:
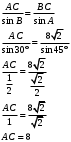
Ответ: 6.
|
|
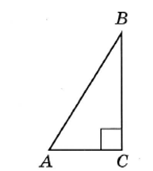
В треугольнике АВС угол С равен 90°,
АС = 14, АВ = 20. Найдите 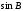 . .
|
Решение:
Синусом острого угла прямоугольного треугольника называется отношение
противолежащего катета к гипотенузе.
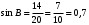
Ответ: 0,7.
|
|

В треугольнике АВС угол С равен 90°,
ВС = 12, АВ = 15. Найдите  . .
|
Решение:
Косинусом острого угла прямоугольного треугольника называется отношение
прилежащего катета к гипотенузе.
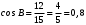
Ответ: 0,8.
|
|
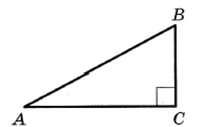
В треугольнике АВС угол С равен 90°,
АC = 8, ВС = 5. Найдите 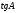 . .
|
Решение:
Тангенсом острого угла прямоугольного треугольника называется отношение
противолежащего катета к
прилежащему катету.
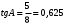
Ответ: 0,625.
|
|
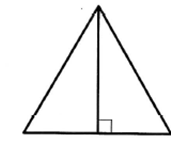
Сторона равностороннего треугольника
равна 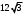 .Найдите его высоту. .Найдите его высоту.
|
Решение: Высота – медиана и биссектриса.
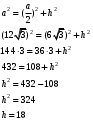
Ответ: 18.
|
|

На стороне треугольника АВС отмечена точка D так, что АD = 5, DС = 15. Площадь треугольника АВС равна 120.
Найдите площадь треугольника ВСD.
|
Решение:
Площади треугольников, имеющих одинаковые высоты относятся как основания.
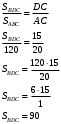
Ответ: 90.
|
|
В треугольнике АВС АВ = 15, ВС = 8,
 . .
Найдите площадь треугольника АВС.
|
Решение:
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
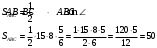
Ответ: 50.
|
|
Синус острого угла А треугольника АВС
равен 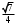 . Найдите косинус угла А. . Найдите косинус угла А.
|
Решение:
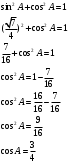
Ответ: 0,75
|
|
   
М
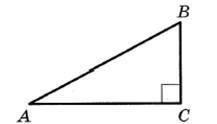
В треугольнике АВС угол С равен 90°
М – середина АВ, АВ = 42, ВС = 30.
Найдите СМ.
|
Решение:
В прямоугольном треугольнике середина гипотенузы является центром описанной окружности , значит
СМ = АМ = ВМ = 42 : 2 = 21
Ответ: 21
|
|

Биссектриса равностороннего треугольника
равна 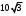 . Найдите его сторону. . Найдите его сторону.
|
Решение:
Любая биссектриса равностороннего треугольника является его медианой и высотой.
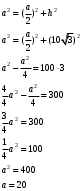
Ответ: 20.
|
 Скачать 248.16 Kb.
Скачать 248.16 Kb.