Документ Microsoft Word. Решение. Так как 1 2 5 3, то 2 n 5 2 3 58 Данный код однозначно декодируемый

• Название: Решение. Так как 1 2 5 3, то 2 n 5 2 3 58 Данный код однозначно декодируемый
• Дата: 11.01.2022
• Размер: 90.93 Kb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Решение; #328049

Контрольное задание No 1
1. Вычислить количество информации выдаваемой источником, если размерность алфавита 𝑋 = {𝑥1, 𝑥2, ... , 𝑥6} равна 𝑚 = 6.

Вероятность появления события
𝑝1 = 0,05; 𝑝2 = 0,15; 𝑝3 = 0,05; 𝑝4 = 0,4; 𝑝5 = 0,2; 𝑝6 = 0,15

3. Используются следующие кодовые слова длиной 𝑛 = 3 равномерного кода
𝐴 → (000);
𝐾 → (010);
𝑁 → (001);
𝐷 → (111).
𝐸 → (100).
Удовлетворяет ли код неравенству Крафта?

Решение. Так как 𝑛₁ = 𝑛₂ = ⋯ = 𝑛₅ = 𝑛 = 3, то 𝑚2^-n = 5 ∙ 2⁻³ = 5/8 < 1.


Данный код однозначно декодируемый,

4. Пусть используется префиксный код со словами:
𝐴 → (00);
𝐾 → (10);
𝑁 → (010);
𝐷 → (110);
𝐸 → (111).
Вероятности символов источника характеризуются множеством {𝑃(𝐴), ... , 𝑃(𝐸)} → {𝑝1 =1/2 , 𝑝2 = 1/4 , 𝑝3 = 1/8 , 𝑝4 = 1/16 , 𝑝5 = 1/16}. Вычислить среднюю длину кодового слова.

L_n=1/2*2+1/4*2+1/8*3+1/16*3+1/16*3=1+0,5+ 0,375 = 9/4=2.25

5. Источник формирует символы 𝑋 = {𝑥1, 𝑥2} c вероятностями {𝑝1 = 9/10 , 𝑝2 = 1/10}. Имеется блоковый источник с трехкратным расширением 𝑋3 = {𝑐1, 𝑐2, 𝑐3, 𝑐4, 𝑐5, 𝑐6, 𝑐7, 𝑐8}. Для кодирования блокового источника применяется префиксный код:

𝑐1 → (1);

𝑐2 → (011);

𝑐3 → (010);

𝑐4 → (001);

𝑐5 → (00011);

𝑐6 → (00010);

𝑐7 → (00001);

𝑐8 → (00000).

p1*p1*p1 = 9/10 * 9/10 * 9/10 = 0.729

p1*p1*p2 = 9/10 * 9/10 * 1/10 = 0.081

p1*p2*p1 = 9/10 * 9/10 * 1/10 = 0.081

p1*p2*p2 = 9/10 * 1/10 * 1/10 = 0.009

p2*p1*p1 = 1/10 * 9/10 * 9/10 = 0.081

p2*p2*p1 = 1/10 * 1/10 * 9/10 = 0.009

p2*p1*p2 = 1/10 * 9/10 * 1/10 = 0.009

p2*p2*p2 = 1/10 * 1/10 * 1/10 = 0.001
5.1. Вычислить энтропию источника.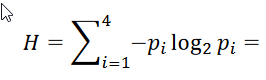



𝐻 = -(9/10*log₂9/10+1/10*log₂1/10)= - (−0.152 −3.322)= 3,474 бит/символ

5.2. Вычислить энтропию блокового источника.

H=

= 1.40

5.3. Вычислить среднюю длину слова декодируемого кода.

L_n=0.729*1+0.081*3+0.081*3+0.009*3+0.081*5+0.009*5+0.009*5+0.001*5=1.742

5.4. Вычислить среднюю длину слова на один символ источника 𝑋.

L_n/n=1.742/3=0.58

6. Показать, что группа 𝐺 = < {0,1, 2, 3, 4, 5}; +; 0> содержит подгруппы порядков: 1, 2, 3 и 6.

G

+	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	2	3	4	5	0
2	2	3	4	5	0	1
3	3	4	5	0	1	2
4	4	5	0	1	2	3
5	5	0	1	2	3	4

+	0	4	5
0	4	5	0
4	5	0	4
5	0	4	5

7. Найти расстояния Хэмминга векторов:

𝑑𝑖𝑠𝑡(1, 0, 0, 1, 1, 1, 0; 1, 1, 1, 0, 1, 0, 0) = 4,

1	0	0	1	1	1	0
1	1	1	0	1	0	0

𝑑𝑖𝑠𝑡(1, 2, 2, 1, 1, 1; 2, 1, 1, 0, 1, 0) =5

1	2	2	1	1	1
2	1	1	0	1	0

8. Построить порождающую 𝐺 и проверочную 𝐻 матрицу линейного группового кода с проверкой на четность с параметрами [𝑛; 𝑛 ‒1; 2], 𝑘 = 3

k - количество столбцов

9. Показать построение и реализацию принципиальной схемы кодера, используя проверочную𝐻 матрицу (п. 8)