ПЗ4 Маслобойникова ЭБ(с)-92 7 вариант. Решение Так как суммарная мощность поставщиков равна суммарному спросу потребителей, то есть
 Скачать 315.79 Kb. Скачать 315.79 Kb.
|
|
ПЗ № 4 ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА ПОСТАВОК 7 вариант Маслобойникова Вика, ЭБ(с)-92 Условие: Имеются четыре завода по производству железобетонных конструкций 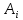 (i=1,4), с годовым выпуском ЖБК - (i=1,4), с годовым выпуском ЖБК - 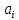 (i= (i=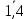 ) тыс. шт. Известны пять строительных площадок ) тыс. шт. Известны пять строительных площадок 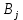 (j=1,5) и их потребности в ЖБК (j=1,5) и их потребности в ЖБК 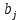 (j=1,5) тыс. шт. (j=1,5) тыс. шт. Затраты на поставку 1 конструкции от i-го завода к j-му пункту строительства составляют величину 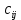 (i=1,4), (j=1,5) тыс. руб./шт. (i=1,4), (j=1,5) тыс. руб./шт. В задаче требуется составить такой план поставок железобетонных конструкций, который обеспечил бы минимальные суммарные затраты на поставку. 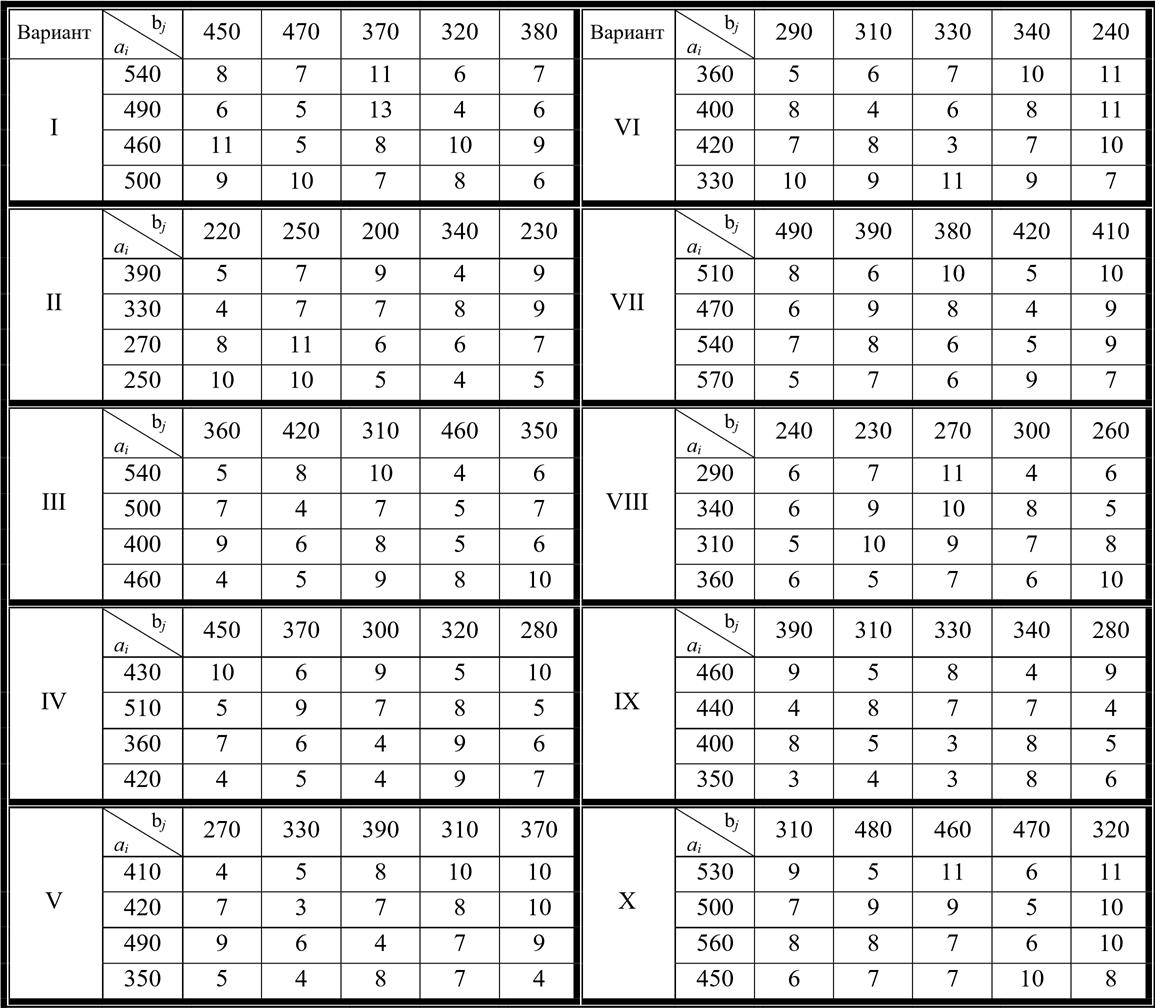 Решение: 1. Так как суммарная мощность поставщиков равна суммарному спросу потребителей, то есть: 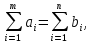 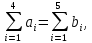 где i – номер поставщика; m – количество поставщиков; j – номер потребителя; n – количество потребителей; ai – мощность i-го поставщика; bj – спрос j-го потребителя; 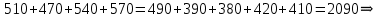 будем иметь дело с математической моделью закрытой транспортной задачи. Математическая модель закрытой транспортной задачи (целевая функция + система ограничительных условий): 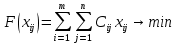 , ,где Cij – затраты на перевозку единицы продукции от i-го поставщика j-му потребителю; хij – объем продукции, перевозимой от i-го поставщика j -му потребителю; 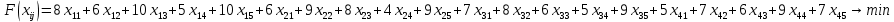 Суммарные затраты на перевозку продукции от всех поставщиков всем потребителям должны быть минимальными. Суммарный объем продукции, перевозимой от i-го поставщика всем j-м потребителям, должен быть равен мощности этого поставщика: 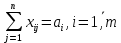 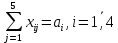 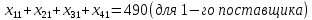 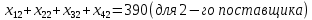 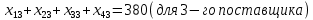 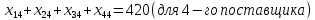 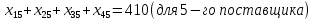 Построим первый опорный план транспортной задачи, используя метод северо-западного угла.
Первой заполнялась клетка А1В1, которая расположена в левом верхнем углу. Так как A1 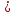 B1, то первый завод (поставщик) реализует свою продукцию первому потребителю (строительная площадка), удовлетворив все его потребности B1, то первый завод (поставщик) реализует свою продукцию первому потребителю (строительная площадка), удовлетворив все его потребности  в остальных ячейках столбца ставим прочерки. При этом, в запасе у него останется 20 тыс. шт. (А1В2). Далее рассматривается клетка А2В2. У второго потребителя потребность в ЖБК составляет 390, при этом первый завод уже не может предоставить свою продукцию в полном объеме, а только 20 тыс. шт в остальных ячейках столбца ставим прочерки. При этом, в запасе у него останется 20 тыс. шт. (А1В2). Далее рассматривается клетка А2В2. У второго потребителя потребность в ЖБК составляет 390, при этом первый завод уже не может предоставить свою продукцию в полном объеме, а только 20 тыс. шт  обратимся ко второму заводу, который может предоставить 370 тыс. шт., тем самым, покрыв потребность второго потребителя в ЖБК. В оставшихся ячейках также ставим пропуски. Третий потребитель может частично удовлетворить свою потребность, приобретя ЖБК у второго завода, так как остаток равен 100 (470-370), а далее у третьего завода, приобретя 280 тыс. шт. Так как потребность удовлетворена, ставим пропуски в оставшихся. Четвертый потребитель не может приобрести ЖБК у первого и второго завода, так как выпуск исчерпан, при этом, у третьего завода осталось 260, значит, возьмем остаток у него, и дополним недостачу у 4 завода, тем самым реализуем потребность четвертой строительной площадки в полном объеме. Пятый потребитель приобретет ЖБК у пятого завода, его потребность будет полностью удовлетворена (A4=B5). обратимся ко второму заводу, который может предоставить 370 тыс. шт., тем самым, покрыв потребность второго потребителя в ЖБК. В оставшихся ячейках также ставим пропуски. Третий потребитель может частично удовлетворить свою потребность, приобретя ЖБК у второго завода, так как остаток равен 100 (470-370), а далее у третьего завода, приобретя 280 тыс. шт. Так как потребность удовлетворена, ставим пропуски в оставшихся. Четвертый потребитель не может приобрести ЖБК у первого и второго завода, так как выпуск исчерпан, при этом, у третьего завода осталось 260, значит, возьмем остаток у него, и дополним недостачу у 4 завода, тем самым реализуем потребность четвертой строительной площадки в полном объеме. Пятый потребитель приобретет ЖБК у пятого завода, его потребность будет полностью удовлетворена (A4=B5).В результате получен первый опорный план, который является допустимым, так как все потребность строительных площадок удовлетворена, а план соответствует системе ограничений транспортной задачи. Таким образом, транспортные затраты составят: F = 8*490 + 6*20 + 9*370 + 8*100 + 6*280 + 5*260 + 9*160 + 7*410 = 15460. Теперь построим первый опорный план транспортной задачи, используя способ минимального элемента матрицы затрат.
В матрице стоимостей С=[сij] отыскивается клетка, содержащая наименьший элемент сij, в эту клетку записывается поставка xij = min (ai,bj). В данном случае, min сij = 4 находится в клетке A2B4  заносим поставку в клетку А2В4: x24 = 420. Так как спрос потребителя B4 удовлетворен, то столбец B4 исключается из дальнейшего распределения (вычеркивается). заносим поставку в клетку А2В4: x24 = 420. Так как спрос потребителя B4 удовлетворен, то столбец B4 исключается из дальнейшего распределения (вычеркивается). Далее вновь отыскиваем минимальное значение сij из оставшихся после вычеркивания клеток  min сij = 5 находится в клетке A4B1 ⇒ заносим поставку в клетку А4В1: x41 = 490. Так как спрос потребителя B1 удовлетворен, то столбец B1 исключается из дальнейшего распределения (вычеркивается). min сij = 5 находится в клетке A4B1 ⇒ заносим поставку в клетку А4В1: x41 = 490. Так как спрос потребителя B1 удовлетворен, то столбец B1 исключается из дальнейшего распределения (вычеркивается). Следующее минимальное значение сij из оставшихся после вычеркивания клеток ⇒ min сij = 6 находится в клетках A1B2, A3B3, A4B3. Выберем клетку А1В2 ⇒ заносим поставку в клетку А1В2: x12 = 390. Так как спрос потребителя B2 удовлетворен, то столбец B2 исключается из дальнейшего распределения (вычеркивается). Следующее минимальное значение сij из оставшихся после вычеркивания клеток ⇒ min сij = 6 находится в клетках A3B3, A4B3. Выберем клетку А3В3 ⇒ заносим поставку в клетку А3В3: x33 = 380. Так как спрос потребителя B3 удовлетворен, то столбец B3 исключается из дальнейшего распределения (вычеркивается). Из оставшихся клеток, минимальное значение сij имеет клетка А4В5, которая равна 7 ⇒ (те же действия производим с последим столбцом). Таким образом, транспортные затраты составят: F = 5*490+6*390+6*380+4*420+10*120+9*50+9*160+7*80=12400. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
