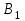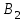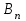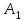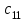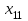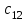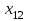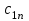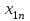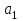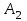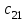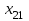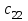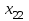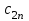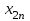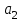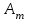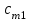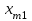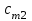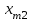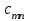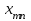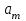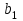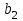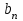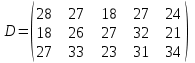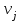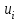Лекция 4.. Решение транспортной задачи методом потенциалов Симплексный метод для решения задач линейного программирова
 Скачать 140.79 Kb. Скачать 140.79 Kb.
|
|
«Нахождение начального решения транспортной задачи. Решение транспортной задачи методом потенциалов» Симплексный метод для решения задач линейного программирования является универсальным, он позволяет решить любую задачу, но решение иных задач связано с трудоемкими расчетами. Можно выделить класс задач, которые решаются более простыми специальными методами. К числу таких задач относятся так называемые транспортные задачи. Классическая транспортная задача - о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов отправления в пункты назначения. Классическая транспортная задача (сокращенно ТЗ) формулируется следующим образом. В пунктах отправления 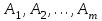 , которые будем называть также поставщиками, сосредоточены запасы однородного груза в количествах , которые будем называть также поставщиками, сосредоточены запасы однородного груза в количествах 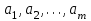 соответственно. В пункты назначения соответственно. В пункты назначения 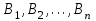 , именуемые потребителями, надлежит доставить соответственно , именуемые потребителями, надлежит доставить соответственно 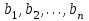 единиц груза. единиц груза.Известен транспортный тариф 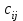 - стоимость перевозки единицы груза из пункта - стоимость перевозки единицы груза из пункта 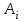 в пункт в пункт 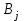 , , 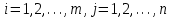 . Требуется составить такой план перевозок груза, при котором общая стоимость F всех перевозок была бы наименьшей, при этом все заявки были бы выполнены. . Требуется составить такой план перевозок груза, при котором общая стоимость F всех перевозок была бы наименьшей, при этом все заявки были бы выполнены. В термин "транспортный тариф" вкладывается условное понимание стоимости единицы груза - это может быть себестоимость, расстояние, тариф, время, расход топлива или электроэнергии и др. Пусть суммарные запасы грузов у поставщиков равны суммарным потребностям потребителей: 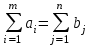 Это условие называется условием баланса. Если для ТЗ условие баланса выполняется, то модель ТЗ называется закрытой, если условие баланса не выполнено, то модель ТЗ - открытая. Составим математическую модель ТЗ. Пусть 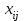 - количество груза, которое поставщик - количество груза, которое поставщик 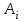 отправляет потребителю отправляет потребителю 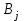 ( (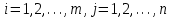 ) со стоимостью перевозок ) со стоимостью перевозок 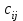 . Данные задачи можно представить в виде таблицы 1. . Данные задачи можно представить в виде таблицы 1.Таблица 1.
По смыслу своему величины 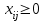 и должны удовлетворять следующим ограничениям: и должны удовлетворять следующим ограничениям:Из пункта 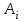 все запасы должны быть вывезены (ограничения по ресурсам): все запасы должны быть вывезены (ограничения по ресурсам): 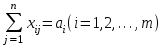 ; ;Заявки потребителей 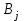 должны быть выполнены (ограничения по потребностям): должны быть выполнены (ограничения по потребностям): 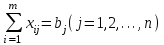 . .Затраты на перевозку 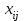 единиц груза из пункта поставки единиц груза из пункта поставки 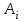 в пункт потребления в пункт потребления 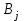 составляют составляют 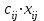 рублей; общая же стоимость всех перевозок рублей; общая же стоимость всех перевозок 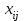 равна сумме всех таких затрат: равна сумме всех таких затрат: 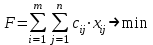 Математическая постановка ТЗ состоит в следующем: составить план перевозок 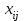 , удовлетворяющих системе ограничении: , удовлетворяющих системе ограничении: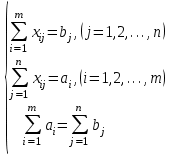 , ,условию неотрицательности: 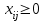 , , 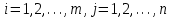 , при котором целевая функция достигает своего минимума: , при котором целевая функция достигает своего минимума: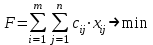 Из математической модели видно, что ТЗ является частным случаем общей задачи линейного программирования. В общей теории линейного программирования доказаны следующие теоремы: Теорема 1. Транспортная задача при выполнении условия баланса всегда имеет решение. Теорема 2. Система ограничений транспортной задачи содержит т+п-1 линейно-независимых уравнений. При решении задач практический смысл теоремы 2 заключается в следующем: число назначенных перевозок равно т+п-1. Процедура решения ТЗ будет состоять в последовательном улучшении опорных планов и проверки их на оптимальность. Методы построения начального плана. Существует несколько методов построения первоначального опорного плана ТЗ (опорный план - план, удовлетворяющий системе ограничений и условию неотрицательности). Рассмотрим только два из них: метод северо-западного угла и метод наименьшей стоимости. Как уже отмечалось, в опорном плане не более r = m + n - 1 переменных 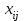 ,отличных от нуля. Если таких переменных равно r, то такой план называют невырожденным, в противном случае - вырожденным. ,отличных от нуля. Если таких переменных равно r, то такой план называют невырожденным, в противном случае - вырожденным. Метод северо-западного угла.Назначение перевозок начинаем с левой верхней клетки (северо-западный угол). Сравнивая ресурсы поставщика и потребности потребителя, назначаем максимально возможную перевозку. Если ресурсов поставщика недостаточно, то переходим к следующему поставщику. Если ресурсов у поставщика достаточно, то назначив нужную перевозку первому потребителю, переходим к следующему потребителю. При назначении перевозок для удобства записываем остаток ресурсов (потребностей); если ресурсы закончились или потребности удовлетворены, то ставим букву "к" (конец). Если при назначении перевозки одновременно закончились запасы ресурсов у поставщика и удовлетворены потребности потребителя, то из "игры" выводим только одного участника, другому оставляем нуль запасов или нуль потребностей. Метод наименьшей стоимости. Выбираем клетку с наименьшей тарифной ставкой и назначаем максимально возможную перевозку. Если запасы закончились или потребности удовлетворены, то поставщика или потребителя исключаем. Среди оставшихся клеток снова выбираем клетку с наименьшей стоимостью и назначаем максимально возможную перевозку. Если в результате назначения перевозки закончились запасы поставщика или удовлетворены потребности потребителя, то его исключаем из дальнейшего рассмотрения. Метод потенциалов построения оптимального плана. Наиболее простым методом решения ТЗ является метод потенциалов. Потенциалами называются условные числа 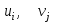 приписанные определенным образом каждому поставщику и потребителю. приписанные определенным образом каждому поставщику и потребителю. Теорема 3( условие оптимальности плана). Сумма потенциалов поставщика и потребителя равна тарифной ставке для занятых клеток; сумма потенциалов поставщика и потребителя не превышает тарифную ставку для свободных клеток: 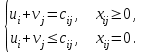 Замечание. Опорный план должен быть невырожденным. Алгоритм решения транспортной задачи: Строим начальные планы методом северо-западного угла и наименьшей стоимости, из них выбираем лучший. Находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана: 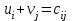 Проверяем второе условие оптимальности плана для свободных клеток 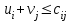 . Если оно выполнено, то план оптимален. Если не выполнено, то улучшаем план. . Если оно выполнено, то план оптимален. Если не выполнено, то улучшаем план.4. Улучшение плана. a) при невыполнении второго условия оптимальности плана в клетку заносим нарушение 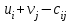 сo знаком "+". Такие клетки называются потенциальными; сo знаком "+". Такие клетки называются потенциальными; среди всех потенциальных клеток выбираем клетку с наибольшим нарушением; строим для выбранной клетки замкнутый контур, состоящий из вертикальных и горизонтальных отрезков прямой, причем вершины контура лежат в занятых клетках, за исключением той клетки, для которой строится контур. Виды контуров приведены на рисунке 1;  вершины контура поочередно помечаем, знаками "+","-", начиная с клетки, для которой построен контур; е) среди клеток, помеченных знаком "-", выбираем наименьшую перевозку. На эту величину увеличиваем перевозки в клетках, помеченных знаком "+", и уменьшаем вклетках, помеченных знаком "-". В результате переназначения перевозок освобождается одна клётка. 5.Вновь полученный план проверяем на оптимальность. Порядок выполнения заданий Задание. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
Решение. 1. Построим начальный план двумя методами: методом северо-западного угла и методом наименьшей стоимости, и выберем тот план, который будет наилучшим, то есть получим минимальные затраты за перевозку однородного груза. А) Строим начальный план методом северо-западного угла. Составим таблицу значений:
Число назначенных перевозок m+n-1=3+5-1=7, то есть начальный план 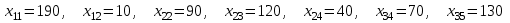 невырожденный. невырожденный.При таком плане суммарные транспортные издержки равны: 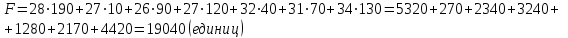 Б) Строим начальный план методом наименьшей стоимости. Составим таблицу значений:
Начальный план: 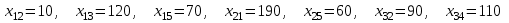 При таком плане транспортные издержки 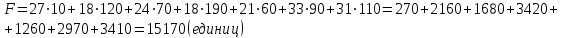 Сравнивая транспортные издержки, видим, что план, построенный методом наименьшей стоимости, лучший. 2. Выбираем лучший план и находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана: 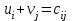
Используя первое условие оптимальности плана, составим систему линейных уравнений для определения потенциалов: 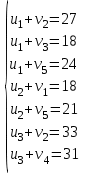 Система линейных уравнений содержит 7 уравнений и 8 неизвестных, т.е. она имеет множество решений. Так как нужно одно решение, то любой из неизвестных задаем значение и вычисляем остальные неизвестные. ■ Пусть 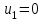 , тогда , тогда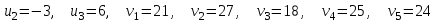 Проверяем второе условие оптимальности плана для свободных клеток 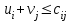 . Если есть нарушения, то заносим их со знаком «+». В результате проверки получили одну потенциальную клетку. Таким образом, начальный план не оптимален. . Если есть нарушения, то заносим их со знаком «+». В результате проверки получили одну потенциальную клетку. Таким образом, начальный план не оптимален.Улучшение плана. Выбираем клетку с максимальным нарушением и для нее строим замкнутый контур.
Среди клеток, помеченных знаком «-», выбираем наименьшую перевозку: 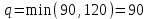 На эту величину увеличиваем перевозки в клетках, помеченных знаком «+», и уменьшаем в клетках, помеченных знаком «-». В результате переназначения перевозок имеем план:
Используя первое условие оптимальности плана, составим систему линейных уравнений для определения потенциалов: 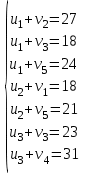 Система линейных уравнений содержит 7 уравнений и 8 неизвестных, т.е. она имеет множество решений. Так как нужно одно решение, то любой из неизвестных задаем значение и вычисляем остальные неизвестные. ■ Пусть 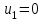 , тогда , тогда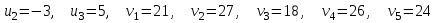 Проверяем второе условие оптимальности плана для свободных клеток 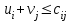 . Условие оптимальности выполнены, следовательно, план, соответствующий таблице, оптимален. . Условие оптимальности выполнены, следовательно, план, соответствующий таблице, оптимален.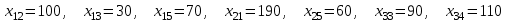 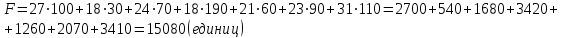 Ответ: Сравнивая три метода нахождения оптимального плана, делаем вывод, что метод потенциалов находит оптимальный план решения транспортной задачи, так как получили минимальные транспортные издержки равные 15080 единиц. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||