Теория вероятностей. Решение. Требуемую вероятность найдем с помощью классической формулы
 Скачать 13.88 Kb. Скачать 13.88 Kb.
|
|
1. В партии из 10 изделий 2 бракованных. Наугад выбирают три изделия. Определить вероятность того, что среди этих изделий будет хотя бы одно бракованное. 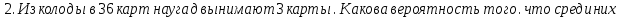 окажутся 2 туза? окажутся 2 туза?3. 12 рабочих получили путевки в 4 дома отдыха: 3 - в первый, 3 - во второй, 2 - в третий и 4 - в четвертый. Найти вероятность того, что данные трое рабочих поедут в один дом отдыха. 4. В магазин вошли 10 покупателей. Вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,2. Найти вероятность того, что 6 из них совершат покупку. 5. Вероятность изготовления изделия высшего качества равна 0,8. Найти вероятность того, что среди взятых 60 изделий 30 окажутся высшего качества. 6. В ящике 10 шаров: 6 красных и 4 белых. Из ящика вынимают сразу 4 шара. Найти вероятность того, что среди них 3 красных шара и 1 белый. 7. В партии из 10 изделий 8 стандартных. Найти вероятность того, что среди 2 наугад взятых изделий нет ни одного нестандартного. 8. Прибор содержит 3 независимо работающих устройства, поломка каждого из которых приводит к выходу из строя всего прибора. Вероятности выхода из строя каждого из этих устройств соответственно равны: 0,05, 0,15 и 0,2. Найти вероятность выхода из строя прибора. Образец выполнения контрольной. 1.В ящике 10 шаров: 7 черных и 3 белых. Из ящика вынимают 5 шаров. Найти вероятность того. что среди них окажется 3 черных и 2 белых шара. Решение. Требуемую вероятность найдем с помощью классической формулы: Число n - общее число возможных исходов - равно (поскольку порядок шаров безразличен) сочетанию 5 из 10 элементов: n = C Теперь определим число благоприятных исходов т. Очевидно, что способов, которыми можно вынуть 3 черных шара из 7 и 2 белых шара из 5 равно cсоответственно: С и С. Поскольку каждая комбинация черных шаров может сочетаться с любой комбинацией белых, всего получится С способов. Получим: Р(А) = Ответ: Р(А) ≈ 0,42 2.Из колоды в 36 карт наугад вынимают 5 карт. Какова вероятность того, что среди них не будет карты пиковой масти? Решение. Как и в предыдущем случае воспользуемся формулой классического подсчета вероятностей Очевидно, общее количество возможных исходов n равно С Так как в колоде 27 карт не пиково» масти, то благоприятным исходом можно считать извлечение 5 любых из них. Тогда m = С Получим: Р(А) = Ответ: Р(А) ≈ 0,214 3.Вероятность обнаружения опечатки на странице книги равна 0,01. Найти вероятность того, что в 500-страничной книге не будет обнаружено опечаток (обнаружение опечаток на различных страницах считать независимыми событиями). Решение. Поскольку в условиях независимых испытаний Бернулли вероятность р = 0,01 близка к нулю, а n = 500 велико, применим формулу Пуассона: Pn(k) = a=500 ∙ 0,01 = 5 Для k = 0 (отсутствие опечаток), получаем: H500(0) = Ответ: Р500 ≈ 0,007 4.Узел содержит три независимо работающие детали. Вероятность отказа деталей соответственно равны 0,1; 0,2; 0,3. Найти вероятность отказа учла, если для этого достаточно, чтобы отказала хотя бы одна деталь. Решение. Для нахождения вероятности события А - отказа узла, найдем сначала вероятность противоположного события Р(Ā), заключающегося в исправной работе всех деталей: Р(Ā) = (1-0,1)∙(1-0,2)∙(1-0,3) = 0,9∙0,8∙0,7 = 0,504. Искомая вероятность равна: Р(А) = 1 - Р(Ā) = 1-0,504 = 0,496 Ответ: Р(А) ≈ 0,496 Ну и всё в таком роде, формулы что то не копируются |
