9 класс повторение. Решение треугольника Истина ложь
 Скачать 208.44 Kb. Скачать 208.44 Kb.
|
|
Тема «Соотношение между сторонами и углами треугольника. Решение треугольника» «Истина – ложь» ( на предложенные высказывания учащиеся показывают ту карточку с буквой которую считают верной «И» - истина, «Л» - ложь) Треугольник это геометрическая фигура имеющая 3 стороны и 3 угла (И) Каждая сторона треугольника равна сумме двух других сторон (Л) В треугольнике против меньшего угла лежит большая сторона (Л) Площадь треугольника равна произведению его стороны на высоту проведенную к этой стороне (И) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними (Л) Верно ли выражение для данного треугольника 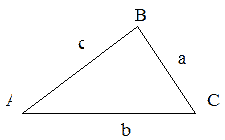  (Л) (Л)Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (И) 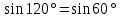 (И) (И)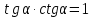 (И) (И)Решить треугольник значит найти угол и сторону этого треугольника. (Л) 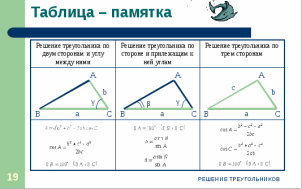 Решение задач на повторение. Задача 1: В треугольнике АВС АВ=0,6см, ВС=0,5см, 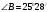 .Найдите сторону АС. .Найдите сторону АС. Решение Воспользуемся теоремой косинусов   3 группа: уровень А Задача 2: В треугольнике АВС АВ=10см,  . Найдите сторону АС. . Найдите сторону АС.  Решение РешениеВоспользуемся теоремой синусов: 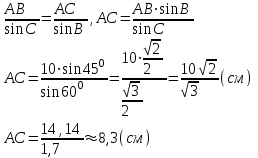  Ответ:8,3 см Ответ:8,3 смЗадача 3: Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и стоек ворот. Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м. Решение: Решим треугольник АВС(задача 1) и найдем угол А, равный α По теореме косинусов определим cos А 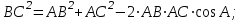  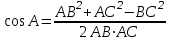 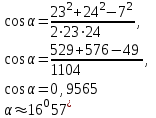 Ответ: 16057/ Задача 4: Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить. Основание башни он видит под углом 2° к горизонту, а вершину — под углом 45° к горизонту. Какова высота башни? Дано: АВ=50 м, BDH=20, CDH=450, DH||AB. Найти: СВ Решение   DH || AB → DH || AB → BDH= BDH= DBA=20, как накрест лежащие. DBA=20, как накрест лежащие.cos  DBA= DBA= ДВ= ДВ=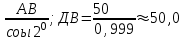 Применим терему синусов: ΔСDB: 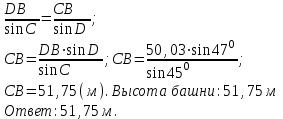 Задача 5. Две стороны треугольника имеют длины 6см и 12 см, а угол между ними равен 1200. Найдите длину биссектрисы, проведенной к большей стороне. Решение П  усть дан треугольник АВС:АВ=6 см, ВС=12 см, усть дан треугольник АВС:АВ=6 см, ВС=12 см, 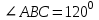 .Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем: .Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем: cos 1200= cos 1200=36 + 144 - 2  6 6 12 12 (-0,5) = 252; AC = (-0,5) = 252; AC = 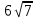 (см) (см)Задача 6: Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o - с другой. Найти длину скатов крыши с точностью до сантиметра. Решение 1  )Угол крыши )Угол крыши 2)По теореме синусов 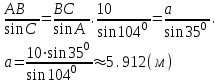 3)По теореме синусов: 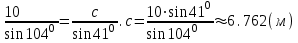 Ответ: 5,912 см; 6,762 м. |
