ответы. ОТвет9. Решение у куба 6 граней. На каждой грани расположено 1010100 квадратов, которые являются основаниями маленьких кубиков
 Скачать 34.48 Kb. Скачать 34.48 Kb.
|
|
1.1 СЛУЧАЙНЫЕ СОБЫТИЯ 9. Куб, все грани которого окрашены, распилен на тысячу кубиков одного размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три Решение У куба 6 граней. На каждой грани расположено 10·10=100 квадратов, которые являются основаниями маленьких кубиков. С тремя окрашенными гранями 8 кубиков , они расположены в 8–ми вершинах куба. Кубики, имеющие 2 окрашенные грани, находятся на ребрах куба и не совпадают с вершинами. На одном ребре куба находится 10 кубиков. 2 кубика в углах – вершины, они имеют по три окрашенные грани, значит 10–2=8 кубиков имеют по две окрашенные грани. У куба 12 ребер, следовательно, всего таких кубиков 12·8=96 штук. Одну окрашенную грань имеют кубики, которые лежат на грани, но не лежат на ребре. Таких кубиков на одной грани 100– 8·4–4=64 На 6 гранях лежат 64·6= 384 кубика с одной окрашенной гранью. Следовательно: 1) р=384/1000=0,384 вероятность того, что на удачу извлечённый кубик имеет 1 окрашенную грань; 2) p=96/1000=0,096 вероятность того, что на удачу извлечённый кубик имеет 2 окрашенные грани; 3) р=8/1000 = 0,008 вероятность того, что на удачу извлечённый кубик имеет 3 окрашенные грани. О т в е т. 1) 0,384; 2)0,096; 3)0,008 1.2. СЛУЧАЙНЫЕ СОБЫТИЯ 9.Вероятность того, что в течение смены станок выйдет из строя равна 0,05. Найти вероятность того, что в течение трех смен станок будет работать исправно. Вероятность, что неполадка не произойдет: 1 - 0,05 = 0,95 P(не произойдет неполадка в течение трех смен) = 0,95 * 0,95 * 0,95 = 0,857375 2.СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 9. Два стрелка поочередно стреляют по мишени. Вероятность промаха для первого стрелка равна 0,2; для второго 0,4. Произведено не более 4 выстрелов. Составьте закон распределения дискретной величины X - числа выстрелов, произведенных до первого попадания. Решение: р0=0.2*0,2*0,4*0,4=0.0064 – вероятность того, что оба стрелка промазали различная вероятность случайных событий того, что один стрелок промазал, другой попал в 4 выстрелах:р1,р2,р3 р1=0,8*0,2*0,6*0,6+0,2*0,8*0,6*0,6+0,2*0,8*0,4*0,6+0,8*0,2*0,6*0,4=0,192 – p2=0,8*0,8*0,6*0,6+0,2*0,8*0,4*0,6+0,2*0,8*0,6*0,4+0,8*0,2*0,4*0,6+0,8*0,2*0,6*0,4+0,8*0,8*0,4*0,4=0,4864 p3=0,8*0,8*0,4*0,6+0,2*0,2*0,4*0,4+0,2*0,8*0,4*0,4+0,8*0,2*0,6*0,4=0,224 p4=0.8*0,8*06*0,6=0,2304– Вероятность того, что оба стрелка попали Окончательно, закон распределения дискретной величины Х имеет вид:
3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 9. X и У - независимые случайные величины D(X) = 4, D(У) = 5. Найти дисперсию случайной величины Z = ЗХ + ЗУ. Решение. Так как величины X и Y независимы, то независимы также и величины 3X и 3Y. Используя свойства дисперсии получим: D(Z)=D(3X+3Y)=D(3X)+D(3Y)=9D(X)+9D(Y)=9*4+9*5=81 4. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 9.Постройте полигон частот xi 15 20 25 30 10 ni 10 15 30 20 25 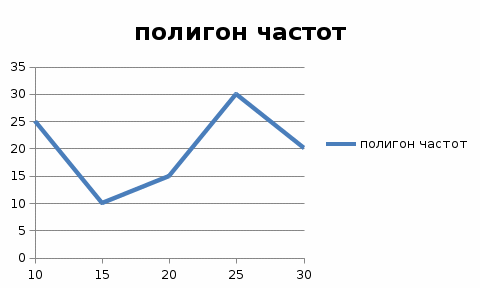 |
