24 задачи. Решение Угловое ускорение найдем из кинематического уравнения отсюда Угловая скорость и частота оборотов связаны соотношением
 Скачать 476.88 Kb. Скачать 476.88 Kb.
|
|
24 задачи Контрольная работа №1 101. Маховик начал вращаться равноускоренно и за промежуток времени Δt = 10 c достиг частоты вращения п = 300 мин‾ ¹. Определить угловое ускоре ние маховика и число N оборотов, которое он сделал за это время.
Решение: Угловое ускорение найдем из кинематического уравнения 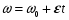 отсюда отсюда 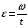 Угловая скорость и частота оборотов связаны соотношением 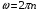 Тогда угловое ускорение равно 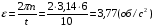 Полный угол поворота при равноускоренном движении находится из соотношения: φ = ω0 t+ 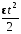 , ,где φ =2π N; ω0=0, тогда 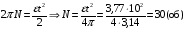 Ответ: ε=3,77об/с2; N= 30 оборотов. 112. Шар массой m = 1,8 кг сталкивается с покоящимся шаром большей массы М. В результате прямого, центрального, абсолютно упругого удара шар потерял w = 0,36 своей кинетической энергии. Определить массу М большего шара.
Решение: 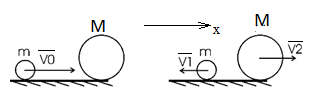 Применим закон сохранения импульса: 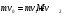 Проецируя на ось х: 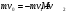 Применим закон сохранения энергии: 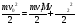 . .Выразим потерю кинетической энергии первого шара: 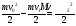 Учитывая, что шар потерял 36% своей энергии: 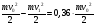 . .Тогда, 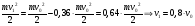 . .С другой стороны 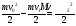 и и 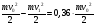 , следовательно, , следовательно, 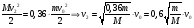 Подставляя в уравнения импульса, получим: 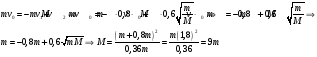 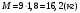 Ответ: М=16,2 кг 122. Какая работа А должна быть совершена при поднятии с земли ма териалов для постройки цилиндрической дымоходной трубы высотой h = 40 м. наружным диаметром D = 3 м и внутренним диаметром d = 2 м? Плотность материала принять равной 2800 кг/м3.
Решение: 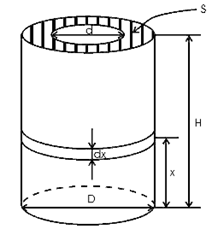 Найдем потенциальную энергию тонкого слоя dx, находящегося на высоте х (см рис.). Для этого нам нужно узнать массу этого слоя: 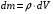 , , где ρ – плотность материала, 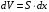 - объем этого слоя. - объем этого слоя.Тогда масса слоя 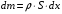 Отсюда потенциальная энергия равна 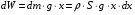 Проинтегрируем правую и левую части: 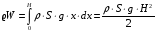 Площадь кольца (см рис) вычислим как 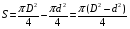 Потенциальная энергия установки трубы равна совершенной работе, тогда 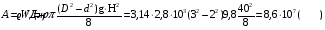 Ответ: А= 86 МДж. 132. По горизонтальной плоскости катится диск со скоростью υ = 8 м/с. Определить коэффициент сопротивления f, если диск, будучи предоставлен ным самому себе, остановился, пройдя путь S = 18 м.
Решение: 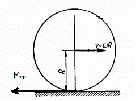 Момент M силы F относительно какой-нибудь оси вращения определяется формулой M=Fl, где l – кратчайшее расстояние от прямой, вдоль которой действует сила, до оси вращения, оно равно радиусу цилиндра Тогда момент силы трения будет равно 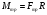 (1) (1)С другой стороны диск останавливается под действием сил трения, поэтому на него действует момент сил трения все время до остановки. Момент сил находится по формуле: Mтр =Jε. (2) где 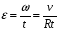 - угловое ускорение (4) - угловое ускорение (4)Подставим (4) и (3) в (2) и приравняем к (1) получим 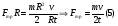 С другой стороны сила трения по определению 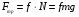 До остановки диск проходит путь 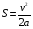 , а модуль ускорения этого диска , а модуль ускорения этого диска 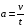 , тогда подставим все это в (5) и выразим искомую величину , тогда подставим все это в (5) и выразим искомую величину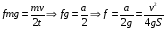 Подставим числовые значения, получим 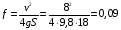 Ответ: f=0,09 142. Какой наибольшей скорости υ может достичь дождевая капля диа метром d = 0,3 мм, если динамическая вязкость воздуха = 1,2·10-5 Па·с?
Решение: 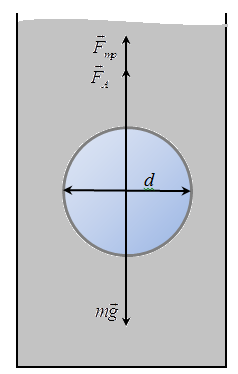 Согласно закону Ньютона, сила внутреннего трения между слоями определяется формулой: где η – коэффициент вязкости; S – площадь поверхности, к которой приложена сила. На движущуюся каплю действуют три силы: 1.Сила тяжести где r – радиус капли; ρ2 – плотность капли (плотность воды); g – ускорение силы тяжести.
здесь ρ1 – плотность воздуха. (Силу Архимеда, ввиду малости можно не учитывать). 3.Сила внутреннего трения (сила сопротивления движения капли). Эта сила также направлена против движения капли. Стокс на основании теоретических исследований установил, что если шарик движется в жидкости, не вызывая при своем движении никаких завихрений, то сила сопротивления движения шарика определяется формулой где Следует учесть, что при движении шарика имеет место не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как шарик обволакивается тонким слоем жидкости, и этот слой жидкости движется вместе с шариком. Сила трения с увеличением скорости движения капли возрастает, следовательно, при движении капли скорость её может достигнуть такой величины, при которой все три силы, действующие на каплю, будут уравновешены, то есть равнодействующая их будет равна нулю. Такое движение капли будет равномерным, и капля будет двигаться по инерции с постоянной скоростью. Уравнение динамики для такого движения будет: 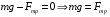 или 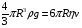 Откуда скорость капли: 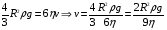 Подставим числовые значения, получим: 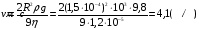 Ответ: v=4,1 м/с 152. Определить скорость υ, при которой релятивистский импульс час тицы превышает ее ньютоновский импульс в n = 3 раза.
Решение: Релятивистский импульс равен: 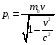 Где с=3·108 м/с – скорость света Ньютоновский импульс 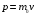 , по условию задачи р1=3р, тогда , по условию задачи р1=3р, тогда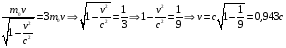 Ответ: v=2,83·108 м/с. 162. Тело массой т = 4 кг, закрепленное на горизонтальной оси, совер шало колебания с периодом Т1 = 0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период T2 колебаний стал равным 1,2 с. Радиус R диска равен 20 см, масса его равна массе тела. Найти момент инерции J тела относительно оси колебаний.
Решение: Период колебаний физического маятника определяется по формуле: 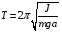 , где J – момент инерции системы колеблющихся тел, относительно оси колебаний, m – масса системы, а – расстояние между центрами тяжести самой системы и осью колебаний. После того, как на ось насадили диск, момент инерции системы изменится и его определяют с помощью уравнения , где J – момент инерции системы колеблющихся тел, относительно оси колебаний, m – масса системы, а – расстояние между центрами тяжести самой системы и осью колебаний. После того, как на ось насадили диск, момент инерции системы изменится и его определяют с помощью уравнения 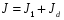 , где , где 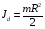 - момент инерции диска - момент инерции дискаЗапишем период колебаний тела без диска и с диском 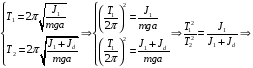 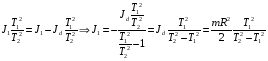 Подставим числовые значения, получим 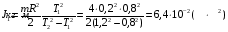 Ответ: J1=6,4∙10-2 кг∙м2 172. Определить длину λбегущей волны, если в стоячей волне расстоя ние lмежду первой и седьмой пучностями равно 15 см.
Решение: 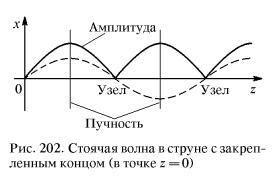 Длина стоячей волны (см рис) 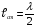 , где λ – длина волны колебаний. С другой стороны , где λ – длина волны колебаний. С другой стороны 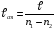 где n1 и n2 – порядковые номера пучностей или узлов. Тогда приравнивая эти два выражения получим: где n1 и n2 – порядковые номера пучностей или узлов. Тогда приравнивая эти два выражения получим: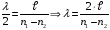 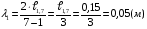 Ответ: λ=5 см; Контрольная работа №2 201. В колбе вместимостью V = 100 см3 содержится некоторый газ при температуре Т= 300 К.. На сколько понизится давление р газа в колбе, если вследствие утечки из колбы выйдет N=1020 молекул?
Решение: Для решения задачи воспользуемся уравнением Менделеева – Клайперона в виде 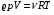 , где ∆р – искомое понижение давления; , где ∆р – искомое понижение давления; R - газовая постоянная υ –количество вещества, которое найдем, используя связь с количеством молекул 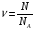 , где NА – число Авогадро , где NА – число АвогадроСовместит оба выражения, получим 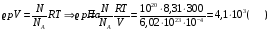 Ответ: давление понизится на 4,1 кПа. 211. На какой высоте h над поверхностью Земли атмосферное давление вдвое меньше, чем на ее поверхности? Температуру Т воздуха, равную 290 К, и ускорение g свободного падения считать независящими от высоты.
Логарифмирование выражения (1) дает 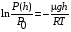 . (2) . (2) Из соотношения (2) находим высоту h: 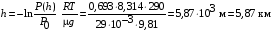 . .Ответ: h = 5,87 км. 221. Найти среднюю продолжительность <τ> свободного пробега моле кул кислорода при температуре Т = 250К и давлении р = 100 Па.
Решение: Средняя длина свободного пробега молекул определяется концентрацией n по формуле 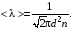 (1) (1) где d=2,9·10-10 – эффективный диаметр молекулы , n – концентрация молекул кислорода. Средняя продолжительность свободного пробега молекул < τ > имеет вид 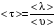 (2) (2)концентрация молекул n может быть вычислена из формулы: 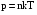 откуда 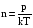 (3) (3)Постоянная Больцмана k связана с числом Авогадро NA соотношением: 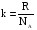 (4) (4)Средняя арифметическая скорость молекул газа равна 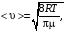 (5) (5)где R – универсальная газовая постоянная. Тогда с учетом (3) и (4) средняя длина свободного пробега 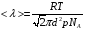 Средняя продолжительность свободного пробега молекул рассчитаем учитывая (5) 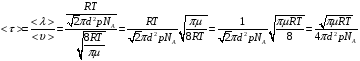 Подставим числовые значения, получим 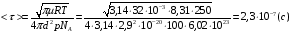 Ответ: < τ>=2,3·10-7 с 231. Газовая смесь состоит из азота массой т1 = 3 кг и водяного пара массой т2 = 1 кг. Определить удельные теплоемкости cv и сp, газовой смеси.
Если нагревание происходит при постоянном объеме, то: 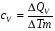 , где , где 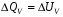 , т.е. все сообщаемое количество теплоты идет на изменение внутренней энергии системы. Изменение внутренней энергии смеси газа определяется формулой: , т.е. все сообщаемое количество теплоты идет на изменение внутренней энергии системы. Изменение внутренней энергии смеси газа определяется формулой: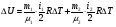 , где i1 и i2 – число степеней свободы первого и второго газов. Для молекулы водяного пара , где i1 и i2 – число степеней свободы первого и второго газов. Для молекулы водяного пара Окончательно получим: 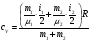 . (1) . (1)Произведем вычисления: 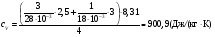 Если нагревание происходит при постоянном давлении, то 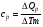 , (2) , (2) где 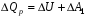 , т.е. сообщаемое газу количество теплоты идет не только на изменение внутренней энергии, но и на работу по расширению газа. Работа при изобарическом расширении для каждого газа равна: , т.е. сообщаемое газу количество теплоты идет не только на изменение внутренней энергии, но и на работу по расширению газа. Работа при изобарическом расширении для каждого газа равна: 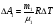 ; ; 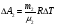 , поэтому: , поэтому: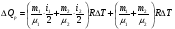 . .Подставляя это значение в уравнение (2), получим: 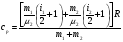 . .Произведем вычисления: 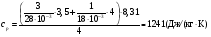 Ответ: Сv =901 Дж/кг·К; Ср =1241 Дж/кг·К; 241. Водород занимает объем V= 10 м3 при давлении p1 = 100 кПа. Газ нагрели при постоянном объеме до давления p2 = 300 кПа. Определить: 1) из менение ∆U внутренней энергии газа; 2) работу А, совершенную газом; 3) количество теплоты Q, сообщенное газу.
Решение: Работа газа при изохорном расширении  А=0. А=0.Изменение внутренней энергии газа определяется изменением его температуры: 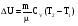 , ,где: 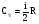 – молярная теплоемкость газа при постоянном объеме, i – число степеней свободы молекулы (водород –двухатомный газ, поэтому i = 5). – молярная теплоемкость газа при постоянном объеме, i – число степеней свободы молекулы (водород –двухатомный газ, поэтому i = 5). Из уравнения Менделеева - Клайперона: 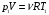 , , 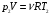 , ,поэтому: 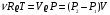 Тогда: 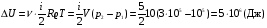 . .На основании первого начала термодинамики определим теплоту, полученную газом: 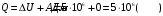 . .Ответ: А=0; ∆U=5МДж; Q=5МДж. 251.Идеальный газ, совершающий цикл Карно, получив от нагревателя количество теплоты Q1 = 4,2 кДж, совершил работу А = 590 Дж. Найти тер мический КПД η этого цикла. Во сколько раз температура Т1 нагревателя больше температуры Т2 охладителя?
Решение: Воспользуемся теоремой Карно: коэффициент полезного действия (к. п. д.) 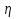 тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя 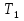 и холодильника и холодильника 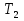 и не зависит от природы рабочего тела и устройства тепловой машины и не зависит от природы рабочего тела и устройства тепловой машины 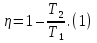 К. п. д. цикла Карно можно записать также через работу 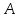 и тепло и тепло 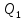 , переданное рабочему телу от нагревателя: , переданное рабочему телу от нагревателя: 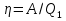 , , Приравняем (1) и (2) и выразим искомую величину 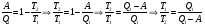 Подставим числовые значения, получим  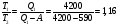 Ответ:  261. Какую работу А нужно совершить, чтобы, выдувая мыльный пу зырь, увеличить его диаметр от d1 = 1 см до d2 = 11 см? Процесс считать изо термическим.
Решение: Работа которую надо совершить при выдувании мыльного пузыря равна изменению энергии поверхностного натяжения, которая выражается формулой: 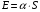 , , где – α=0,04 Н/м - коэффициент поверхностного натяжения мыльной пленки, S - полная площадь поверхности пленки, которая равна: 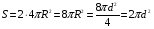 Здесь учитывается внешняя и внутренняя поверхности. Тогда работа будет равна: 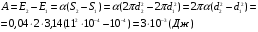 Ответ: А=3 мДж. 271. Вычислить постоянные а и b в уравнении Ван-дер-Ваальса для ксе нона. Критическую температуру Ткр и критическое давление ркр для ксенона считать известными.
Решение: Уравнение Ван-дер-Ваальса имеет вид 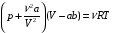 Постоянные а и b из уравнения Ван-дер-Ваальса выражаются соотношениями: 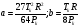 где R=8,31Дж/моль·К – газовая постоянная 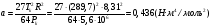 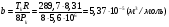 Ответ: а=0,436 Н·м4/моль2; b=5,37·10-5 м3/моль Контрольная работа №3 301. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики по гружаются в керосин. Определить диэлектрическую проницаемость ε керо сина, если угол расхождения нитей при погружении шариков в керосин оста ется неизменным. Плотность материала шариков ρ = 1600 кг/м3.
Решение: 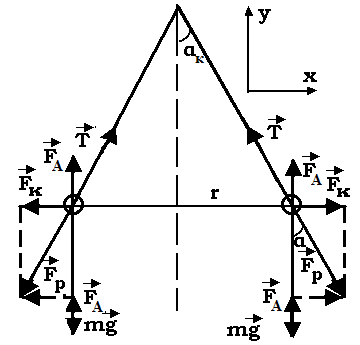 На каждый шарик действуют четыре силы: сила тяжести, сила Кулона, сила натяжения нити и сила Архимеда. Т.к. шарики находятся в положении равновесия, то сумма этих сил равна нулю. Проекции на выбранные оси координат Сила Кулона Сила натяжения нити По закону Кулона Заряд каждого шарика будет равен половине суммарного заряда Расстояние между зарядами Тогда Масса шарика будет равна Выражаем массу через плотность и расписываем силу Архимеда И подставляем в (1) 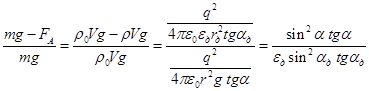 Тогда плотность материалов шариков 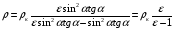 Отсюда диэлектрическая проницаемость керосина равна 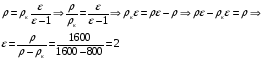 Ответ: ε=2 311. На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = 120 нКл/м2 и σ2 = 30 нКл/м2 (рис. 1). Используя теорему Остроградского – Гаусса, найти зави симость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от центра на расстояние r = 1,5R, и указать направление вектора Е. Построить график зависимости Е(r).
Решение: 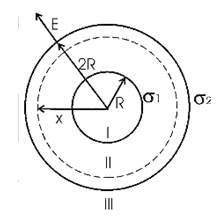 Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рисунок 1): области 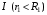 , области , области 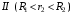 , области , области 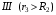 . .1. Для определения напряженности 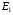 в области I проведем гауссову поверхность в области I проведем гауссову поверхность 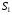 радиусом r1 и воспользуемся теоремой Остроградского–Гаусса: радиусом r1 и воспользуемся теоремой Остроградского–Гаусса: 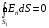 (т. к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии (т. к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии 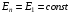 . Следовательно, . Следовательно, 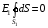 и и 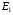 (напряженность поля в области I) во всех точках, удовлетворяющих условию (напряженность поля в области I) во всех точках, удовлетворяющих условию 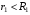 , будет равна нулю, т. е. Е1 = 0. , будет равна нулю, т. е. Е1 = 0.2. 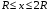 В области II гауссову поверхность проведем радиусом r2. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум)): В области II гауссову поверхность проведем радиусом r2. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум)): 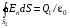 , (1) , (1)(т. к. внутри гауссовой поверхности находится только заряд 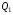 ). Из соображения симметрии ). Из соображения симметрии 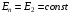 , то Е можно вынести за знак интеграла: , то Е можно вынести за знак интеграла: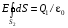 , или , или 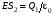 . (2) . (2)Обозначив напряженность Е для области II через 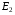 , а заряд , а заряд 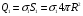 получим получим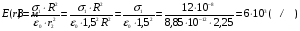 (3) (3)3. 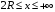 .В области III гауссова поверхность проводится радиусом r3. Обозначим напряженность Е области III через Е3 и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен .В области III гауссова поверхность проводится радиусом r3. Обозначим напряженность Е области III через Е3 и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен 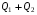 . Тогда . Тогда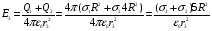 . . График зависимости E(r) от r изобразим в виде: 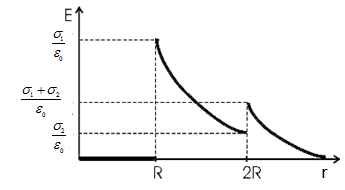 Ответ: E2=6 кВ/м 321. Сто одинаковых капель ртути, заряженных до потенциала φо = 20 В, сливаются в одну большую каплю. Каков потенциал φ образовавшейся кап ли?
Решение: Выразим радиус большой капли (R) капли через радиус малой r. Для этого воспользуемся тем фактом, что суммарный объем не изменится 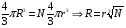 (1) (1)Суммарный заряд тоже не изменится и его найдем как 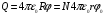 Отсюда потенциал образовавшейся капли 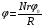 Тогда с учетом (1) получим 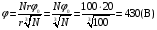 Ответ: φ=430 В. 331. В плоский воздушный конденсатор вдвинули плитку парафина тол щиной h = 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние d между пластинами, чтобы получить прежнюю емкость?
Решение: Начальная емкость плоского воздушного конденсатора вычисляется по формуле: 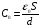 После раздвижения пластин емкость конденсатора найдем как емкость двух конденсаторов С1 и С2. Емкость двух последовательно соединенных конденсаторов вычислим по формуле: 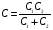 , где С1=εС0, , где С1=εС0, 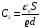 . .По условию С0=С т.е. 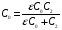 или после преобразования или после преобразования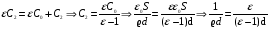 Отсюда 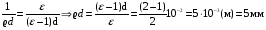 Ответ: ∆d=5 мм. 341. При силе тока I1 = 3 А во внешней цепи батареи аккумуляторов вы деляется мощность Р1 = 18 Вт, а при силе тока I2 = 1 А – соответственно мощность Р2 = 10 Вт. Определить ЭДС ξ и внутреннее сопротивление rба тареи.
Решение: Из формулы мощности выразим и рассчитаем внешнее сопротивление для обоих случаев 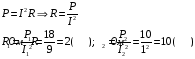 Закон Ома для полной цепи: 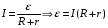 Запишем это выражение для двух случаев 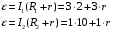 Приравняв эти выражения друг к другу выразим и найдем внутреннее сопротивление 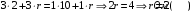 Подставив значение внутреннего сопротивления в закон Ома найдем ЭДС 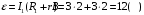 Ответ: Ԑ=12 В, r=2Ом. 351. Две батареи аккумуляторов с ЭДС ξ1 = ξ2 = 100 В и четыре резисто ра с сопротивлениями R1 = 20 Ом, R2 = 10 Ом, R3 = 40 Ом и R4 = 30 Ом со единены, как показано на рис. 1. Найти показание IA амперметра. Внутрен ними сопротивлениями r, батарей аккумуляторов пренебречь.
Решение: 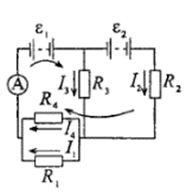 Выберем и рассмотрим два контура, для каждого из них выберем направление обхода по часовой стрелке (см рис.) Предположительно определим направление токов в каждом сопротивлении. Для каждого контура запишем уравнение по второму правилу Кирхгофа 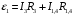 (1) (1)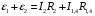 (2) (2)Сопротивления 1 и 4 соединены параллельно, поэтому их общее сопротивление 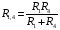 (3) (3)Согласно первому закону Кирхгофа 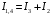 (4) где (4) где 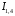 - ток, котрый покажет амперметр. - ток, котрый покажет амперметр.Из уравнений (1) и (2) находим токи 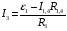 и и 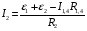 И подставляем их в уравнение (4), тогда 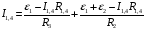 , учтем (3) и окончательно получим , учтем (3) и окончательно получим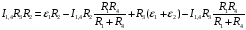 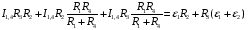 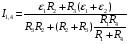 Подставим числовые значения, получим 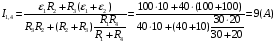 Ответ: амперметр показывает силу тока 9 А. 361. Определить суммарный импульс р электронов в прямом проводе длиной l = = 500 м, по которому течет ток I= 20 А.
Решение: Импульс одного электрона равен 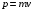 , где m=9,1·10-31 кг – масса одного электрона. , где m=9,1·10-31 кг – масса одного электрона.Импульс всех электронов 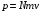 Среднюю скорость электронов найдем из формулы плотности тока 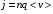 , где q=1,6·10-19 Кл – заряд электрона; , где q=1,6·10-19 Кл – заряд электрона; 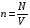 - концентрация частиц в заданном объеме; - концентрация частиц в заданном объеме; 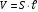 Плотность тока по определению 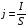 Объединим все формулы 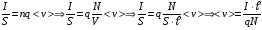 Суммарный импульс рассчитаем как 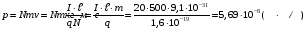 Ответ: р=5,69·10-8 кг·м/с. 371. При электролизе медного купороса (CuS04) в течение времени t = 1 ч при силе тока I = 1 А на катоде выделилась медь массой т = 1,66 г. Определить коэффициент полезного действия η установки.
Решение: 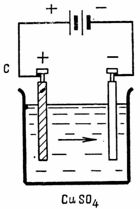 Для электролиза справедливы два закона Фарадея I закон Фарадея: Масса вещества, выделившегося при электролизе, с учетом кпд установки 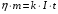 где К =0,33·10-6 кг/Кл – электрохимический эквивалент меди; Отсюда кпд установки 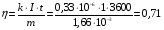 Ответ: η=0,71 |

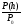 = 0,5
= 0,5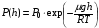 , (1)
, (1) 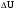 =?
=?