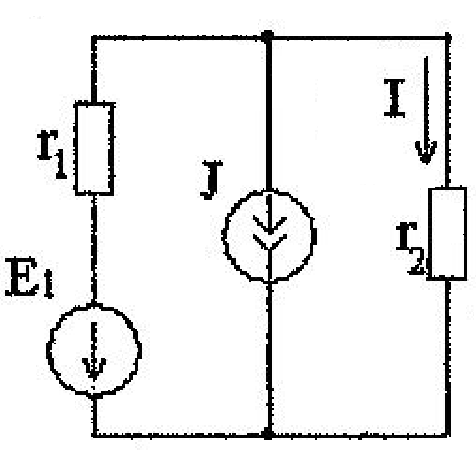
119413_Решение. Решение Укажем на схеме направления токов, ток первой ветви обозначим через (рис. 2)
 Скачать 398 Kb.
|
|
Вариант № 17 1 Определить ток I в схеме (рис. 1.1), применив метод наложения.
Исходные данные:  ;  ;  ;  .Решение Укажем на схеме направления токов, ток первой ветви обозначим через  (рис. 1.2).
Определяем частичный ток  . Выполним расчет цепи при воздействии источника ЭДС  , полагая  . Источники считаем идеальными, поэтому внутреннее сопротивление ЭДС равно нулю, а источника тока – бесконечности. С учётом этого изобразим расчетную схему (рис. 1.3).
 .Определяем частичный ток  . Выполним расчет цепи при воздействии источника тока  , полагая  . Расчетная схема (рис. 1.4).
 .Ток в первой ветви исходной схемы (рис. 1.1) от действия источника ЭДС и источника тока определим, как алгебраическую сумму частичных токов:  .Знак «минус» означает, что истинное направление тока  противоположно направлению, показанному на рис. 1.1.Для проверки рассчитаем ток в третьей ветви схемы методом узловых потенциалов. Примем потенциал одного из узлов равным нулю (  ). Определяем проводимости ветвей:  ; ; ; .Произвольно выбираем положительное направление напряжения  между узлами и записываем в соответствии с формализованным правилом расчетное выражение для определения межузлового напряжения.   Ток в ветви равен алгебраической сумме действующей в ветви ЭДС и межузлового напряжения, умноженной на проводимость этой ветви:  .Ответ:  .2 Известно, что в последовательном колебательном контуре (рис. 2.1) при резонансной частоте  отношение напряжения на ёмкости к напряжению на входе равно 50. Емкость  . Вычислить  и  контура.
Решение Резонанс возможен при совпадении фаз входного напряжения и тока. Так как участки цепи, содержащие емкость и индуктивность соединены последовательно, в этом случае возникает резонанс напряжений (рис. 2.1). Входное сопротивление цепи.  Преобразуем полученное выражение и выделим действительную и мнимую части:  При резонансе мнимая часть входного сопротивления приравнивается к нулю:  ; Отсюда  С учётом того, что  , имеем: .Вычислим:  .Сопротивление на емкости:  Обозначим через I ток в цепи. Тогда входное напряжение:  При резонансе напряжений , поэтому  .Напряжение на емкости  По условию, 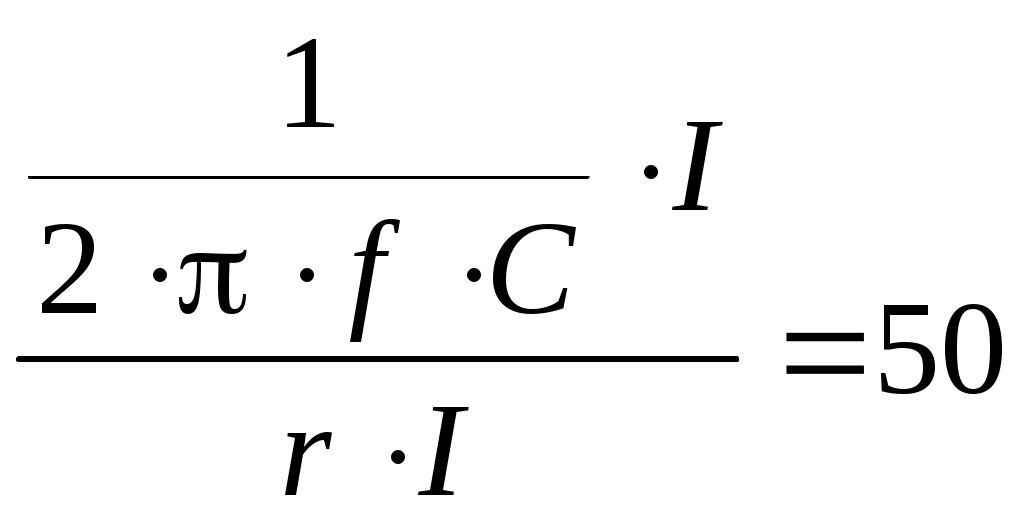 , то есть или  Отсюда  Вычислим:  Ответ:  ,  . |
