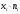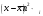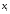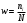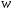Решение Уравнение линейной регрессии с y на x имеет вид Выборочные средние
 Скачать 152.15 Kb. Скачать 152.15 Kb.
|
|
Вариант 11 Задание 1 Найти линейное уравнение регрессии 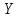 на на  по приведенной корреляционной таблице. Используя полученное значение, вычислить оценку среднего значения случайной величины по приведенной корреляционной таблице. Используя полученное значение, вычислить оценку среднего значения случайной величины 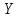 при при  . ( . ( - абсолютная частота появления в выборке пары случайных величин - абсолютная частота появления в выборке пары случайных величин  ). ).
Решение Уравнение линейной регрессии с Y на X имеет вид:  Выборочные средние:   Несмещенные оценки дисперсии:  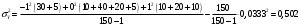 Тогда среднеквадратические отклонения будут:  и и  Рассчитаем ковариацию: 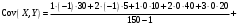 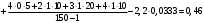 Определим коэффициент корреляции: 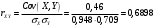 Тогда искомое уравнение регрессии будет иметь вид:  Преобразуем и получим: 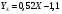 Вычислить оценку среднего значения случайной величины 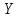 при при 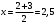 . . Задание 2 Наблюдения за дискретной случайной величиной заданы в виде упорядоченной выборки, представленной в таблице. В первой строке указаны выборочные значения  случайной величины, во второй абсолютные частоты случайной величины, во второй абсолютные частоты  появления соответствующих значений в выборке. появления соответствующих значений в выборке.Требуется: построить полигон относительных частот: построить график эмпирической функции распределения случайной величины, вычислить выборочное среднее, выборочную дисперсию и выборочное среднее квадратическое отклонение случайной величины. найти размах варьирования, моду и медиану.
Решение Находим относительные частоты по формуле  , а также накопленные относительные частоты , а также накопленные относительные частоты  . .
Полигон относительных частот: 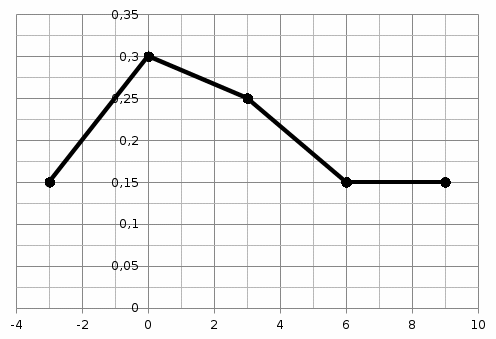 Функция распределения 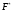 имеет вид: имеет вид: График функции распределения имеет вид:  Для расчета остальных показателей составляем расчетную таблицу:
Выборочная средняя: 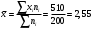 Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Максимальное значение повторений при   . Следовательно, мода равна 0. . Следовательно, мода равна 0. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим 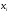 , при котором накопленная частота S будет больше , при котором накопленная частота S будет больше  . Это значение . Это значение  . Таким образом, медиана равна 3. . Таким образом, медиана равна 3. Дисперсия: 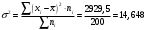 Среднее квадратическое отклонение.  Каждое значение ряда отличается от среднего значения 3 в среднем на 3,827. Задание 3 Произведено  наблюдений над непрерывной случайной величиной наблюдений над непрерывной случайной величиной  . Диапазон изменения величины разбит на 6 отрезков . Диапазон изменения величины разбит на 6 отрезков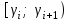 . Отрезки и число наблюдений . Отрезки и число наблюдений  , попавших в каждый из них, приведены в таблице. Требуется: , попавших в каждый из них, приведены в таблице. Требуется:построить гистограмму относительных частот; построить график эмпирической функции распределения: вычислить выборочное среднее, выборочную дисперсию и выборочное среднее квадратическое отклонение.
Решение Составляем расчетную таблицу
Гистограмма относительных частот: 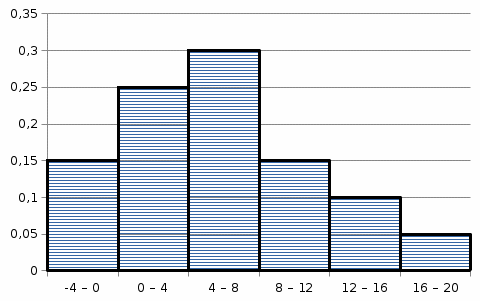 Функция распределения 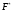 имеет вид: имеет вид: График эмпирической функции распределения: 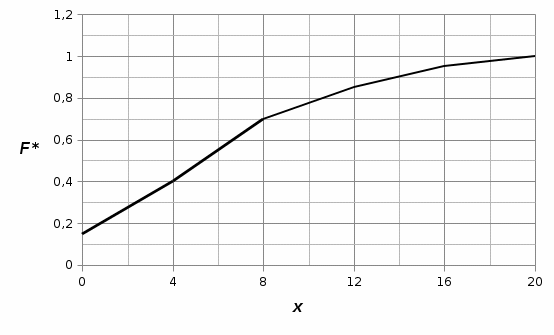 Выборочная средняя: 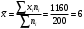 Дисперсия:  Среднее квадратическое отклонение.  Каждое значение ряда отличается от среднего значения 6 в среднем на 5,437. Список литературы Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2010. – 311 с. Математика для экономистов: от арифметики до эконометрики : учеб.-справ. пособие для бакалавров / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман ; под ред. Н. Ш. Кремера. – 3-е изд., перераб. и доп. – М. : Юрайт, 2012 . – 685 с. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2007. – 344 с. Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. – Казань: ТИСБИ, 2005. – 56 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1
1 2
2 3
3 4
4 -1
-1 30
30 5
5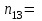 0
0 0
0 0
0 10
10 40
40 20
20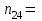 5
5 1
1 0
0 10
10 20
20 10
10