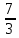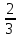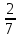|
|
Самостоятельные работы по алгебре 7 класс(Дорофеев В.Г. САМОСТОЯТЕЛЬНЫЕ РАБОТЫ ПО АЛГЕБРЕ 7 КЛАСС(ДОРОФЕЕВ). Решение уравнений, Преобразование выражений, Многочлены
Самостоятельные работы для 7 класса
|
Описание работы
Работа содержит три самостоятельные работы для 7 класса по темам «Решение уравнений», «Преобразование выражений», «Многочлены». Задания, составленные на основе стабильного учебника алгебры для 7 класса (авторы Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и другие). Каждая работа содержит восемь вариантов по шесть заданий в каждом различного уровня сложности.
|
Технологическая карта контрольно-измерительных материалов
Класс
|
7
|
Предмет
|
Алгебра
|
Учебник, по которому ведется преподавание
|
Алгебра Г.В.Дорофеев, С.Б.Суворова, Е.А.Бунимович и др. Учебник для 7 класса. «Просвещение», 2014
|
Статус дидактических материалов
|
Дидактические материалы являются авторскими
|
Тема контроля
|
Решение уравнений, преобразование выражений, многочлены.
|
Вид контроля
|
Тематический
|
Формы и методы контроля
|
Индивидуальная письменная работа
|
Тип контроля
|
Внешний
|
Время контроля
|
20 мин
|
Цель контроля
|
Выявить типичные ошибки, обратить на них внимание учащихся.
|
Содержание контроля
|
Работы содержат 8 вариантов по 6 заданий в каждом разного уровня сложности
|
Критерии контроля
|
Отметка «5» выставляется, если объем работы, выполняемый учеником без ошибок, составляет от 99% до 100%
Отметка «4» выставляется, если объем работы, выполняемый учеником без ошибок, составляет от 75% до 99%
Отметка «3» выставляется, если объем работы, выполняемый учеником без ошибок, составляет от 50% до 75%
Отметка «2» выставляется, если объем работы, выполняемый учеником без ошибок, составляет менее 50%
|
Самостоятельные работы
по алгебре для 7 класса
Пояснительная записка
Самостоятельная работа в обучении математике необходима для перевода знаний извне во внутреннее достояние учащегося, необходима для овладения этими знаниями, а также для осуществления контроля со стороны учителя за их усвоением.
Содержание самостоятельных работ определяется на ряд принципов:
1. соответствие содержания работы целям контролирования;
2. определение значимости проверяемых заданий в общей системе проверяемых заданий;
3. взаимосвязь содержания и формы;
4. содержательная правильность заданий;
5. соответствие содержания работы уровню современного состояния науки;
6. системность содержания;
7. вариативность содержания;
8. возрастающая трудность заданий.
Форма и содержание являются главными компонентами процесса создания тестовых заданий.
Требования к заданиям:
1. цель;
2. краткость;
3. технологичность;
4. логическая форма высказывания;
5. одинаковость правил оценки ответов;
7. правильность расположения элементов задания;
8. одинаковость инструкции для всех испытуемых;
9. адекватность инструкции форме и содержанию задания.
Данные работы могут быть использованы на уроках повторения и систематизации материала после изучения каждого раздела и темы программы для выявления пробелов в знаниях учеников и их коррекции. Задания и вопросы в работах самые разнообразные. Одни из них позволяют выяснить усвоение учащимися терминов, определений, правил и связанного с ними теоретического материала, другие требуют демонстрации практических навыков.
Тексты заданий каждой темы состоят из шести пунктов, отличающихся как тематикой, так и сложностью. Это делает возможным их применение при дифференцированном подходе к каждому ученику.
По каждой работе приведены коды правильных ответов.
Тема: «Решение уравнений»
1 вариант
Решить уравнения
1) 3 – 4х = -5
2) 2,5 (х – 4) + 2 = 0,5
3) ( -6х + 1) : 4 = 2х : 3
4) 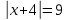
5) 4b – ax + 12 = 0
6) – 12х + 4 (х – 3) = - 8х -12
|
2 вариант
Решить уравнения
1) 35 (х + 1) = - 14
2) – 12 (2 - х) = - 6х + 2
3) (х + 3): 4 = (2х - 1 ) : 3
4) 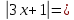 4 4
5) a (b – 3x) + 2 = 23
6) 12 (x + 2) – 2,1 = 2 (6x + 12) – 3x
|
3 вариант
Решить уравнения
1) 32x + (2 – 3x) = 5
2) – 4x + 21 + (3 - x) = 12
3) x : 4 = 2x : 3
4) 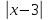 = 12 = 12
5) 3b – a (x - 3 ) = 2
6) – 2 (x + 21) – 3 (x - 14) = - 5x
|
4 вариант
Решить уравнения
1) 3x + 12 + x = - 4
2) – (3 - x) + 2 (x - 3) = 3
3) (x – 3,4) : 3 = (2x - 3 ) : 2
4) 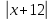 = 1 = 1
5) (x - a) : b = 12
6) – 11 (x - 2) + (2x - 3 ) = - 9x + 19
|
5 вариант
Решить уравнения
1) 12 – (x - 2) = 3
2) – (2x - 1) – 2 (5 – 3x) = 0
3) – (x - 2) : 5 = 2x : 3
4) 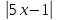 = 2 = 2
5) ax – 4bx + 12 = 9
6) – 11 (x - 2) + 2 (3 – 2x) + 15x = 0
|
6 вариант
Решить уравнения
1) 3 : (2x - 1 ) = 3
2) 2 (3 - x) – 21 (x - 1) =0
3) (2 – 3x) : 2 = (3 – 2x ) : 3
4) 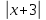 =12 =12
5) b – 2ax + 4 = 0
6) 2,1 (2 - x) + 1,4 (1,5x - 3) = 2
|
7 вариант
Решить уравнения
1) 3 (5x + 2) = 12
2) -7 (2 - x) + 2 ( x -3 ) = 0
3) (x - 2) : 5 = x : 3
4) 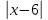 = 3 = 3
5) bx – 4a = 8
6) 21 (x -3) + 20 = 7 (3x - 2)
|
8 вариант
Решить уравнения
1) 21 (3 - x) = 12
2) 3x – 2 (2 - x) = 7 (x - 2)
3) 12 : (1 - x ) = 4 : (3x - 1 )
4) 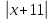 = 1 = 1
5) 2b – 2 (a + 3x) = 2b
6) 8 (2x - 1) – 2 (8x - 3 ) = 2
|
Ответы
№ задания
вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
2
|
4
|
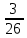
|
5; -13
|
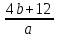
|
Бесконечное
множество
решений
|
2
|
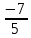
|
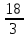
|
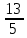
|
1;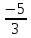
|
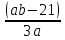
|
Нет
решений
|
3
|
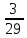
|
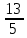
|
0
|
15; -9
|
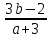
|
Нет
решений
|
4
|
- 4
|
4
|
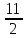
|
- 11; - 13
|
12b + a
|
Бесконечное
множество
решений
|
5
|
11
|
2
|
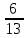
|
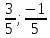
|
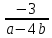
|
Нет
решений
|
6
|
1
|
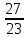
|
0
|
9; - 15
|
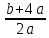
|
Нет
решений
|
7
|
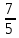
|
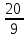
|
-3
|
9; 3
|
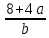
|
Нет
решений
|
8
|
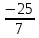
|
5
|
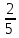
|
-10; -12
|
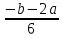
|
Нет
решений
|
Тема: «Преобразование выражений»
1 вариант
Упростить выражение
1) a – 5p – 5a + 3p
2) – (2a - p) – 3 (a + 2p)
3) 4y – 3 – 2 (5 - y)
4) 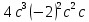
5) 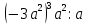
6) 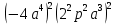
|
2 вариант
Упростить выражение
1) 3k – 4y + 2k – (-y)
2) 7 (1 - p) – 7 (2p - 1)
3) – (-3y – a) + (- a +2y)
4) 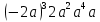
5) 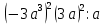
6) 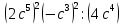
|
3 вариант
Упростить выражение
1) 4h – 8f + 2f – 12h
2) 3h – (-2 + h) – 12
3) – (-45k + 1) – 2 (30k + 5)
4) 3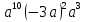
5) 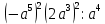
6) 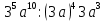
|
4 вариант
Упростить выражение
1) 21e – 11p + e –p
2) – (-p) + 4k – 2(p -2k)
3) 21 ( -2y – x) -3 (2x – 14y)
4) 5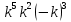
5) 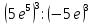
6) 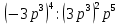
|
5 вариант
Упростить выражение
1) 2y – 6a – 12y + 12a
2) –(2 – a) – a + (2a + 1)
3) -21(-y – 2k) + 2(-y + 3k)
4) 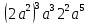
5) 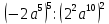
6) 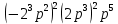
|
6 вариант
Упростить выражение
1) k – e – 2k – 2e +3k
2) -2(a – 4) + 10(-3a – 1)
3) 32(3k – y) – 21(5k +2y)
4) 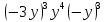
5) 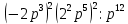
6) 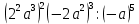
|
7 вариант
Упростить выражение
1) -23 – 2y + 13 + 3y
2) – (2 – y) + 3(3 – y)
3) -12(k – 2y) + 2(6k -10y)
4) 2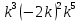
5) 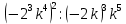
6) 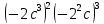
|
8 вариант
Упростить выражение
1) -2y -4k – 3a + 4y +3a
2) -3(1 – 3y) + 2(2y – 1)
3) 2(2y – 3k + 1) – (2 – 4y +5k)
4) 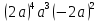
5) 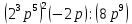
6) 12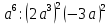
|
Ответы
№ задания
вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
-4a – 2p
|
-5a-5p
|
6y-22
|
16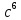
|
-27a
|
256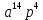
|
2
|
5k-3y
|
14-21p
|
5y
|
-16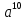
|
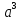
|
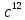
|
3
|
-8h-6f
|
2h-10
|
15k-11
|
27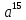
|
4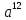
|
9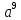
|
4
|
22e-12p
|
-p+8k
|
-27x
|
-5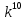
|
-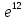
|
9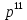
|
5
|
6a-10y
|
-1+2a
|
19y+48k
|
32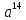
|
-2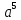
|
256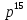
|
6
|
2k-3e
|
-32a-2
|
-9k-74y
|
27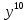
|
16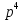
|
-2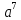
|
7
|
y-10
|
7-y
|
4y
|
8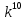
|
-8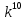
|
-256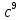
|
8
|
2y-4k
|
13y-1
|
8y-11k
|
64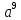
|
-16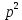
|
27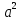
|
Тема: «Многочлены»
1 вариант
1) Упростить выражение
а) 5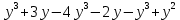
б) t(r – 4t) + 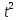 (4 + r) (4 + r)
2) Решить уравнение
а) 6x(x +2) – 0,5(12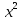 -7x)=31 -7x)=31
б) 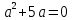
3) Разложить на множители
а) 16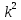 - 25 - 25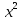
б) 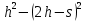
|
2 вариант
1) Упростить выражение
а) 2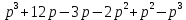
б) 3s (4s + 2) – 12(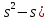
2) Решить уравнение
а) x (4x + 11) – 7(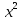 - 5x) = - 3 - 5x) = - 3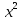 - 9x - 9x
б) 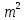 + 4m = 0 + 4m = 0
3) Разложить на множители
а) 16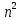 - 121 - 121
б) 9 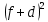 - 9 - 9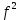
|
3 вариант
1) Упростить выражение
а) 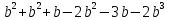
б) 3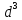 (d -2) + (d -2) + 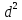 (4 -3 (4 -3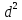 ) )
2) Решить уравнение
а) 16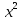 - (4x -1)(4x -3) =13 - (4x -1)(4x -3) =13
б) m(3m + 7) =0
3) Разложить на множители
а) 81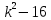
б) 16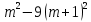
|
4 вариант
1) Упростить выражение
а) d + 2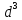 - 3 - 3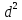 – 4d - 3 – 4d - 3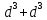
б) a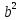 (b - (b - 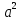 ) + ab( ) + ab(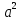 - - 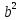 ) )
2) Решить уравнение
а) 15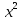 + (3x -2)(4 -5x) =14 + (3x -2)(4 -5x) =14
б) 4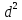 - 12d=0 - 12d=0
3) Разложить на множители
а) 1 - 4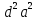
б) 81 - 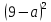
|
5 вариант
1) Упростить выражение
а) - 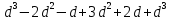
б) 8x (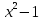 ) - 4 ) - 4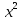 (2x + 1) (2x + 1)
2) Решить уравнение
а) 14x (x – 2) – ( 2x -1)(7x + 1) = -22
б) 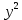 – 2(y – 1) = 2 – 2(y – 1) = 2
3) Разложить на множители
а) 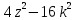
б) 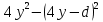
|
6 вариант
1) Упростить выражение
а) 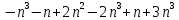
б) -2m (6m – 21) – 6m (7 – 2m)
2) Решить уравнение
а) (x - 4)(x + 3) –(x - 2)(x + 5) = 0
б) 5c(3c - 2) =0
3) Разложить на множители
а) 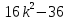
б) 16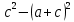
|
7 вариант
1) Упростить выражение
а) 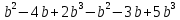
б) 6y(7y - 12) -7y(6y - 10)
2) Решить уравнение
а) (2x -1)(2x + 3) - 4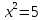
б) (2z - 1)(z + 7) =0
3) Разложить на множители
а) 49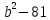
б) 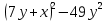
|
8 вариант
1) Упростить выражение
а) 8d + 4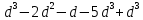
б) 9h(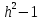 ) + 3 ) + 3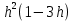
2) Решить уравнение
а) 49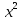 + (7x - 3)(2 – 7x) =29 + (7x - 3)(2 – 7x) =29
б) 14y - 49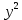 = 0 = 0
3) Разложить на множители
а) 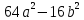
б) 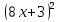 – 9 – 9
|
Ответы
№ задания
вариант
|
1
|
2
|
3
|
а
|
б
|
а
|
б
|
а
|
б
|
1
|
y(y+1)
|
tr(1+t)
|
2
|
0;-5
|
(4k-5x)(4k+5x)
|
(s-h)(3h-s)
|
2
|
p3-p2+9p
|
18s
|
0
|
0;-4
|
(4n-11)(4n+11)
|
3d(3d+6f)
|
3
|
-2b(b2+1)
|
2d2(-3d+2)
|
1
|
0;-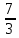
|
(9k-4)(9k+4)
|
(m-3)(7m+3)
|
4
|
-3d(d+1)
|
a3b(1-b)
|
1
|
0;3
|
(1-2da)(1+2da)
|
a(18-a)
|
5
|
d(d+1)
|
-4x(x+2)
|
1
|
0;2
|
(2z-4k)(2z+4k)
|
(-2y+d)(6y-d)
|
6
|
2n2
|
0
|
-0,5
|
0;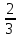
|
(4k-6)(4k+6)
|
(3c-a)(5c+a)
|
7
|
7b(b-1)(b+1)
|
-2y
|
2
|
0,5; -7
|
(7b-9)(7b+9)
|
x(14y+x)
|
8
|
d(-2d+7)
|
3h(h-3)
|
1
|
0;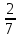
|
(8a-4b)(8a+4b)
|
8x(8x+6)
| |
|
|
 Скачать 39.02 Kb.
Скачать 39.02 Kb.
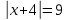
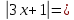 4
4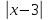 = 12
= 12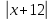 = 1
= 1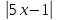 = 2
= 2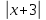 =12
=12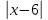 = 3
= 3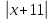 = 1
= 1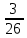
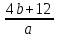
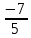
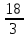
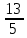
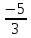
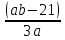
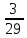
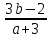
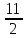
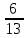
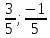
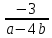
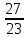
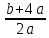
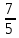
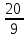
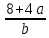
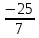
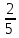
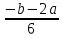
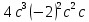
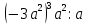
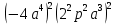
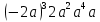
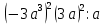
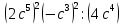
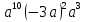
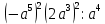
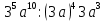
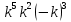
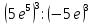
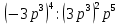
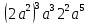
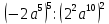
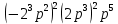
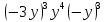
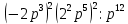
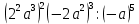
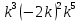
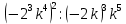
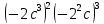
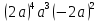
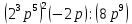
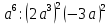
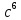
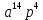
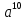
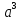
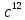
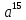
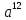
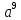
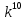
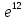
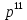
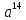
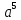
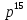
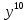
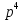
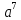
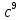
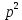
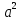
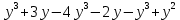
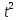 (4 + r)
(4 + r)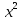 -7x)=31
-7x)=31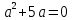
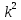 - 25
- 25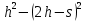
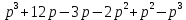
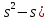
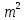 + 4m = 0
+ 4m = 0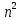 - 121
- 121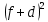 - 9
- 9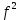
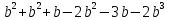
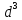 (d -2) +
(d -2) + 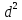 (4 -3
(4 -3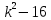
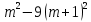
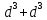
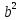 (b -
(b - 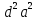
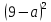
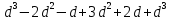
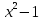 ) - 4
) - 4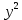 – 2(y – 1) = 2
– 2(y – 1) = 2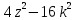
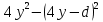
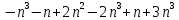
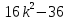
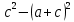
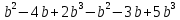
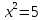
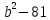
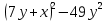
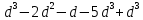
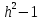 ) + 3
) + 3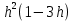
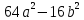
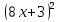 – 9
– 9