ргр. Решение Уравнения движения

• Название: Решение Уравнения движения
• Дата: 14.10.2022
• Размер: 168.67 Kb.
• Имя файла: ргр.docx
• Тип: Документы; #733715

Дано: уравнения движения точки M
𝑥 = 5𝑐𝑜𝑠( ^П𝑡2)

{ ³ (1)

𝑦 = −5𝑠𝑖𝑛(^П𝑡2)

3
Найти: Необходимо установить вид траектории движения точки M и для момента времени t=t1=1c, найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение: Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1).
Получаем 𝑥² + 𝑦² = 5² , т.е. траекторией точки является окружность (рисунок 1.1).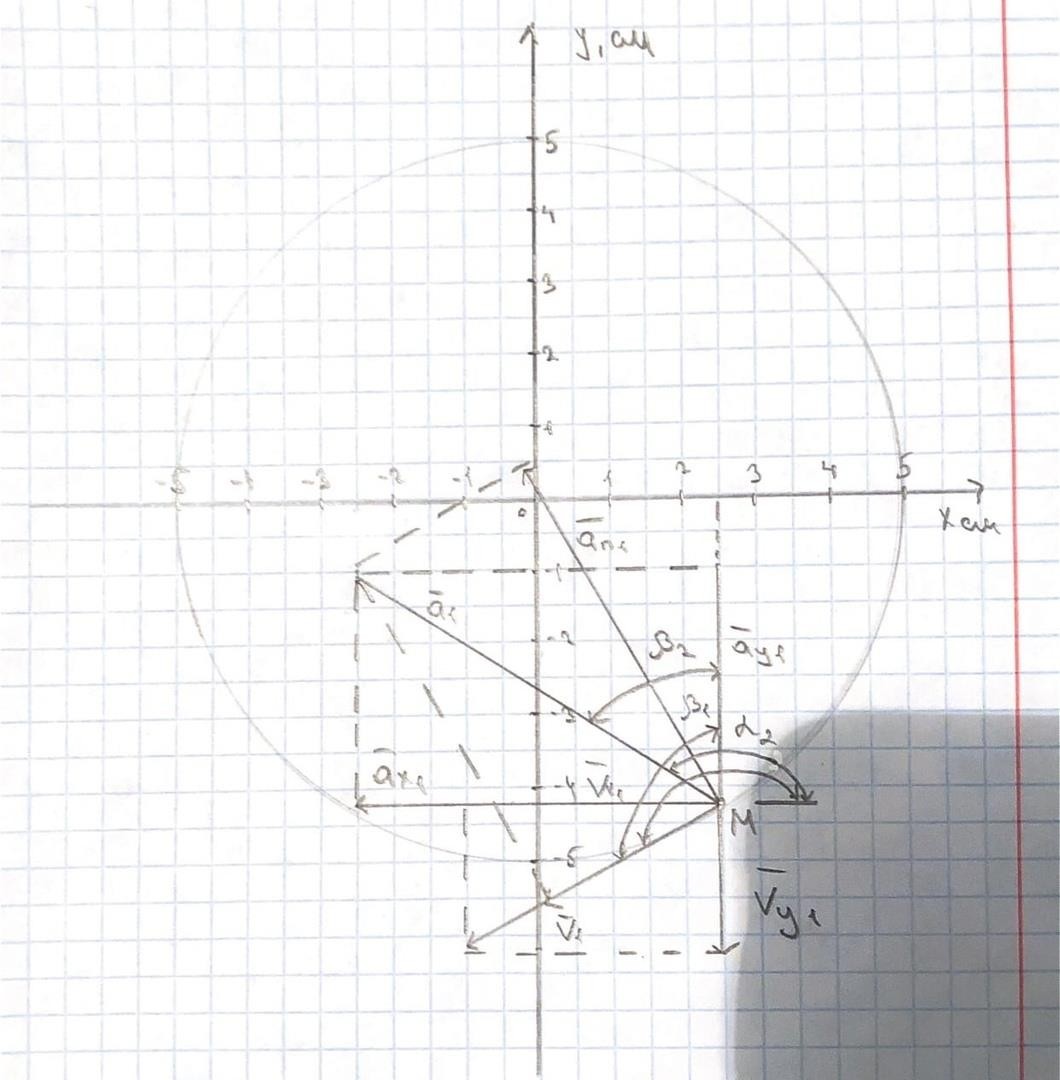



Вектор скорости точки

𝑣̅ = 𝑣_𝑥𝑖̅ + 𝑣_𝑦𝑗̅ (2)

Вектор ускорения
𝑎̅ = 𝑎_𝑥𝑖̅ + 𝑎_𝑦𝑗

Здесь i , j – орты осей x и y; 𝑣_𝑥, 𝑣_𝑦, 𝑎_𝑥, 𝑎_𝑦 – проекции скорости и ускорения точки на оси координат. Найдем их, дифференцируя по времени уравнения движения (1),

𝑣_𝑥 = 𝑥’ = −9,06;

𝑣_𝑦 = 𝑦’ = −5,23;

𝑎_𝑥 = 𝑥” = −20,02;

𝑎_𝑦 = 𝑦” = 13,74; (3)

По найденным проекциям определяются модуль скорости

^{𝑣 =} √^{𝑣2 + 𝑣2 = 10,47 (см/с2) (4)}

и модуль ускорения точки

𝑥 𝑦

^{𝑎 =} √^{𝑎2 + 𝑎2 = 24,28 (см/с2) (5)}

𝑥 𝑦

или

Модуль касательного ускорения точки


(6)
𝑑𝑣

𝑎_𝑐 = |_𝑑𝑡|

𝑎_𝑐

= |^{𝑣𝑥𝑎𝑥+𝑣𝑦𝑎𝑦}| = 10,47 (см/с²) (7)

𝑣

Здесь 𝑑𝑣/𝑑𝑡 выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 𝑑𝑣/𝑑𝑡 означает, что движение точки ^{ускоренное, направления 𝑎̅}𝛕 ^{и 𝑣̅ совпадают; знак «–» – что движение} замедленное.
Модуль нормального ускорения точки

𝑎<sub>𝑛

= 𝑣</sub>2

𝜌

(8)

Если радиус кривизны траектории  в рассматриваемой точке неизвестен, то 𝑎_𝑛 можно определить по формуле




𝑐
𝑎_𝑛=√𝑎² − 𝑎² (9)
При движении точки в плоскости формула (8) принимает вид

_{𝑎 =} |𝑣_𝑥𝑎_𝑦−𝑣_𝑦𝑎_𝑥| ₂

𝑛
=21,91(см/с

𝑣

) (10)

Модуль нормального ускорения можно определить и следующим образом:

𝑎_𝑛 = √𝑎² − 𝑎²=21,91 (см/с²) (11)

𝑐
После того как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения

𝜌 = ^𝑣2 =5(см) (12)

𝑎_𝑛
Результаты вычислений по формулам (3) – (5), (7), (11) и (12) для заданного момента времени t₁=1 c приведены в таблице 1.1.

Координаты , см		Скорость, см/с			Ускорение, см/с2						Радиус кривиз ны, см
x	y	𝑣𝑥	𝑣𝑦	𝑣		𝑎𝑥	𝑎𝑦	𝑎	𝑎𝑐	𝑎𝑛		ρ
2,5	-4,33	-	-	10,47		-	13,	24,	10,4	21,91		5
		9,0	5,23			20,	74	28	7
		6				02

Таблица 1.1