Решение уравнения 
|



|
Решение уравнения
b– четное число
|
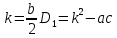

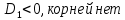
|
Разложение квадратного трехчлена на множители
|
 , где , где 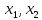 корни квадратного трехчлена корни квадратного трехчлена
|
Свойства степени с целым показателем для любого а и любых целых m и n.
|
am ∙ an = am+n am : an = am-n
(am)n = amn (ab)n = anbn

|
Перенос слагаемых в неравенствах.
|
Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
|
Арифметическим квадратным корнем из числа а
|
Называется неотрицательное число, квадрат которого равен а.
|
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен.
|
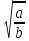 = = , a , a b b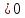 . .
|
Квадратный корень из степени с четным показателем.
|
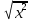 = = 
|
Решение уравнения с двумя переменными
|
Пара значений переменных, обращающая уравнение в верное равенство.
|
Разложение квадратного трехчлена на множители
|
Если 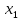 и и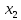 - корни квадратного трехчлена а - корни квадратного трехчлена а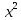 +bx +с, то а +bx +с, то а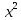 +bx+с = а(х- +bx+с = а(х-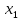 )(х- )(х-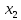 ) )
|
 Скачать 17.41 Kb.
Скачать 17.41 Kb.