Решение а б

• Название: Решение а б
• Дата: 13.12.2022
• Размер: 488.5 Kb.
• Имя файла: 722-р.doc
• Тип: Решение; #843751

Задание 1

Найти указанные пределы.

3) а) ;

б) ;

в) ;

г) ;

д) .

Решение.

а)





б)

при x=2 числитель и знаменатель дроби равны 0, имеем неопределённость вида . Преобразуем исходную дробь числитель и знаменатель разложив на множители:



в)

при x=0 числитель и знаменатель дроби равны 0, имеем неопределённость вида 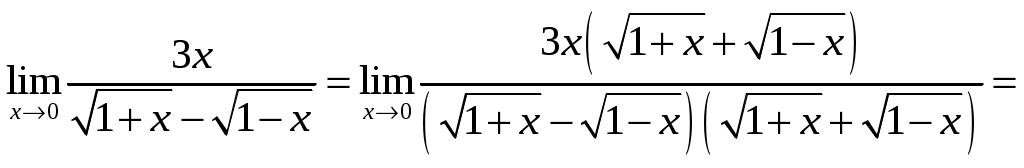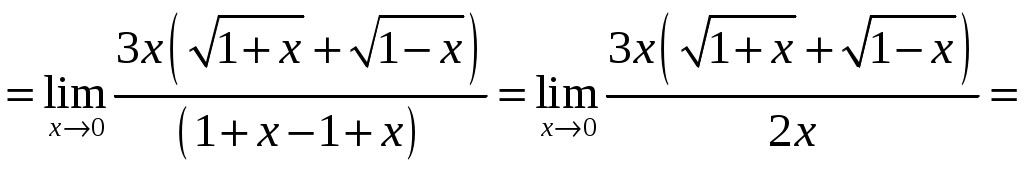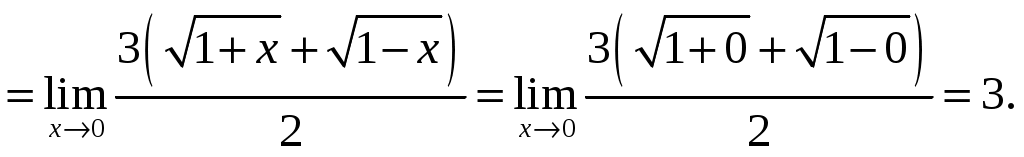. Преобразуем исходную дробь помножив числитель и знаменатель на сопряженное знаменателя и преобразовав числитель:







г)

при x= имеем неопределённость вида . Преобразуем исходное выражение и воспользуемся первым замечательным пределом :



д)


Задание 2

Найти производные .

3. 
   а) ;
   

б) ;

в) ;

г) ;

д) .

Решение.

а) .



.

б) .



в) .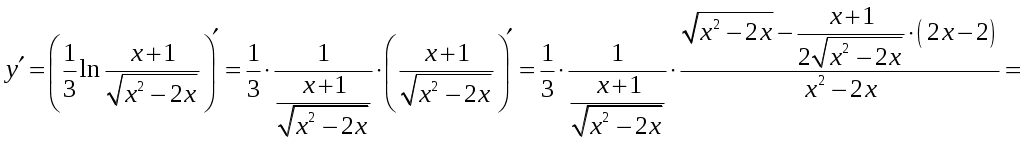

.

г) .





д) .

Дифференцируем обе части равенства:

;

;

;




Задание 3

Найти наибольшее и наименьшее значения функций у=f(х) на отрезке [a,b].

3. 
   ,[-5,5].
   

Решение.

Находим значения функции на концах заданного отрезка:

.

Находим производную заданной функции: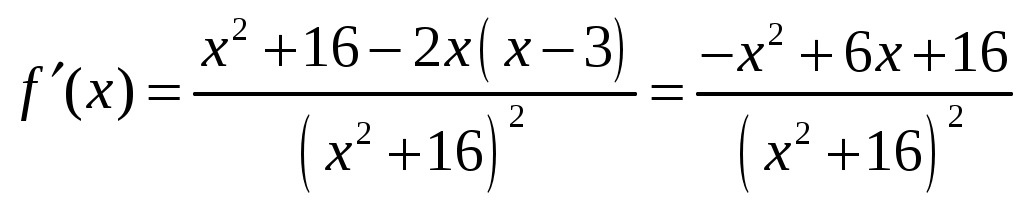

.

Приравняем производную к нулю и найдем критические точки: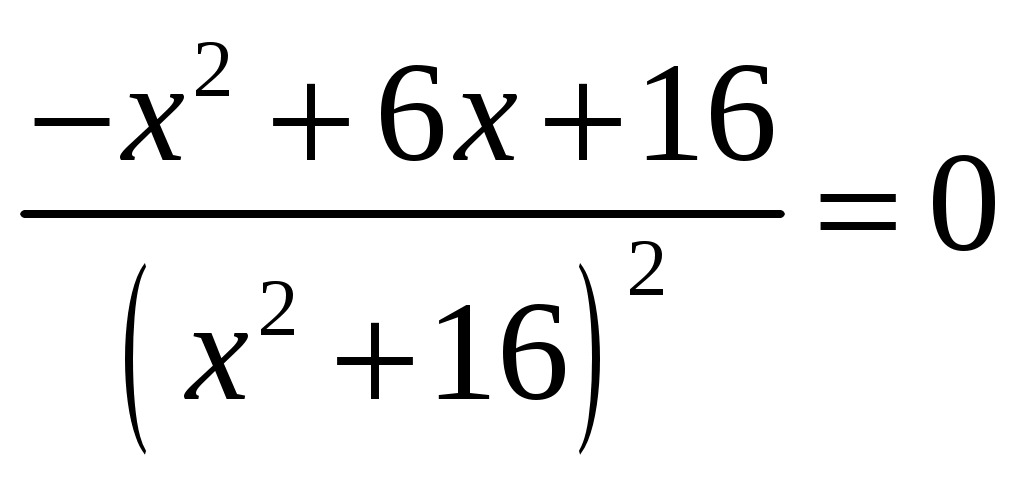

,

Точка . Значит критическая точка .

Исследуем характер данной точки:




- +



-2

Данная точка– точка экстремума минимума.

Находим значение функции в данной точке:



Получаем:

Задание 4

Город В стоит на железной дороге, идущей с юга на север. Рудник А расположен южнее города В на b км и отстоит от железной дороги на a км. В какую точку Р железной дороги следует построить подъездной путь от рудника, чтобы транспортировка грузов из А в В была наиболее экономичной, если стоимость провоза 1 т груза на расстоянии 1 км по подъездному пути обходится в k раз дороже, чем по железной дороге (рис.1).



b В




Ю Д С




Р

а
А

Рис.1


Решение.

Пусть расстояние от точки Д до точки Р равно , тогда подъездной путь (AP) по теореме Пифагора:

.

Путь по железной дороге будет: .

Тогда общие затраты на транспортировку груза из точи А в точку В будут равны: .

Находим производную данной функции: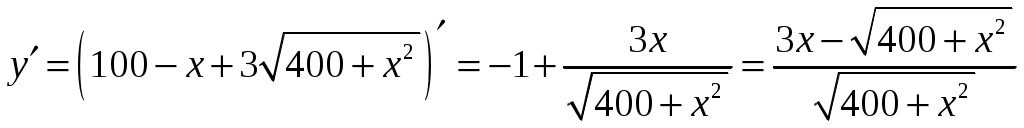

.

Приравняем производную к нулю и находим критические точки: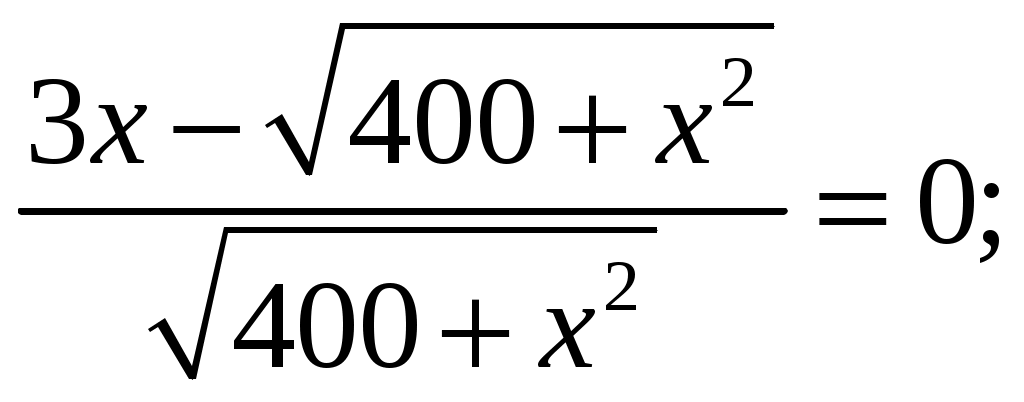



.

По смыслу задачи расстояние не может быть отрицательным, тогда .

Исследуем характер данной точки:




- +





Данная точка– точка экстремума минимума.

Получаем, что для наиболее экономичной транспортировки грузов из А в В необходимо построить подъездной путь в точку Р железной дороги на расстоянии от точки В.

Задание 5

Исследовать методами дифференциального исчисления и построить графики функций.

3. 
   .
   

Решение.

Для полного исследования функции и построения ее графика применяется следующая примерная схема:

1. 
   найти область определения функции;
   
2. 
   исследовать функцию на непрерывность и определить характер точек разрыва;
   
3. 
   исследовать функцию на четность и нечетность, периодичность;
   
4. 
   найти точки пересечения графика функции с осями координат;
   
5. 
   исследовать функцию на монотонность и экстремум;
   
6. 
   найти интервалы выпуклости и вогнутости, точки перегиба;
   
7. 
   найти асимптоты графика функции;
   
8. 
   по полученным данным построить график функции.
   

Применим вышеуказанную схему для исследования данной функции.

1. 
   .
   
2. 
   Функция не определена в точке . Следовательно, есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:
   

Следовательно, – точка разрыва второго рода;

3. 
   .
   

Функция не является ни четной, ни нечетной. Функция не периодическая.

4. 
   С осью Ох: .
   

Точка – точка пересечения с осью Ох.

С осью Оу: .

Точка – точка пересечения с осью Оy.

5. 
   Находим производную.
   

при и не существует при .

Критическая точка: .



- + -




-1 1
Функция убывает на интервалах ; возрастает – на интервале .

6. 
   Находим вторую производную.
   

при и не существует при .

Критическая точка второго рода: .



- +



-2
Функция вогнута на интервалах , функция выпукла на интервале .

Точка перегиба , .

7. 
   Так как точка - точка разрыва второго рода, то прямая - вертикальная асимптота.
   

Найдем наклонные асимптоты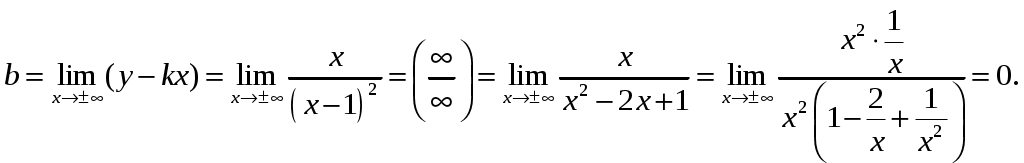





Тогда - горизонтальная асимптота

8. 
   По полученным данным строим график функции.
   

Задание 6

Вычислить неопределенный интеграл

3. 
   а) , результат проверить дифференцированием
   

б) ; в) ;г) ; д) ; е) .

Решение.

а) .



Проверка: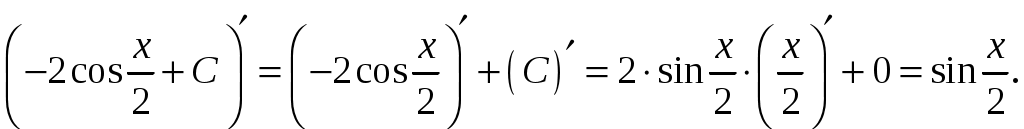



Ответ: =

б) .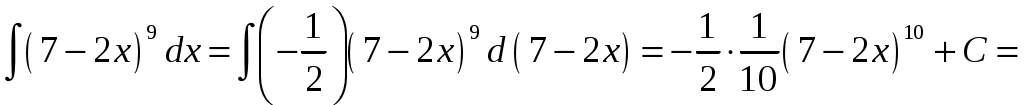





в) .



г)



д) .



е)

Применим подстановку: , тогда , , получаем:





Задание 7

Вычислить неопределенный интеграл, применяя метод интегрирования «по частям».

3. 
   а) ,
   

б)

Решение.

а) .

Применим формулу интегрирования по частям .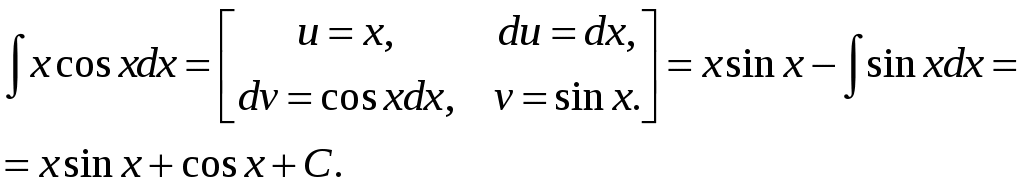



б) .

Применим формулу интегрирования по частям .



Ответ: а) б) .