Сопромат. Устойчивость.. ПЗ от 04.05. Решение. Условие устойчивости решается при подборе сечения методом последовательных приближений
 Скачать 189.98 Kb. Скачать 189.98 Kb.
|
|
Подбор сечения сжатых стержней Пример 1. Подобрать сечение сжатой стойки, изображенной на рис. 1, если F = 300 кН, l = 3 м, 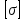 = 100 МПа, Е = 100 ГПа. Также определить значение критической силы и коэффициента запаса устойчивости. = 100 МПа, Е = 100 ГПа. Также определить значение критической силы и коэффициента запаса устойчивости. Рис. 1 Решение. Условие устойчивости 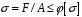 решается при подборе сечения методом последовательных приближений. решается при подборе сечения методом последовательных приближений.Шаг 1. Так как 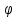 может изменяться от 0 до 1, то зададимся первым значением может изменяться от 0 до 1, то зададимся первым значением 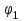 = 0,5. Тогда = 0,5. Тогда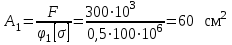 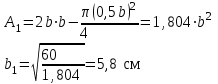 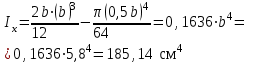 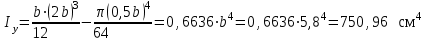 Наименьшим будет Iх 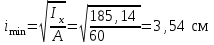 Определим гибкость стержня: 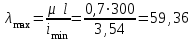 . .Используем Приложение 4 (см. доп. материалы к занятию): 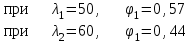 С учетом значения λmax = 59,36 имеем 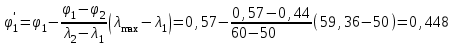 . .Допускаемое напряжение на устойчивость составляет 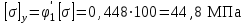 Действующее напряжение 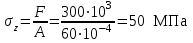 Перенапряжение составляет 11,6 %, что больше допускаемых 5%, следовательно, сечение нужно увеличить. Шаг 2. Примем 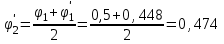 . . Тогда 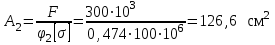 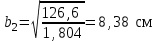 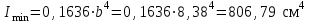 Радиус инерции 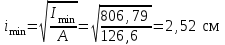 Определим гибкость стержня: 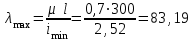 . .Используем Приложение 4 (см. доп. материалы к занятию): 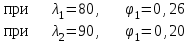 С учетом значения λmax = 83,19 имеем 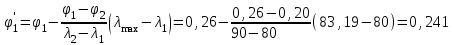 . .Допускаемое напряжение на устойчивость составляет 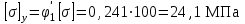 Действующее напряжение 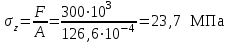 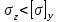 Принимаем сечение, для которого A = 126,6 см2, Iх = 806,79 см4, iх = 2,52 см. 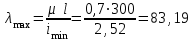 Для чугуна 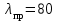 , , 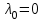 . .Так как 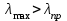 , то заданный стержень является стержнем большой гибкости и критическая сила определяется по формуле Эйлера: , то заданный стержень является стержнем большой гибкости и критическая сила определяется по формуле Эйлера: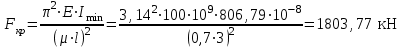 Коэффициент запаса устойчивости 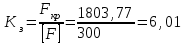 Пример 2. Подобрать сечение сжатой стойки, изображенной на рис. 2, если F = 400 кН, l = 4 м, 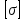 = 160 МПа, Е = 200 ГПа. Также определить значение критической силы и коэффициента запаса устойчивости. = 160 МПа, Е = 200 ГПа. Также определить значение критической силы и коэффициента запаса устойчивости.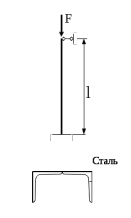 Рис. 2 Решение. Условие устойчивости 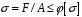 решается при подборе сечения методом последовательных приближений. решается при подборе сечения методом последовательных приближений.Шаг 1. Так как 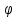 может изменяться от 0 до 1, то зададимся первым значением может изменяться от 0 до 1, то зададимся первым значением 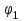 = 0,5. Тогда = 0,5. Тогда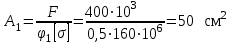 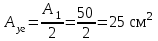 Из ГОСТ 8509-86 подбираем сечение по ближайшему наибольшему значению - уголок 100х100х14: А = 26,28 см2, 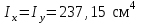 , , 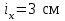 , , 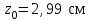 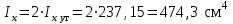 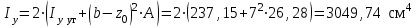 Наименьшим будет Iх 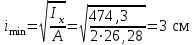 Определим гибкость стержня: 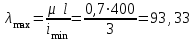 . .Используем Приложение 4 (см. доп. материалы к занятию): 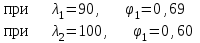 С учетом значения λmax = 93,33 имеем 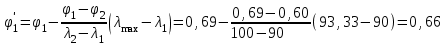 . .Допускаемое напряжение на устойчивость составляет 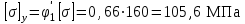 Действующее напряжение 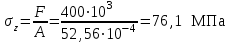 Недонапряжение составляет 39 %, что больше допускаемых 5%, следовательно, сечение нужно уменьшить. Шаг 2. Примем 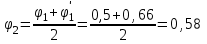 . . Тогда 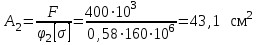 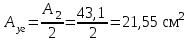 Из ГОСТ 8509-86 подбираем сечение по ближайшему наибольшему значению - уголок 100х100х12: А = 22,8 см2, 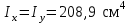 , , 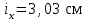 , , 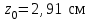 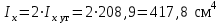 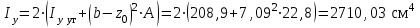 Наименьшим будет Iх 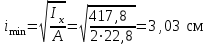 Определим гибкость стержня: 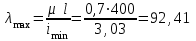 . .Используем Приложение 4 (см. доп. материалы к занятию): 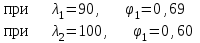 С учетом значения λmax = 92,41 имеем 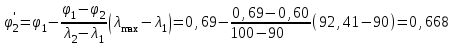 . .Допускаемое напряжение на устойчивость составляет 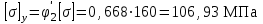 Действующее напряжение 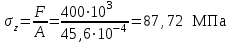 Недонапряжение составляет 22 %, что больше допускаемых 5%, следовательно, сечение нужно еще уменьшить. Шаг 3. Примем 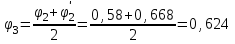 . . Тогда 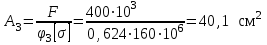 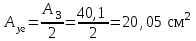 Из ГОСТ 8509-86 подбираем сечение по ближайшему наибольшему значению. По расчету получаем тот же самый уголок, что и в шаге 2, но нужно взять меньше сечение, так как было недонапряжение. Поэтому принимаем уголок 100х100х10: А = 19,24 см2, 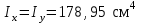 , , 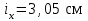 , , 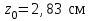 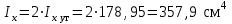 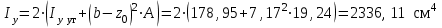 Наименьшим будет Iх 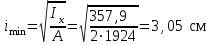 Определим гибкость стержня: 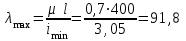 . .Используем Приложение 4 (см. доп. материалы к занятию): 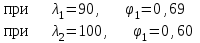 С учетом значения λmax = 91,8 имеем 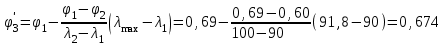 . .Допускаемое напряжение на устойчивость составляет 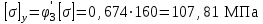 Действующее напряжение 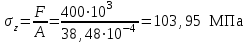 Недонапряжение составляет 3,5 %, что меньше допускаемых 5%, 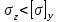 Принимаем сечение в виде двух уголок, для которого A = 38,48 см2, Iх = 357,9 см4, iх = 3,05 см. 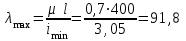 Для стали 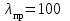 , , 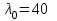 . .Так как 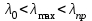 , то заданный стержень является стержнем средней гибкости и критическая сила определяется по формуле Ясинского: , то заданный стержень является стержнем средней гибкости и критическая сила определяется по формуле Ясинского: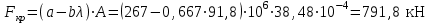 Коэффициент запаса устойчивости 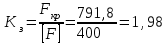 |
