Решение. Условие задачи можно записать как вероятность того, что погрешность измерения не превысит 20 мА, равна 0 р
 Скачать 36.07 Kb. Скачать 36.07 Kb.
|
|
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ ПРЯМЫХ ИЗМЕРЕНИЙ 3. 1 В результате поверки амперметра установлено, что 80% погрешностей результатов измерений, произведенных с его помощью, не превосходит 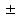 20 мА. Считая, что погрешности подчиняются нормальному закону с нулевым математическим ожиданием, найти вероятность того, что погрешность результата измерения превзойдет 20 мА. Считая, что погрешности подчиняются нормальному закону с нулевым математическим ожиданием, найти вероятность того, что погрешность результата измерения превзойдет 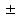 40 мА. 40 мА.Решение. Условие задачи можно записать как вероятность того, что погрешность измерения Δ не превысит ±20 мА, равна 0,8. Р(|Δ|< 20 мА)=0,8. Значение этой вероятности равно нормированному интегралу Лапласа 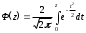 при z= при z=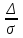 . .По таблице приложения А находим для Ф(z)=0,8 значение аргумента z=1,28. Следовательно, среднеквадратическая погрешность измерений этим амперметром равна σ =Δ/z= 20/1,28=15,6 мА. Вероятность того, погрешность измерения не превысит 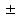 40 мА, равна Р(|Δ|< 40 мА)=Ф(z)=Ф( 40 мА, равна Р(|Δ|< 40 мА)=Ф(z)=Ф(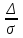 )=Ф(40/15,6)=Ф(2,55). )=Ф(40/15,6)=Ф(2,55).По таблице /1/ находим для z=2,55 значение Ф(2,55)=0,989. Вероятность того, что погрешность результата измерения будет больше 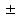 40 мА равна 40 мА равна 1-0,989=0,011. Ответ: 1,1%. 3.2 Завод изготавливает детали. Номинальный размер детали R0=5 см. Вследствие неточности изготовления фактический размер деталей – случайная величина, распределенная по нормальному закону со средним значением R0 и среднеквадратическим отклонением 0,05 см. При контроле бракуются все детали, размер которых отличается от номинального больше чем на 0,1 см. Определить, какой процент деталей будет отбраковываться? Решение. По условию σ=0,05 см, Δ=0,1 см. Задача решается с использованием нормированного интеграла Лапласа 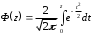 при z= при z=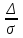 . .Вероятность того, что фактический размер детали будет отличаться от номинала не более чем на 0,1 см, равна Р(|Δ|< 0,1 см)=Ф(z)=Ф( 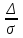 )=Ф(0,1/0,05)=Ф(2). )=Ф(0,1/0,05)=Ф(2).По таблице нормированного интеграла /1/ для аргумента z=2 находим значение самой функции Ф= 0,955. Это значит, что при данной точности изготовления, процент годных деталей равен 95,5%, а 4,5% деталей будут отбраковываться. Ответ: 4,5% брака. 3.3 Случайная погрешность измерения сопротивления распределена по нормальному закону. Оценка СКП 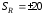 Ом. Определить границы симметричного доверительного интервала, за которые с вероятностью Ом. Определить границы симметричного доверительного интервала, за которые с вероятностью 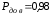 не выйдет случайная погрешность отдельного результата измерений. не выйдет случайная погрешность отдельного результата измерений.Решение. Границы симметричного доверительного интервала определяется формулой. 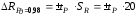 (Ом). (Ом).Для 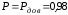 значение безразмерного коэффициента значение безразмерного коэффициента 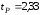 . .Следовательно, 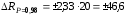 (Ом). (Ом).Ответ: С доверительной вероятностью 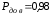 погрешность отдельного результата измерения не выйдет за границы погрешность отдельного результата измерения не выйдет за границы 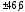 Ом. Ом. |
