идентификация. ответы. Решение. В данном случае N100 t4000 час t 100 час n(t)20 n(t)50

• Название: Решение. В данном случае N100 t4000 час t 100 час n(t)20 n(t)50
• Анкор: идентификация
• Дата: 07.06.2021
• Размер: 167.6 Kb.
• Имя файла: ответы.docx
• Тип: Решение; #215177

54. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. За интервал времени 4000 - 4100 час. отказало ещё 20 изделий. Требуется определить f*(t),   λ*(t) при t=4000 час. 
Решение. В данном случае N=100; t=4000 час; Δt =100 час; Δn(t)=20; n(t)=50.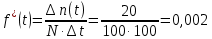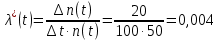

 





55. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. Требуется определить p*(t) и q*(t) при t=4000 час.

 В данном случае N= 100; n(t)=100-50=50; N-n(t)=100-50=50. По формулам определяем: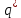


(t)=

(t)=


Р(4000)= 50/100=0,5

q(4000)=50/100=0,5

56. В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час. отказал еще один гироскоп. Требуется определить f*(t), λ*(t) при t =1000 час.

 В данном случае N=10; t=1000 час; Δt =100 час; Δn(t)=1; n(t)=8.




f*(1000) = 1/ 10*100 = 1*10^-2 1/час
λ*(1000) = 1/ 100*8 = 1,25*10 1/час

57. На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час. отказало 80 ламп. За интервал времени 3000 - 4000 час. отказало еще 50 ламп. Требуется определить p*(t) и q*(t) при t=4000 час.

В данном случае N= 1000; n(t)=1000-80-50=870; N-n(t)=1000-870=130. По формулам определяем: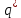


(t)=

(t)=
q*(t) = 1000-870/1000=1,3*10^-2 1/час
p*(t) = 870/1000=8,7*10^-2 1/час

58. На испытание поставлено 1000 изделий. За время t=1300 час. вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час. вышло из строя еще 13 изделий. Необходимо вычислить p*(t) при t=1300час.

и t=1400 час.; f*(t), λ *(t) при t =1300 час.
Решение. В данном случае N=1000; t=1300 час; Δt =100 час; Δn(t)=13; n(t)=288; n(1300)=1000-288=712; n(1400)=1000-288-13=699

 





(t)=

(1300)=

(1400)=

59. На испытание поставлено 45 изделий. За время t=60 час. вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час. вышло из строя еще 3 изделия. Необходимо вычислить p*(t) при t=60час. и t=65 час.; f*(t), λ *(t) при t =60 час.

Решение. В данном случае N=45; t=60 час; Δt =5 час; Δn(t)=3; n(t)=35; n(60)=45-35=10; n(65)=45-35-3=7

 





(t)=

(60)=

(1400)=

60. В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в таблицу. Необходимо определить m_t*.

Таблица

ti,час.	ni	ti,час.	ni	ti,час.	ni
0-10	19	30-40	3	60-70	1
10-20	13	40-50	0
20-30	8	50-60	1

61. На испытание поставлено 8 однотипных изделий. Получены следующие значения t_i (t_i - время безотказной работы i-го изделия):

t₁ =560час.; t₂=700час.; t₃ =800час.; t₄=650час.; t₅=580час.; t₆=760час.; t₇=920час.; t₈=850час.

Определить статистическую оценку среднего времени безотказной работы изделия.

Стат оценка ср вр-ни безотк работы

62. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t₁ =15мин.; t₂=20мин.; t₃ =10мин.; t₄=28мин.; t₅=22мин.; t₆=30мин.

Требуется определить среднее время восстановления аппаратуры.
Среднее время восстан-ния аппаратуры

63. На испытание поставлено 1000 изделий. За время t=11000 час. вышло из строя 410 изделий. Зв последующий интервал времени 11000-12000 час. вышло из строя еще 40 изделий. Необходимо вычислить p*(t) при t=11000 час. и t=12000 час., а также f*(t), λ *(t) при t=11000 час.
N=1000, T=11000час, Δt=1000час, n(t)=(1000-410)=590, Δn(t)=40.

Решение:

P^*(11000)=n(t)/N = 590/1000=0,59

P^*(12000)=n(t)/N = 40/1000=0,04

f^*(11000)=Δn(t)/N*Δt=40/1000*1000=0,04*10^-3 1/час

λ^*(е)= Δn(t)/Δt*n(t)=40/1000*590=0,07*10^-3 1/час

64. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы.
P=0,9, t=120 час.
Решение:

P(t) = e^-λ*t

P(120)= e^-λ*120

λ=8,8*10^-4 1/час

f(t)=λ(t)*P(t)

f(t)=8,8*10^-4*0,9=7,92*10^-4

m_(t)=1/λ=1/8,8*10^-4=1136 час.

65. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов.
m(t)=640 час, t=120 час.

Решение:

m_(t)=1/λ

λ=1/640=1,56 *^10-3 1/час.

P(t) = e^-λ*t

P(120)= e^{—1,56*10-3*120}=0,42

f(120)=λ(120)*P(120)

f(120)=1,56*10^-3*0,42=0,65*10^-3 1/час

66. Время работы изделия подчинено нормальному закону с параметрами m_t = 8000 час., σ_t =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , λ(t) для t=8000 час.



67. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами α=2,6 ; λ= 1,65*10^-7 1/час.

Требуется вычислить количественные характеристики надежности Р(t), f(t), λ(t) для t=150 час. и среднее время безотказной работы шарикоподшипников.


68. Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено экспоненциальному закону. Требуется определить количественные характеристики надежности f(t), λ (t), m_t.



69. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено экспоненциальному закону. Необходимо найти его количественные характеристики надежности P(t), f(t), λ (t) для t=1000 час.

Дано:

T=1260ч

t=1000ч

p(t)-?

λ(t)-?

f(t)-?

Решение:

1) -интенсивность отказа

2)Варианты безотказной работы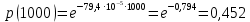





3) Частота отказов





70. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e^-t (1-e^-t) . Необходимо найти количественные характеристики надежности P(t), λ (t), m_t.

Дано:

f(t)=2e^-t (1-e^-t)

p(t)-?

λ(t)-?

m_t-?
Решение:

1)

=1-2 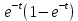– вероятность безотказной работы на интенсивность времени от 0 до t

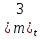2) интенсивность отказов изделия

= среднее время безотказной работы изделия

71. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e^-t-3e^-2t+e^-3t.

Требуется найти количественные характеристики надежности P(t), λ (t), m_t.

Дано:

f(t)=

p(t)-?

λ(t)-?

m_t-?
Решение:

1)

2)



3)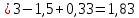



72. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы m_t=1500 час. и среднее квадратическое отклонение σ_t = 100 час.

Дано: t=1300 ; m_t=1500 час; ; P-?; λ-?

Решение: по эксп. закону ; ;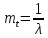

По нормальному закону: ; ;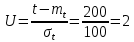

; ; f(t)= 0,54*10^-4 1/час;

λ(t) = f(t)/P(t) = 0,0024 1/час

73. Аппаратура связи состоит из 2000 элементов, средняя интенсивность отказов которых λ ср= 0,33 * 10^-5 1/час.

Необходимо определить вероятность безотказной работы аппаратуры в течении t = 200 час и среднее время безотказной работы аппаратуры.

Дано: n=2000 эл; λ ср= 0,33 * 10^-5 1/час; P(200) -?; m_t=?

Решение: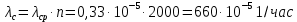





74. Невосстанавливаемая в процессе работы электронная машина состоит из 200000 элементов, средняя интенсивность отказов которых λ =0,2 * 10^-6 1/час. Требуется определить вероятность безотказной работы электронной машины в течении t = 24 часа и среднее время безотказной работы электронной машины.

Дано: n=200000 эл; λ ср= 0,2 * 10^-6 1/час; P(24) -?; m_t=?

Решение:





75. Система управления состоит из 6000 элементов, средняя интенсивность отказов которых λ ср. = 0,16*10^-6 1/час. Необходимо определить вероятность безотказной работы в течении t = 50 час и среднее время безотказной работы.
Дано:

n= 6000

λ_ср=0.16*10^-6 1/час

p(50)-?

m_t-?
Решение:

1) λ_с = λ_ср * n = 0.16*10^-6 *6000 = 960*10^-6 1/час

2)

3)

76. Прибор состоит из n = 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P₁(t)=0,98; P₂(t)=0,99; P₃(t)=0,998; P₄(t)=0,975; P₅(t)=0,985. Необходимо определить вероятность безотказной работы прибора.
Дано:

n = 5

P₁(t)=0,98

P₂(t)=0,99

P₃(t)=0,998

P₄(t)=0,975

P₅(t)=0,985
P_с(t)= ?

Решение:

При последовательном соединении: P_с(t)=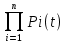

P_с(t)= P₁(t)*P₂(t)*P₃(t)*P₄(t)*P₅(t)

P_с(t)= 0,98*0,99*0,998*0,975*0,985=0.9299

77. Система состоит из пяти приборов, среднее время безотказной работы которых равно: m_t1=83 час; m_t2=220 час; m_t3=280 час; m_t4=400 час; m_t5=700 час. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы системы.

Дано:

n=5

m_t1=83 час

m_t2=220 час

m_t3=280 час

m_t4=400 час

m_t5=700 час
m_ср=?
Решение:
Экспоненциальный закон надежности: m_ср=1/λ

Среднее время безотказной работы системы:

m_cр =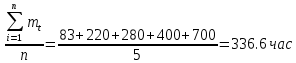

78. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t=50 час равна: P₁(50)=0,98; Р₂(50)=0,99; Р₃(50)=0,998; Р₄(50)=0,975; Р₅(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.

Решение:

Найдем вероятность безотказной работы системы Р_с(t)= p_i(t)

P_c(50)=0,98*0,99*0,998*0,975*0,985=0,929

Исходя из экспоненциального закона, найдем интенсивность отказов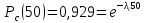







Найдем среднюю наработку до первого отказа



Средняя наработка до первого отказа равна 675 часов.

79. Приемник состоит из трех блоков: УВЧ, УПЧ и УНЧ. Интенсивности отказов этих блоков соответственно равны: λ₁=4*10^-4 1/час; λ₂=2,5*10^-4 1/час; λ₃=3*10^-4 1/час. Требуется рассчитать вероятность безотказной работы приемника при t=100 час для следующих случаев: а) резерв отсутствует; б) имеется общее дублирование приемника в целом.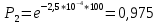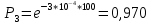









а) Р(100)=Р₁*Р₂*Р₃=0,909

б) m=2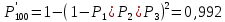





80. В радиопередатчике, состоящем из трех равнонадежных каскадов (n=3) применено общее постоянное дублирование всего радиопередатчика. Интенсивность отказов каскада равна λ=5*10^-4 1/час. Определить Р_с(t), m_tc, fc(t), λc(t) радиопередатчика с дублированием.

Р_с(t)=1-(1-e^-λnt)²

P_c(t)=

m_tc=

m_tc=

f_c(t)=2λ*e^-λt(1-e^-λt)=2*5*10^-4

λ_c(t)=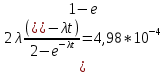