Группировка по 2 признакам, вычисление коэффициентов, графики; т. Решение в качестве группировочного признака принимаем среднегодовую стоимость основных производственных фондов

• Название: Решение в качестве группировочного признака принимаем среднегодовую стоимость основных производственных фондов
• Дата: 03.02.2021
• Размер: 142.42 Kb.
• Имя файла: Группировка по 2 признакам, вычисление коэффициентов, графики; т.docx
• Тип: Задача; #173678

Задача №1

Из годовых отчётов строительных фирм получены следующие данные о среднегодовой стоимости основных производственных фондов (млн. руб. см. ниже) и стоимости выпуска продукции (млн. руб. см. ниже)

С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов (ОПФ) и стоимостью выпуска продукции (ПР) необходимо произвести группировку фирм по среднегодовой стоимости производственных фондов. По каждой группе и совокупности фирм рассчитать:

1) число фирм;

2) среднегодовую стоимость основных производственных фондов (ОПФ);

3) стоимость продукции (ПР);

4) среднегодовую стоимость основных производственных фондов на одну фирму;

5) стоимость продукции на одну фирму;

6) стоимость продукции на 1 руб. основных производственных фондов (фондоотдачу).

Решение:

В качестве группировочного признака принимаем среднегодовую стоимость основных производственных фондов.

Число групп определяем по формуле Стерджесса: =1+3,322lgN=1+3,221lg30=6

Определяем величину интервала:

=(9-0,5)/6=1,42

(

группа 0.5+1,42=1,92

группа 1,92+1,42=3,34

группа 3,34+1,42=4,76

группа 4,76+1,42=6,18

группа 6,18+1,42=7,6

группа 7,6+1,42=9,02

Таблица 1

Исходные данные

Фирмы	ОПФ	ПР
1	3,4	3,5
2	3,1	3,3
3	4,1	4,5
4	5,8	7,5
5	5,2	6,9
6	3,8	4,3
7	4,1	5,9
8	5,6	4,8
9	4,6	5,8
10	4,2	4,6
11	6,1	8,4
12	6,5	7,3
13	1,5	2,1
14	6,4	7,8
15	7,5	10,6
16	5,1	5,8
17	4,9	5,3
18	5,8	6
19	2,8	2,5
20	2,2	1,9
21	1	1,5
22	8	8,5
23	7,7	8
24	6,3	6,5
25	5	4,5
26	1,7	2,4
27	4,1	5,1
28	0,5	1,2
29	8,2	9,9
30	9	11,3

Таблица 2

Ранжированный ряд.

ОПФ	ПР
0,5 1 1,5 1,7	1,2 1,5 2,1 2,4
2,2 2,8 3,1	1,9 2,5 3,3
3,4 3,8 4,1 4,1 4,1 4,2 4,6	3,5 4,3 4,5 5,1 5,9 4,6 5,8
4,9 5 5,1 5,2 5,6 5,8 5,8 6,1	5,3 4,5 5,8 6,9 4,8 7,5 6 8,4
6,3 6,4 6,5 7,5	8,5 7,8 7,3 10,6
7,7 8 8,2 9	8 8,5 9,9 11,3

. Среднегодовая стоимость основных производственных фондов:

Σ ОПФ

. Стоимость продукции:

Σ ПР

. Среднегодовая стоимость основных производственных фондов на одну фирму:

Σ ОПФ/n

. Стоимость продукции на одну фирму:

Σ ПР/n

. Фондоотдача:

Σ ПР/n: Σ ОПФ/n

группа: 1,8/1,175=1,53

группа: 2,6/2,7=0,95

группа: 4,81/4,04=1,19

группа: 6,15/5,44=1,13

группа: 8,55/6,675=1,28

группа: 9,425/8,225=1,15

Таблица 3

Результаты группировки

Номер группы	Группы фирм по среднегодовой стоимости ОПФ	Число фирм	Среднегодовая стоимость ОПФ	стоимость продукции	Среднегодовая стоимость ОПФ на 1 фирму	Стоимость продукции в среднем на 1 фирму	Фондоотдача
1	2	3	4	5	6	7	8
1	0,5-1,92	4	4,7	7,2	1,175	1,8	1,53
2	1,92-3,34	3	8,1	7,7	2,7	2,6	0,95
3	3,34-4,76	7	28,3	33,7	4,04	4,81	1,19
4	4,76-6,18	8	43,5	49,2	5,44	6,15	1,13
5	6,18-7,6	4	26,7	34,2	6,675	8,55	1,28
6	7,6-9,02	4	32,9	37,7	8,225	9,425	1,15

Рисунок 1 - Гистограмма распределения


Рисунок 2 - Полигон распределения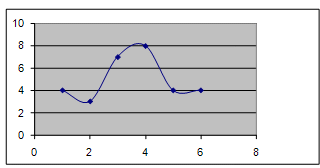


Рисунок 3 - Кумулята

Вывод: Разбив неоднородную совокупность из 30 фирм на 6 групп с равным интервалом по признаку среднегодовой стоимости ОПФ. Самая многочисленная группа 4 (8 фирм) и которая примерно равна 27%, а самая малочисленная 2 (3 фирмы) и примерно равна 10%.

Задача№2.

По данным ряда динамики об объемах строительно-монтажных работ (СМР) (тыс.руб.), выполненных строительными организациями за пятилетний период (исходные данные представлены в табл. 3), вычислить:

1. 
   абсолютные приросты (или снижения) - цепные и базисные
   
2. 
   темпы роста (или снижения) - цепные и базисные;
   
3. 
   темпы прироста (или снижения) - ценные и базисные;
   
4. 
   абсолютное содержание 1% прироста (или снижения). Полученные данные по пунктам 1-4 представить и табл. 4.
   
5. 
   среднегодовой объём работ;
   
6. 
   средний абсолютный прирост.
   
7. 
   среднегодовой темп роста и прироста (или снижения).
   
8. 
   Построить график динамики объёмов строительных работ и сделать выводы.
   

Решение:

Таблица 5

Результаты расчета

Год	Объем работ (тыс.руб.)	Абсолютный прирост (тыс.руб.)		Темп роста (%)		Темп прироста (%)		Абсод. 1%прироста (тыс.руб.)
		базисный	цепной	базисный	цепной	базисный	цепной
1	28	-	-	-	-	-	-	-
2	35	7	7	125	125	25	25	0,28
3	41	13	6	146,4	117,1	46,4	17,1	0,35
4	47	19	6	167,9	114,5	67,9	14,6	0,41
5	51	23	4	182,1	108,5	82,1	8,5	0,47
Итого	202

1. Определяем базисный и цепной абсолютные приросты по формулам:

риация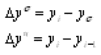



=35-28=7 (шт.)

=41-28=13

=47-28=19

=51-28=23

=35-28=7

=41-35=6

=47-41=6

=51-47=4

где yi - изучаемый уровень ряда;б - уровень ряда, принятого за базисный;- уровень ряда, предшествующий изучаемому.

. Рассчитываем базисный и цепной темпы роста:



















. Определяем базисный и цепной темпы прироста:

Тп=Тр-100%

125%-100%=25%

146,4%-100%=46,4%

167,9%-100%=67,9%

182,1%-100%=82,1%

=125%-100%=25%

=117,1%-100%=17,1%

=114,6%-100%=14,6%

=108,5%-100%=8,5%

. Находим абсолютное содержание одного процента прироста: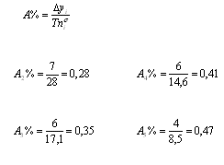



. Вычисляем среднегодовой объем работ:



6. Рассчитываем средний абсолютный прирост:



. Находим средний темп роста: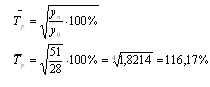



. Определяем средний прирост: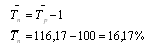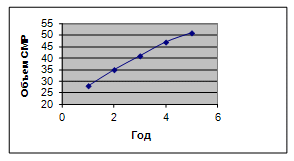




Рисунок 4 - Динамика объемов строительных работ

Вывод: На графике виден стабильный рост по годам объема строительно-монтажных работ, выполненных строительными организациями за 5 лет.

Задача №3

Для изучения дневной выработки рабочих предприятия была проведена 10%-я бесповторная выборка, в результате которой получены исходные данные о распределении рабочих по производительности труда, представленные в таблице.

Таблица 5

Исходные данные

Группа рабочих с дневной выработкой изделий, штук	Число рабочих, чел.
10-20	5
20-30	10
30-40	40
40-50	27
50-60	10
Итого	92

На основе приведенных данных вычислить:

1) среднедневную выработку рабочего;

2) дисперсию и среднеквадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,954 предельную ошибку выборки и возможные границы, в которых ожидается среднедневная выработка всех рабочих строительного предприятия.

Решение.

Таблица 7

х	f	хi	хi·fi
10-20	5	15	75	-23	529	2645
20-30	10	25	250	-13	169	1690
30-40	40	35	1400	-3	9	36
40-50	27	45	1215	7	49	1327
50-60	10	55	550	17	289	2890
Итого	92	175	3490			8588

1. Определяем среднедневную выработку рабочих: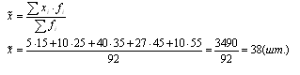



2. Вычисляем дисперсию: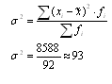



3. Рассчитываем среднеквадратическое отклонение:



4. Находим коэффициент вариации по формуле: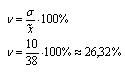



5. Определяем среднюю ошибку выборки по формуле: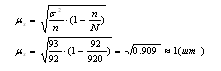



где п - число рабочих выборочной совокупности, чел.

6. Определяем предельную ошибку выборки по формуле: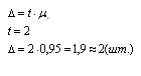



7. Находим границы среднедневной выработки генеральной совокупности: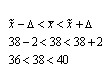



Вывод: Среднедневная выработка рабочего равна 38шт.

Среднее значение выработки одного рабочего строительного предприятия находится в пределах от 36,1 до 39,9, при вероятности p=0,954. Таким образом среднедневная выработка как раз находится в пределах 36,1-39,9.

Задача №4

По данным о продаже жилья строительным предприятием, определить:

1. Общий индекс физического объема товарооборота (количество проданных квадратных метров жилья) в декабре к январю.

2. Среднее изменение цен на жилье, если известно, что товарооборот в фактических ценах за этот период вырос в 2,7 раза.

3. Сделать выводы.

Обозначения:

а) А, Б, С – сданные в эксплуатацию жилые дома;

б) графа № 1 (по каждому варианту) – объём продажи жилья в январе текущего года (тыс. руб.);

с) графа № 2 (по каждому варианту) – изменение количества продажи жилья в декабре по отношению к январю в текущем году в %.

	р0 g0	Яg %	Яg	Р1 g1
А	220	50	1,5	594
В	480	+40	1,4	1296
С	350	-10	0,9	945
Итого	1050			2835

Решение:

Определяем общий индекс текущего товарооборота ( ) по формуле: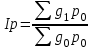
,
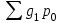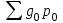где – товарооборот жилья текущего периода по ценам базисного периода, руб.; – фактический товарооборот жилья базисного периода, руб.

Ip=1317/(1,5*220+1,4*480+0,9*350)=1317/1050=1,25*100%=125%.

Определяем индекс цен ( ) по формуле: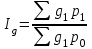

где – фактический товарооборот жилья текущего периода, руб.
р₀*g₀*2,7=р₁*g₁=1050*2,7=2835;

=(594+1296+945)/1317= 2835/1317=2,15;

2,15*100 %= 215%-100%=115%.

Вывод: Объем продаж в среднем по совокупности увеличился на 125%.

Цены выросли в среднем по всем долгам на 115%.