Кейс-Задачи. Макар О.Я. ИБ-71з - Copy. Решение Вероятность безотказной работы рассчитывается по формуле где с
 Скачать 37.92 Kb. Скачать 37.92 Kb.
|
|
Задача №1 При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t) ≥ 0,97. Исходные данные: 1.Проектируемая система состоит из n =750элементов. 2.Средняя интенсивность отказов для элементов – λ=1,75·10-6 1/ч 3.Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. 4. Заданное время работы t=150 ч Определить: 1.Вероятность безотказной работы заданной системы. 2.Как следует изменить количествоэлементов системы, чтобы надежность системы удовлетворяла поставленным требованиям? 3.Как следует изменить надежностьэлементов системы, чтобы надежность всей системы удовлетворяла поставленным требованиям? 4.Как следует изменить время работысистемы, чтобы надежность системы удовлетворяла поставленным требованиям Решение Вероятность безотказной работы рассчитывается по формуле: 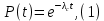 где λс - интенсивность отказов системы, 1/ч Интенсивность отказов системы λс , 1/ч ,учитывая равнонадежность всех 350 элементов, определим по формуле: λс =λ ∙n, (2) где λ - средняя интенсивность отказов элемента, 1/ч ; λ =1,75∙10-6 1/ч. n – количество элементов в системе, n =750 Тогда по формуле (1) для t =150ч 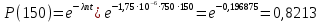 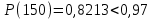 Полученная оценка значения вероятности безотказной работы не удовлетворяет заданным требованиям. Необходимо определить значения переменных n, λ и t , при которых будет выполняться неравенство: 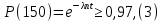 После логарифмирования обеих частей неравенства получим 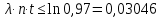 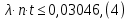 Из неравенства (4) можно определить, что выполнение заданного требования по значению надежности 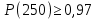 возможно, если переменные λ, n, t (при прочих равных условиях) будут принимать следующие значения: возможно, если переменные λ, n, t (при прочих равных условиях) будут принимать следующие значения: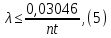 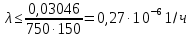 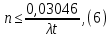 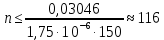 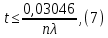 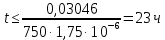 Полученные результаты показывают, что для ого, чтобы удовлетворить требованиям по вероятности безотказной работы проектируемой системы необходимо: - при заданных значениях n =750элементов и t =150 ч построить систему, используя элементы, для которых значение интенсивности отказов не превышает значения 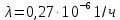 ; ;- при заданных значениях 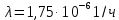 и t =150 ч построить систему не более, чем из 116 элементов; и t =150 ч построить систему не более, чем из 116 элементов;- при заданных значениях 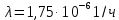 и n =750элементов обеспечить функционирование системы не более 23 часов. и n =750элементов обеспечить функционирование системы не более 23 часов.Задача №2 При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t) ≥ 0,97. Исходные данные: 1. Проектируемая система состоит из n =750элементов. 2. Средняя интенсивность отказов для элементов – λ=1,75·10-6 1/ч 3. Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Определить: Кратность резервирования всей системы, обеспечивающую требуемое значение вероятности безотказной работы (P(t)). Решение Вероятность безотказной работы системы с общим постоянно включенным резервированием можно определить по формуле : 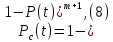 где P 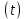 - вероятность безотказной работы исходной системы; - вероятность безотказной работы исходной системы;m – кратность резервирования . Для определения значения m подставим известные значения 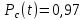 ( по заданию) и P ( по заданию) и P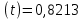 (задача 1) в формулу (8) и получим: (задача 1) в формулу (8) и получим: 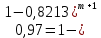 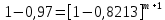 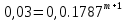 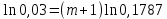 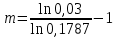 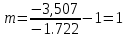 Подставляем полученное значение m=1 в формулу (8): 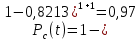 Полученный результат не удовлетворяет поставленному требованию: 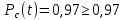 . Таким образом, в рассматриваемом случае необходимый уровень надежности можно обеспечить дублированием - добавлением (параллельным подключением) к существующей системе одной резервной. . Таким образом, в рассматриваемом случае необходимый уровень надежности можно обеспечить дублированием - добавлением (параллельным подключением) к существующей системе одной резервной.Задача №3 При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t) ≥ 0,97. Исходные данные: 1.Проектируемая система состоит из n =750элементов. 2.Средняя интенсивность отказов для элементов – λ=1,75·10-6 1/ч 3.Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Определить: Кратность поэлементного резервирования системы, обеспечивающую требуемое значение вероятности безотказной работы (P(t)). 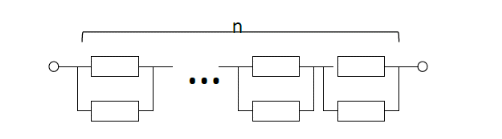 Рисунок 1 – Структура системы при поэлементном резервировании системы Решение Вероятность безотказной работы системы при поэлементном (раздельном ) резервировании , при равнонадежных элементах и одинаковой кратности их резервирования определяется по формуле: 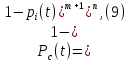 где 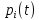 - вероятность безотказной работы i–го элемента системы - вероятность безотказной работы i–го элемента системыВероятность безотказной работы i–го элемента рассчитывается по формуле: 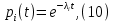 где λi - интенсивность отказов i–го элемента системы, 1/ч Дляt =150 ч и λ = 1,75·10-6 1/ч 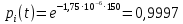 Для определения значения m подставим известные значения n=750 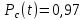 ( по заданию) и ( по заданию) и 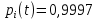 в формулу (9) и получим: в формулу (9) и получим: 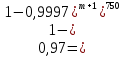 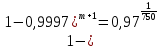 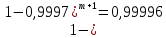 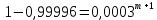 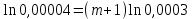 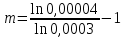 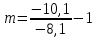 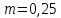 Принимается m=1 Подставляем полученное значение m=1 в формулу (9): 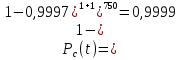 Полученный результат удовлетворяет поставленному требованию: 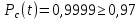 . Таким образом, в рассматриваемом случае необходимый уровень надежности можно обеспечить поэлементным резервированием - добавлением (параллельным подключением) к каждому элементу существующей системы по одному резервному. . Таким образом, в рассматриваемом случае необходимый уровень надежности можно обеспечить поэлементным резервированием - добавлением (параллельным подключением) к каждому элементу существующей системы по одному резервному.Задача №4 При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t) ≥ 0,97. Исходные данные: 1.Проектируемая система состоит из n =750элементов. 2.Средняя интенсивность отказов для элементов – λ=1,75·10-6 1/ч 3.Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Определить: 1. Состав нерезервируемых (nнр) и резервируемых ( nр) структурных элементов системы при резервировании части которой ( nр), выполняются требования по надежности проектируемой системы. 2. Кратность резервирования nр-части системы 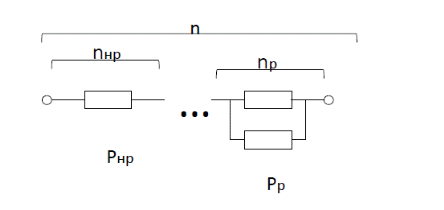 Рисунок 2 - Структура системы при частичном резервировании системы Решение Рассматриваемая система может быть представлена как система, сотоящая из двух последовательно соединенных участков - нерезервированного и резервированного. При последовательном соединении участков общая надежность системы будет определяться наиболее слабым звеном , поэтому при проектном расчете используем принцип равнонадежности , то есть примем равными надежности нерезерированного (PНР) и резервированного участков (PР) : PНР(t) =PР(t) . Соответственно, вероятность безотказной работы всей системы можно записать в следующем виде: 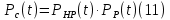 Тогда 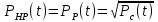 (12) (12)Подставив заданное значение Pc(t)=0,97, получим 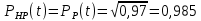 Определим количество элементов нерезвированного участка nНР из формулы для определения вероятности безотказной работы последовательного соединения равнонадежных элементов: 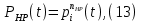 где 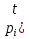 ) – вероятность безотказной работы i –го элемента ) – вероятность безотказной работы i –го элемента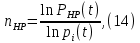 Подставив в формулу (14) значения 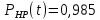 и и 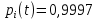 (определенное ранее по формуле (10)), получим (определенное ранее по формуле (10)), получим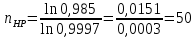 Принимается 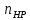 = 50 = 50Подставив 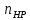 = 50 формулу (12), получим = 50 формулу (12), получим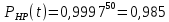 Определяется количество элементов резервированного участка nР : 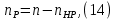 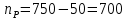 Вероятность безотказной работы резервированного участка до резервирования 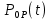 рассчитывается по формуле (13): рассчитывается по формуле (13):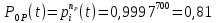 Определяется кратность резервирования m из формулы (8) для оценки вероятности безотказной работы системы с общим постоянно включенным резервированием. Для определения значения m подставим проектное значение 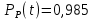 и полученное и полученное 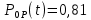 в формулу (8) и получим: в формулу (8) и получим: 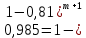 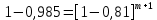 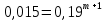 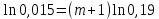 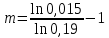 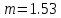 Принимается m=2 Определяется вероятность безотказной работы резервированного участка системы с кратностью m=1 по формуле (8): 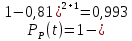 Вероятность безотказной работы всей системы определяется по формуле (11): 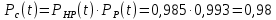 Полученный результат удовлетворяет поставленному требованию: 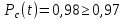 . . 1.Выполнение поставленного требования по надежности проектируемой системы 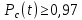 обеспечивается при следующем составе структурных элементов : обеспечивается при следующем составе структурных элементов :количество нерезервируемых элементов 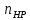 = 50; = 50;количество резервируемых элементов 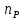 = 700. = 700. 2. Кратность резервирования 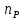 -части системы, состоящей из 700 элементов, m =2. -части системы, состоящей из 700 элементов, m =2. |
