Решение Выделим в корне целую часть 19 2 361 20 2 400 Тогда
 Скачать 89.77 Kb. Скачать 89.77 Kb.
|
|
1. Представить 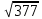 в виде периодической цепной дроби и вычислить с точностью до ε = 10−5. в виде периодической цепной дроби и вычислить с точностью до ε = 10−5.Решение Выделим в корне целую часть: 192 = 361; 202 = 400 Тогда: 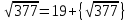 Преобразуем дробную часть в дробь с числителем 1: 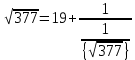 Избавимся от иррациональности в знаменателе дроби: 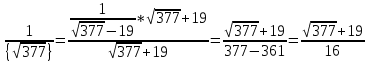 Выделим целую часть: 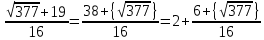 То есть, 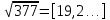 Цепная дробь: 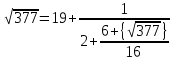 Перевернем дробную часть: 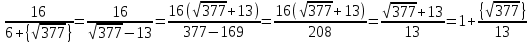 То есть, 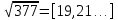 Цепная дробь: 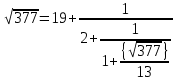 Перевернем дробную часть: 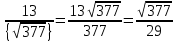 То есть, 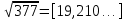 Цепная дробь: 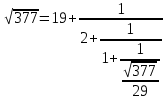 Перевернем дробную часть: 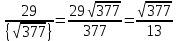 Такая дробь была получена на предыдущем шаге, значит, процесс разложения окончен. Ответ: 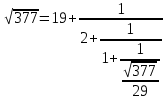 2. Найти остаток от деления 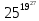 на 84. на 84.Решение 3. Найти наименьшее натуральное число x, удовлетворяющее условиям: x ≡ 12 mod 27, x ≡ 36 mod 37, x ≡ 6 mod 22, x ≡ 9 mod 13 Решение Имеем систему сравнений первой степени с взаимно простыми модулями. Найдем М = 27*37*22*13 = 285714 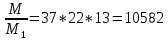 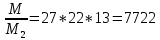 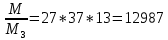 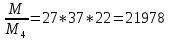 Тогда получим систему уравнений: 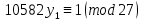 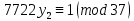 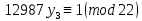 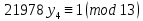 Запишем ее в следующем виде: 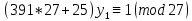 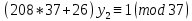 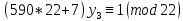 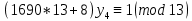 Так как am+b 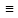 b (mod m), то система примет вид: b (mod m), то система примет вид: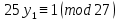 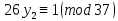 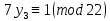 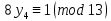 Решая ее, получим: 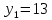 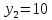 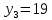 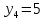 Тогда решение исходной системы будет иметь вид: x ≡ 12*13*10582 + 36*10*7722 + 6*19*12987 + 9*5*21987 (mod 285714) Или x ≡ 6900645 (mod 285714) ≡ 43509 (mod 285714) 4. Пусть m = 35 и e = 7 открытая часть ключа RSA. Найти закрытую часть ключа d. 5. Сколько целых слагаемых содержит бином 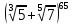 Решение Воспользуемся формулой: 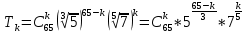 Полученное выражение будет рациональным, если 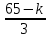 и и 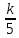 – целые числа. – целые числа.Число k будем искать среди чисел, кратных 5 и 1 ≤ k ≤ 65. Всего таких чисел: 65/5 + 1 = 14 Ответ: 14 6. Пусть имеется 6 кодовых символов: D,E,N, T, S, U с частотами появления:
C помощью алгоритма Хаффмена построить код Шеннона-Фэно для текстового сообщения STUDENT (большему слову приписываем справа 1, а меньшему – 0). Решение Упорядочим символы алфавита в порядке убывания вероятности их появления:
Составим таблицу:
Тогда получим: STUDENT = 111 011 001 00 10 101 011 7. Найти решение однородного рекуррентного уравнения с граничными условиями: 3fn+2 − 8fn+1 + 4fn = 0, f0 = 2, f1 = 2. 8. Используя граф на рис. 2.1 (источник вершина A), проиллюстрировать алгоритм просмотра вершин графа и построения остовного дерева: (a) в глубину; (b) в ширину. В решении указать порядок просмотра вершин графа, динамику изменения состояния стека и очереди, маркировку вершин. Решение проиллюстрировать рисунком. 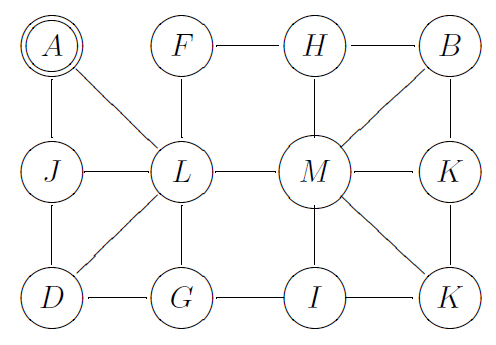 9. Построить Эйлеров путь в графе, заданном своей матрицей смежности:
10. Найти незамкнутый маршрут минимальной длины методом ветвей и границ для графа на рис. 2.2. Представить частичные решения (в форме остовных деревьев) и их расширения. 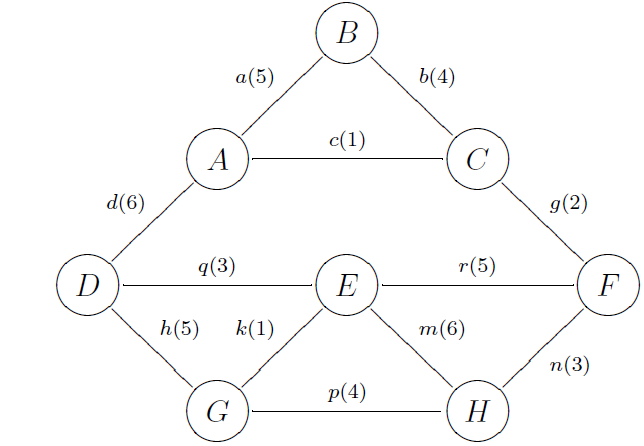 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
