Практическая работа по дисциплине Статистика. Практическая работа по дисциплине Статистика Соболевой Е.Е. Решение Выработка на одного работающего количества произведенной продукции
 Скачать 332.24 Kb. Скачать 332.24 Kb.
|
Практическое задание
дисциплине
Пермь 2020  Решение: Выработка на одного работающего количества произведенной продукции: В=К/( Ч) Выработка для каждого завода:
Величина интервала: i=(Xmax-Xmin)/( n) , где X max и X min – максимальное и минимальное значения признака т.е. число рабочих, а n – число групп. i=(1900-700)/( 3)=400 - получили 3 группы: 1гр. - от 700 до 1100 рабочих 2 гр. – от 1100 до 1500 рабочих 3 гр. – от1500 до 1900 рабочих Рабочая таблица:
По данным рабочей таблицы составляем аналитическую группировку:
Вывод: с увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего. 3адача 2. Выпуск продукции на заводе в 2018 г. составил 160 млн. руб. По плану на 2019 г. предусматривалось выпустить продукции на 168 млн. руб., фактически же выпуск составил 171,36 млн. руб. Вычислите относительные величины планового задания и выполнения плана. Решение: На основе имеющихся данных рассчитаем относительные показатели: - относительная величина планового задания: ОВПЗ = ВП1пл : ВП0ф * 100% = 168 : 160 * 100% = 105% - относительная величина выполнения плана: ОВВП = ВП1ф : ВП1пл * 100% = 171,36 : 168 * 100% = 102% Вывод: в 2019 году планировалось увеличить объем производства продукции на 5% по сравнению с 2018 г., по итогам года план производства продукции был перевыполнен на 2%.  Решение: Узнаем количество работников в цеху: Цех 1 – 600*3=1800 Цех 2 – 800*3=2400 Цех 3 – 400*2=800 Цех 4 – 200*1=200 Количество работников на заводе: Цех 1+ Цех 2 + Цех 3 + Цех 4 1800 + 2400 + 800 + 200 = 5200 Количество работников работающих по 8 часов: 1800 + 2400 + 800 = 5000 (96,2%) Количество работников работающих по 6 часов: 200 (3,2%) Средняя продолжительность смены: 8*96,2%+6*3,2% = 7,696+0,192=7,888 часа. Ответ: средняя продолжительность смены 7,888 часа.  Среднюю месячную зарплату определяем по формуле:  , где , где - середина i-го интервала, - середина i-го интервала, - число рабочих в середине i-го интервала. - число рабочих в середине i-го интервала. , , , , , , , ,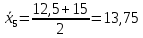 , , . .Следовательно, средняя месячная зарплата рабочих цеха составляет 10,083 тыс. руб. Так как ряд имеет равные интервалы, то мода находится в интервале с наибольшей частотой, то есть в интервале 10,0 - 12,5 тыс. руб. Следовательно, её можно вычислить по формуле:  , где , где - нижняя граница модального интервала, - нижняя граница модального интервала,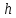 - величина модального интервала, - величина модального интервала, - частота модального периода, - частота модального периода, - частота предмодального периода, - частота предмодального периода, - частота постмодального периода. - частота постмодального периода. . .Следовательно, наиболее часто встречающаяся заработная плата 11, 333 тыс. руб. Определим медиану по формуле:  , где , где - нижняя граница медианного периода, - нижняя граница медианного периода,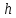 - величина медианного периода, - величина медианного периода, - частота медианного периода, - частота медианного периода,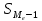 - накопленная частота предмедианного периода. - накопленная частота предмедианного периода. . .Дисперсию можно определить по формуле:  , , , , , , . .Среднеквадратическое отклонение:  , , . .Коэффициент вариации:  , , , , , следовательно, выборка однородная. , следовательно, выборка однородная.Задача 5. Объем продукции на промышленном предприятии повысился в 2013 году по сравнению с 2008 годом на 100 млн. рублей в сопоставимых ценах, или на 25%. В 2018 году объем продукции увеличился по сравнению с 2013 годом на 20%. Определите: 1) объем выпуска продукции предприятия в 2008, 2013, 2018 годах; 2) среднегодовые темпы прироста выпуска продукции за: а) 2008-2013 гг.; б) 2013-2018 гг.; в) 2008-2018 гг. Решение. Определим: 1) объем выпуска продукции предприятия: - 2008 год: ВП2008 = 100 / 0,25 = 400 млн. руб. - 2013 год: ВП2013 = 400 + 100 = 500 млн. руб. - 2018 год: ВП2018 = 500 * (1 + 0,2) = 600 млн. руб. 2) среднегодовые темпы прироста выпуска продукции за: а) 2008-2013 гг.: или 103,8% б) 2013-2018 гг.: или 103,1% в) 2008-2018 гг.: или 103,75% Вывод: в 2008 - 2013 гг. объем выпуска продукции на промышленном предприятии ежегодно увеличивался в среднем на 3,8%, в период с 2013 г. по 2018 г. ежегодный темп прироста выпуска продукции составлял 3,1%, а в целом за период с 2008 г. по 2018 г. объем выпуска продукции на промышленном предприятии ежегодно увеличивался в среднем на 3,75%. Задача 6. По одному из предприятий промышленности стройматериалов имеются следующие данные:
Определите общий индекс цен и сумму роста или снижения объема реализации продукции за счет изменения цен. Решение: Общий индекс цен: Ig= 100 – 2 = 98% = 0.98 Ig = 100+5 = 105% = 1.05 I = p1g1|ig*p0g0 1960+2100+440/0.98*1960 +1.05*2100+1*440 = 4500/1920.8+2205+440 = 0.986 = 98.6% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
