КР по абстрактной алгебре. АА-2019-в3. Решение Воспользуемся теорией сравнений. Имеем Так как, то сравнение имеет единственное решение. Имеем
 Скачать 1.9 Mb. Скачать 1.9 Mb.
|
№1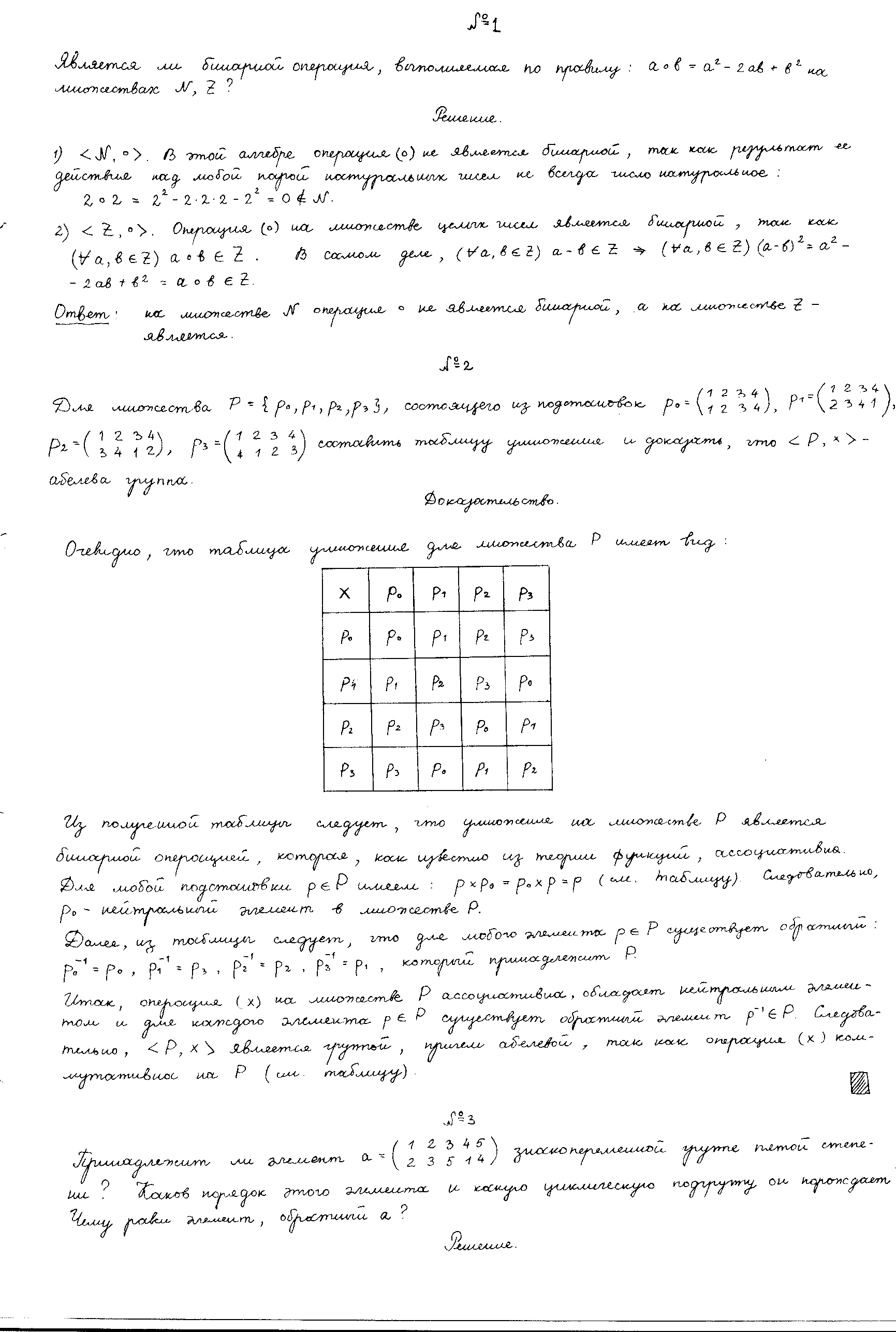 №2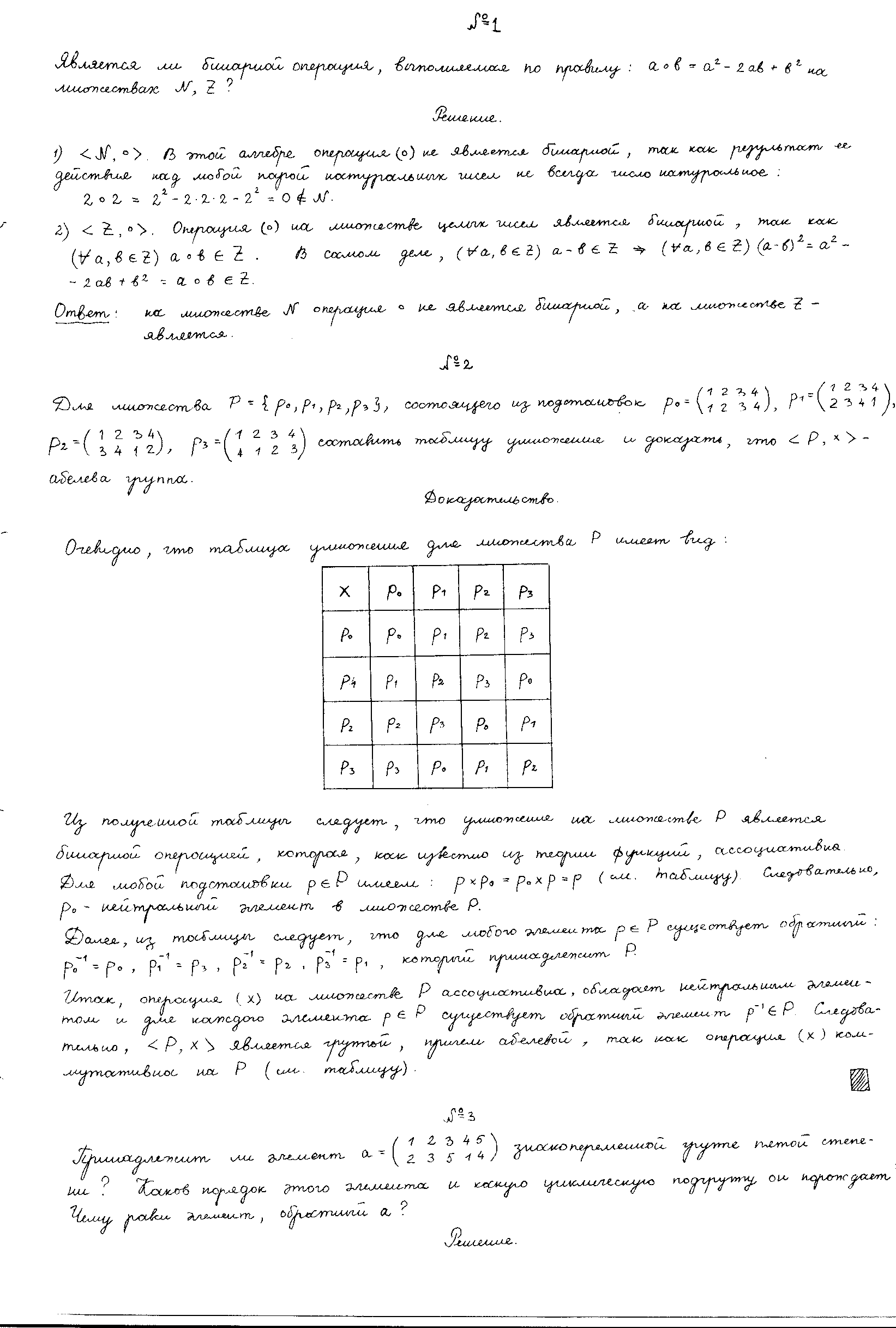 №3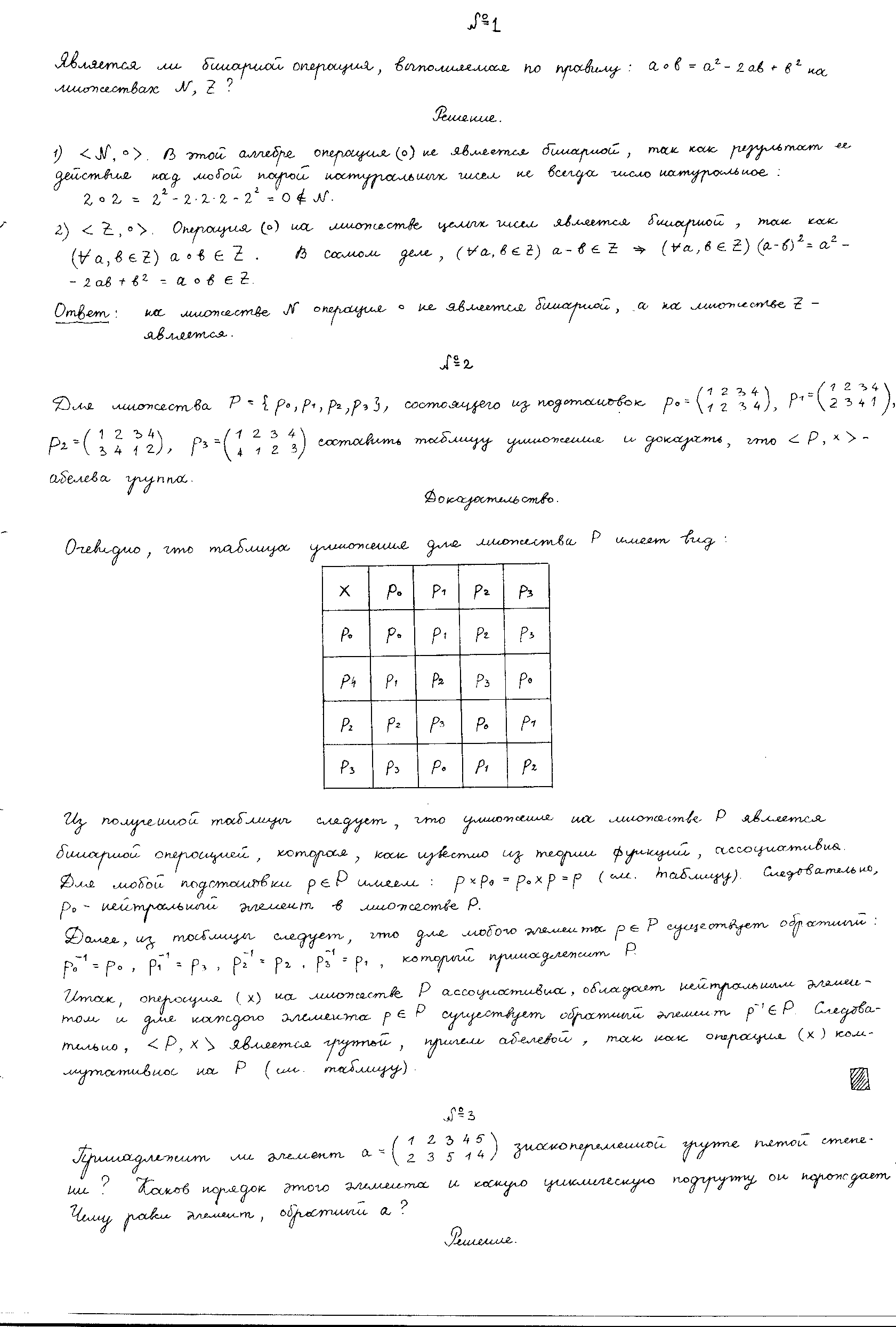  №4 №5 №6Является ли гомоморфизмом отображение 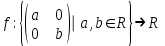 , если , если 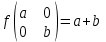 ? ?Решение Очевидно, что отображение 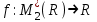 , , 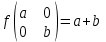 , , 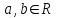 не является гомоморфизмом, так как не сохраняет умножение. Действительно, если не является гомоморфизмом, так как не сохраняет умножение. Действительно, если 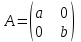 и и 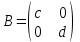 – любые элементы из множества – любые элементы из множества 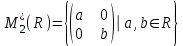 , то и , то и 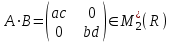 . Отсюда получаем: . Отсюда получаем: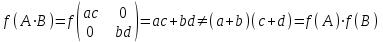 . .Ответ: f не является гомоморфизмом. №7 (1 способ)Найти общее решение уравнения первого порядка 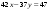 . .Решение Воспользуемся теорией сравнений. Имеем: 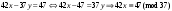 . .Так как 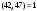 , то сравнение имеет единственное решение. , то сравнение имеет единственное решение.Имеем: 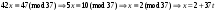 , где t – любое целое число. , где t – любое целое число.Отсюда получаем: 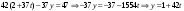 . .Ответ: 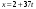 , , 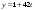 , где t – любое целое число. , где t – любое целое число.№7 (2 способ)Решить уравнение в целых числах: 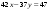 . .Решение Разложим 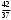 в цепную дробь: в цепную дробь:
т. е. 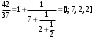 . .Составим все подходящие дроби: 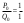 ; ; 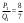 ; ; 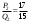 ; ; 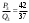 . .На основании свойства подходящих дробей 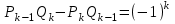 получим: 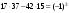 или или 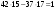 . .Умножив обе части равенства на 47, находим: 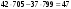 , ,то есть 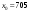 , , 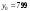 – частное решение данного уравнения. – частное решение данного уравнения.Все решения могут быть найдены по формулам: 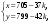 или (при или (при 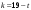 ) ) 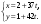 Ответ: 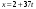 , , 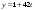 , где t – любое целое число. , где t – любое целое число.№8Найти все целые решения уравнения второго порядка 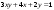 . .Решение Умножим обе части данного уравнение на 3 и преобразуем его: 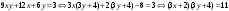 . .Решим в целых числах уравнение: 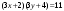 . .Так как целыми делителями числа 11 являются числа 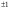 и и 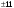 , то множество всех целочисленных решений полученного уравнения содержится в множестве целочисленных решений следующих четырех систем: , то множество всех целочисленных решений полученного уравнения содержится в множестве целочисленных решений следующих четырех систем:1) 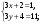 2) 2) 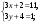 3) 3) 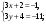 4) 4) 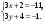 Только две системы (2-я и 3-я) имеют решения в целых числах. Следовательно, множество целых решений уравнения второго порядка 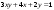 имеет вид: имеет вид: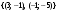 . .Ответ: 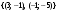 . . |
