численные методы. Вариант 2. Решение Введем следующие обозначения z 1 ab, z 2 е х, z 3 z
 Скачать 38.4 Kb. Скачать 38.4 Kb.
|
|
Вариант 2 Задание 1. Задание:Даны a, b, y – приближенные числа с верными значащими цифрами, х – точное число. Вычислите 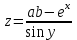 и оцените погрешность результата. и оцените погрешность результата.
Решение Введем следующие обозначения: z1 ab, z2 ех, z3 z1 z2, z4 sin y, 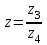 . .Заполним таблицу 1, определив абсолютные погрешности исходных данных по известным верным значащим цифрам. Абсолютная погрешность измерения 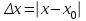 Относительная погрешность: 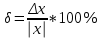 Таблица 1
Оценим погрешности z1 ab, взяв для этого две-три значащие цифры произведения. Затем найдите верные значащие цифры z1 и запишите ответ с одной сомнительной цифрой. Вычислим z2 ехи округлите его при необходимости так, чтобы погрешность округления не оказала существенного влияния на точность дальнейших расчетов. Продолжим таким же образом вычисления дляz3, z4 и z. Результаты расчетов расположим в таблице 2. Относительную погрешность сумм, разностей, произведений и частных рассчитываем как сумму соответствующих погрешностей Таблица 2
Исходя из рассчитанной погрешности, видим, что значащими являются первые 2 цифры после запятой результата, а относительная погрешность вычислений составляет не более 0,266% Таким образом, 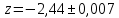 Задание 2. Задания: а) Отделите графически один из корней заданного уравнения и определите его с точностью 0,5 10 – 3 методом простой итерации. а) ln x 2x 0; б) Отделите аналитически один из корней заданного уравнения и определите его с точностью до 0,5 10 –3 комбинированным методом хорд и касательных. б) x3 3x2 24x 10 0 Решение А) изобразим графически 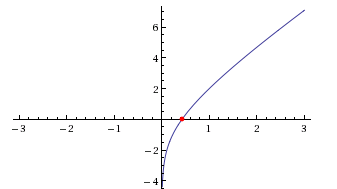 Корень в интервале (0,1;0,7) Представим уравнение в форме: x = x - λ(2•x+ln(x)) Найдем максимальное значение производной от функции f(x) = 2•x+ln(x) y = 2+1/x [0.1;0.7] Необходимое условие экстремума функции одной переменной. Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает. Достаточное условие экстремума функции одной переменной. Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: f'0(x*) = 0 f''0(x*) > 0 то точка x* является точкой локального (глобального) минимума функции. Если в точке x* выполняется условие: f'0(x*) = 0 f''0(x*) < 0 то точка x* - локальный (глобальный) максимум. Находим первую производную функции: y' = -1/x2 Приравниваем ее к нулю: -1/x2 = 0 Глобальных экстремумов нет Находим стационарные точки: Вычисляем значения функции на концах отрезка f(0.1) = 12 f(0.7) = 3.4286 Ответ: Имеются только локальные экстремумы (на заданном интервале) fmin = 12, fmax = 3.43 max(dF/dx = 2+1/x) ≈ 0 Значение λ = 1/(0) ≈ 0.1 Таким образом, решаем следующее уравнение: x-0.1(2•x+ln(x)) = 0 Поскольку F(0.1)*F(0.7)<0, то корень лежит в пределах [0.1;0.7]. Остальные расчеты сведем в таблицу.
Ответ: x = 0.4257; F(x) = -0.0026 Б) Найдем корни уравнения: x3+3•x2-24•x-10 = 0 Используем для этого комбинированный метод. Пусть f(a)f(b)<0, а f’(x) и f’’(x) сохраняют знаки на [a,b]. Объединяя метод хорд и метод Ньютона, можно ускорить сходимость итерационного процесса поиска корня. В результате мы получаем комбинированный метод, на каждом шаге которого находим значение обоих границ интервалов, внутри которых содержится корень. Также как и в методе хорд, рассмотрим следующие ситуации: 1. Если f’’(b0)f(b0)>0 (то есть bn - неподвижен) то: 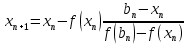 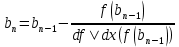 2) Если f’’(a0)f(a0)>0 (an - неподвижен), то: 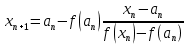 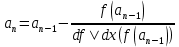 Находим первую производную: dF/dx = 3•(x2+2•x-8) Находим вторую производную: d2F/dx2 = 6•(x+1) Поскольку F(-1)*F(0)<0, то корень лежит в пределах [-1;0] Вычисляем значения функций в точке a = -1 f(-1) = 16 f ''(-1) = 0 Поскольку f(a)•f ''(a) < 0, то x0 = b = 0 Остальные расчеты сведем в таблицу.
Ответ: x = -0.3994 |
