химия. Решение Взаимный пересчет величин и производится по формулам Таким образом, получим
 Скачать 267.81 Kb. Скачать 267.81 Kb.
|
14. Определить относительную плотность нефтепродукта 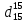 по его относительной плотности по его относительной плотности 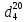 =0,709. =0,709.
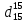 -? -?Решение Взаимный пересчет величин 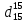 и и 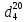 производится по формулам: производится по формулам: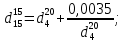 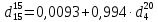 Таким образом, получим: 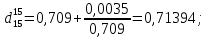 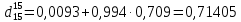 Результаты, полученные при расчете двумя способами, близки между собой. Ответ: 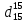 =0,71394 или =0,71394 или 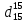 =0,71405. =0,71405.44. Относительная плотность нефтепродукта 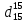 =0,920. Найти его относительную плотность при 1100С двумя способами. =0,920. Найти его относительную плотность при 1100С двумя способами.
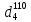 -? -?Решение Определим относительную плотность 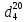 нефтепродукта: нефтепродукта: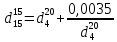 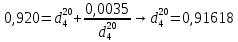 Определим относительную плотность нефтепродукта при 1100С по формуле Менделеева: 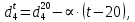 где 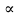 -температурная поправка; в интервале -температурная поправка; в интервале 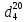 =0,9100-0,9199 =0,9100-0,9199 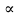 =0,000620 =0,000620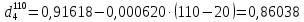 Определим относительную плотность нефтепродукта при 1100С с помощью графика (рисунок 1). 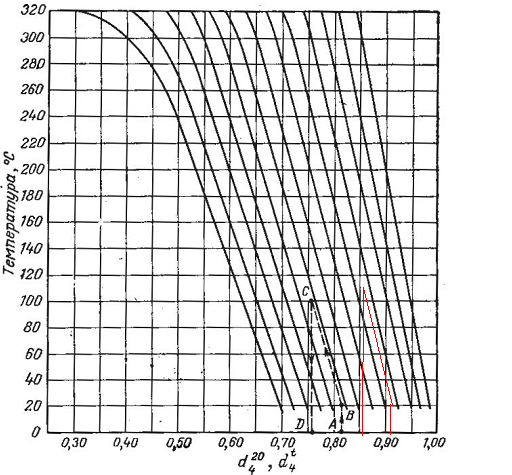 Рисунок 1 - График для определения относительной плотности жидких нефтепродуктов 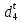 при известной их плотности при известной их плотности 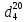 По графику находим, что 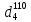 0,860 0,860Ответ: 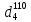 =0,86038 =0,8603874. Определить абсолютную плотность н-бутана при 1800С и 11000 кгс/м2.
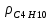 -? -?Решение Расчет выполняем по формуле: 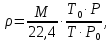 где М – молярная масса н-бутана, кг/кмоль; М (С4Н10)=58 кг/кмоль; Т0, Р0 – температура и давление, соответствующие нормальным условиям, соответственно равны 273 К и 101325 Па; Т, Р - температура и давление, соответствующие рабочим условиям, соответственно равны 273+180=453 К и 11000·9,81=107910 Па 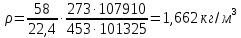 Ответ: 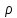 =1,662 кг/м3 =1,662 кг/м3104. Смесь узких нефтяных фракций содержит 3 компонента, содержания которых равны соответственно (% об.) 13, 17 и 70. Плотности их 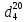 равны соответственно 0,7999; 0,8025 и 0,8064. Найти относительную плотность смеси. равны соответственно 0,7999; 0,8025 и 0,8064. Найти относительную плотность смеси.
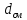 -? -?Решение Средняя относительная плотность смеси жидких компонентов определяется оп правилу аддитивности: 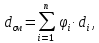 где 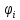 -объемная доля i-го компонента смеси; -объемная доля i-го компонента смеси;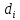 -относительная плотность i-го компонента смеси -относительная плотность i-го компонента смеси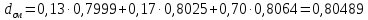 Ответ: 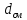 =0,80489 =0,80489134. Вычислить среднюю молекулярную массу нефтяных фракций, имеющих средние температуры кипения 100, 150 и 200. Вычислить среднюю молекулярную массу нефтяной фракции, имеющей плотность 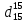 =0,7214. =0,7214.
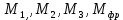 -? -?Решение Для нефтей и нефтепродуктов зависимость между молекулярной массой и средней температурой кипения имеет следующий вид (формула Бриджиман): 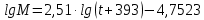 Таким образом, получим: 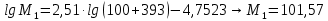 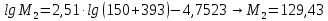 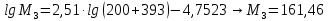 Зависимость между молекулярной массой и относительной плотностью 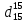 описывается формулой Крэга: описывается формулой Крэга: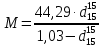 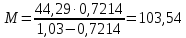 Ответ: М1=101,57; М2=129,43; М3=161,46; М=103,54 164. Определить среднюю молекулярную массу нефтепродукта, имеющего среднюю температуру кипения 3000С и относительную плотность 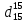 =0,94. Задачу решить двумя способами. =0,94. Задачу решить двумя способами.
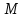 -? -?Решение Рассчитаем среднюю молекулярную массу нефтепродукта по формуле: 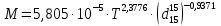 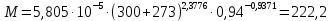 Определим среднюю молекулярную массу нефтепродукта с помощью графика (рисунок 2). 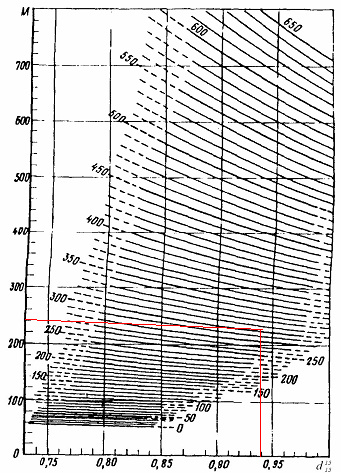 Рисунок 2 - Зависимость молекулярной массы нефтепродуктов от плотности и средней мольной температуры кипения (цифры у кривых - средние температуры кипения фракций) По графику находим М220. Ответ: М=222,2 194. Определить среднюю молекулярную массу широкой нефтяной фракции, состоящей из 31 % (масс.) бензина с молекулярной массой 112; 29 % (масс.) керосина с молекулярной массой 141 и 40 % (масс.) дизельного топлива с молекулярной массой 240.
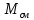 -? -?Решение Среднюю молекулярную массу смеси известного состава рассчитываем по формуле: 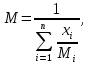 где 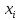 -массовая доля i-го компонента смеси; -массовая доля i-го компонента смеси;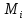 -молекулярная масса i-го компонента смеси -молекулярная масса i-го компонента смеси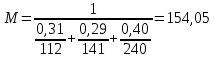 Ответ: М=154,05 224. Определить поверхностное натяжение при 200С нефтяной фракции 202–2140 С, имеющей плотность 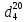 = 0,7925. Задачу решить двумя способами. = 0,7925. Задачу решить двумя способами.
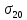 -? -?Решение Воспользуемся следующей формулой для расчета поверхностного натяжения нефтяной фракции при 200С: 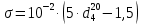 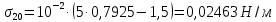 Пусть средняя температура, определенная по началу и концу кипения фракции будет среднемольной, то есть: 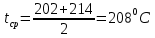 Рассчитаем молекулярную массу фракции по формуле: 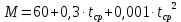 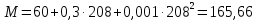 Тогда поверхностное натяжение рассматрвиаемой фракции при 200С можно определить по следующей формуле: 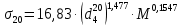 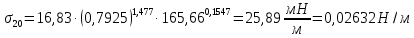 Результаты, полученные при расчете двумя способами, близки между собой. Ответ: 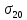 =0,02463 Н/м; =0,02463 Н/м; 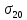 =0,02632 Н/м =0,02632 Н/м254. Кинематическая вязкость узкой нефтяной фракции при 500С равна 120,9 сСт, относительная плотность 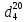 = 0,9207. Определить динамическую и условную вязкость при той же температуре. = 0,9207. Определить динамическую и условную вязкость при той же температуре.
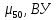 -? -?Решение Переход между кинематической и динамической вязкостью производится по формуле: 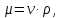 в котором все параметры должны быть опредлены при одной температуре. Значение абсолютной плотности нефтяной фракции при 500С определяем по уравнению Мановяна: 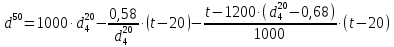 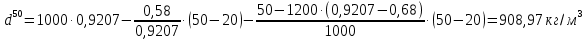 Тогда динамическая вязкость будет равна: 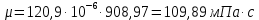 Так как 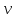 >120 сСт, то определение условной вязкости ведем по формуле: >120 сСт, то определение условной вязкости ведем по формуле: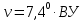 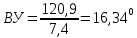 Ответ: 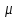 =109,89 мПа·с; ВУ=16,340. =109,89 мПа·с; ВУ=16,340.284. Кинематическая вязкость узкой нефтяной фракции при 500С равна 14,40 сСт, а при 1000С– 4,10 сСт. Определить кинематическую вязкость этой фракции при 1100С. Задачу решить двумя способами.
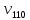 -? -?Решение Воспользуемся формулой Гросса: 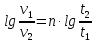 Для расчетов с её использованием сначала по двум имеющимся парам значений температура-вязкость вычислим значение коэффициента 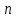 : :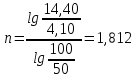 Далее, используя одну из имеющихся пар значений температура-вязкость, и заданную температуру, определим вязкость при заданной температуре: 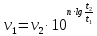 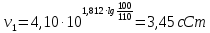 Решим эту же задачу с помощью уравнения Вальтера: 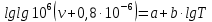 Расчет коэффициентов 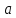 и и 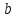 выполняем по уравнениям: выполняем по уравнениям: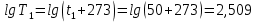 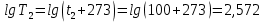 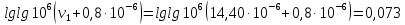 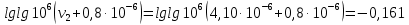 Коэффициент 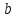 : :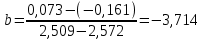 Коэффициент 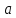 : :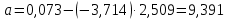 Таким образом, температурная зависимость вязкости нефтяной фракции имеет вид: 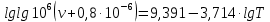 При 1100С правая часть уравнения равна: 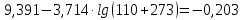 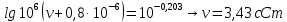 Результаты, полученные при расчете двумя способами, практически совпадают. Ответ: 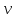 =3,45 сСт =3,45 сСт
314. Кинематическая вязкость узкой нефтяной фракции при атмосферном давлении 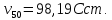 Определить вязкость дифракции при той же температуре и 18200 кгс/м2. Определить вязкость дифракции при той же температуре и 18200 кгс/м2.
344. Определить вязкость смеси, состоящей из 37% (масс.) фракции с вязкостью 35 сСт и 63% (масс.)фракции с вязкостью 90 сСт.
374. 404. 434. 464. 494. 524. 554. 584. 614. 644. 674. 704. 734. 764. 794. 824. 854. 884. 914.Определить критическую температуру и давление для фракции 28-200 °С карактайский нефти (см.усл задачи 395), имеющей плотность 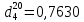 . Задачу решать всеми возможными способами. . Задачу решать всеми возможными способами.944. Определить константу фазового равновесия метана при 70°С и 4000 мм.рт.ст. 974. Рассчитать константу фазового равновесия узкой нефтяной фракции 70-88 °С плотностью 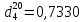 при 110°С и 800 мм.рт.ст и определить ее значение по номограмме. при 110°С и 800 мм.рт.ст и определить ее значение по номограмме. |

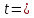 1800C
1800C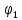 =13%
=13%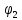 =17%
=17%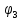 =70%
=70%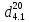 =0,7999
=0,7999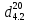 =0,8025
=0,8025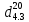 =0,8064
=0,8064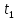 =1000С
=1000С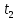 =1500С
=1500С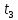 =2000С
=2000С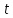 =3000С
=3000С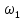 =31%
=31%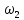 =29%
=29%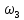 =40%
=40%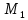 =112
=112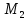 =141
=141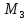 =240
=240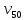 =120,9 сСт
=120,9 сСт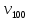 =4,10 сСт
=4,10 сСт