Физика. Решение За вторым законом Ньютона в импульсной форме Продифференцируем выражение для импульса по времени
 Скачать 182.24 Kb. Скачать 182.24 Kb.
|
|
9.1. Частица движется так, что ее радиус-вектор зависит от времени по закону 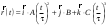 , где , где 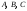 – постоянные величины, – постоянные величины, 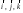 – единичные орты в декартовой системе координат. Найдите тангенс угла, под которым будет направлена скорость – единичные орты в декартовой системе координат. Найдите тангенс угла, под которым будет направлена скорость  к оси z в момент времени к оси z в момент времени 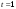 с, если с, если 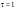 с. с.А = 4 м, В = 3 м, С = 2 м. Скорость – производная от закона по времени: 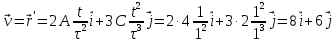  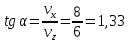 9.2. Д  иск вращается с угловой скоростью, зависимость от времени которой задается графиком. иск вращается с угловой скоростью, зависимость от времени которой задается графиком. Найти угол поворота диска (в радианах) за 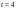 с, если с, если 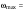 2 с–1. 2 с–1.Угол поворота диска за малый промежуток времени 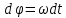 Подставим сюда зависимость угловой скорости от ускорения Подставим сюда зависимость угловой скорости от ускорения 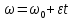 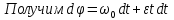 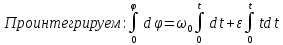 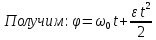 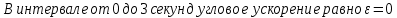 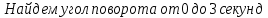 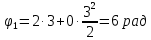 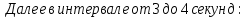 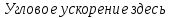 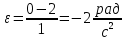 Угол поворота от 3 до 4 секунд 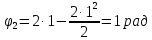 Суммарный угол поворота равен Суммарный угол поворота равен 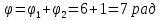 9.3. Частица движется в плоскости так, что ее импульс зависит от времени по закону 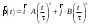 , где , где 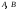 – постоянные величины, – постоянные величины, 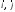 – единичные орты в декартовой системе координат. Найти тангенс угла между осью х и вектором силы, действующей на частицу в момент времени – единичные орты в декартовой системе координат. Найти тангенс угла между осью х и вектором силы, действующей на частицу в момент времени 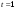 с, если с, если 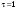 с. с.А = 2 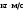 , В = 3 , В = 3 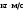 . а) 6,25; б) 5,25; в) 4,25; г) 3,25; д) 2,25; . а) 6,25; б) 5,25; в) 4,25; г) 3,25; д) 2,25;Решение За вторым законом Ньютона в импульсной форме 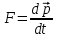 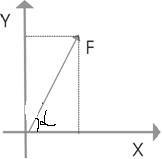 Продифференцируем выражение для импульса по времени 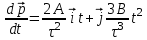 Искомый угол равен отношению игрековой проекции силы к иксовой 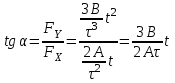 Подставим числа 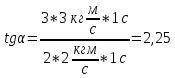 9.4. Маленький шарик поместили в точку с радиусом-вектором 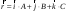 . В некоторый момент на шарик подействовали силой . В некоторый момент на шарик подействовали силой 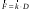 . Найти модуль момента силы относительно начала отсчета. А, В, С и D – некоторые постоянные; . Найти модуль момента силы относительно начала отсчета. А, В, С и D – некоторые постоянные; 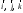 – единичные орты в декартовой системе координат. A= 2 м, В = 3 м, С = 4 м, D = 5 Н. – единичные орты в декартовой системе координат. A= 2 м, В = 3 м, С = 4 м, D = 5 Н.а) 22 Нм; б) 20 Нм; в) 18 Нм; г) 16 Нм; д) 14 Нм; дано A= 2 м, В = 3 м С = 4 м D = 5 Н. М-? Решение: Момент силы в данном случае равен 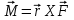 Векторное произведение двух векторов 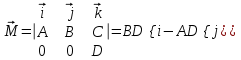 Модуль этого вектора 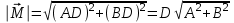 вычислим 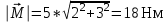 Правильный ответ: в) 18 Нм; 9.6 Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 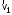 . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью 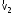 и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите величину импульса шариков после удара. и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите величину импульса шариков после удара. 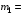 3 кг, 3 кг, 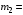 4 кг, 4 кг, 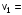 5 м/с, 5 м/с, 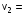 6 м/с. 6 м/с. а) 26,3 кгм/с; б) 28,3 кгм/с; в) 30,3 кгм/с; г) 32,3 кгм/с; д) 34,3 кгм/с; Д 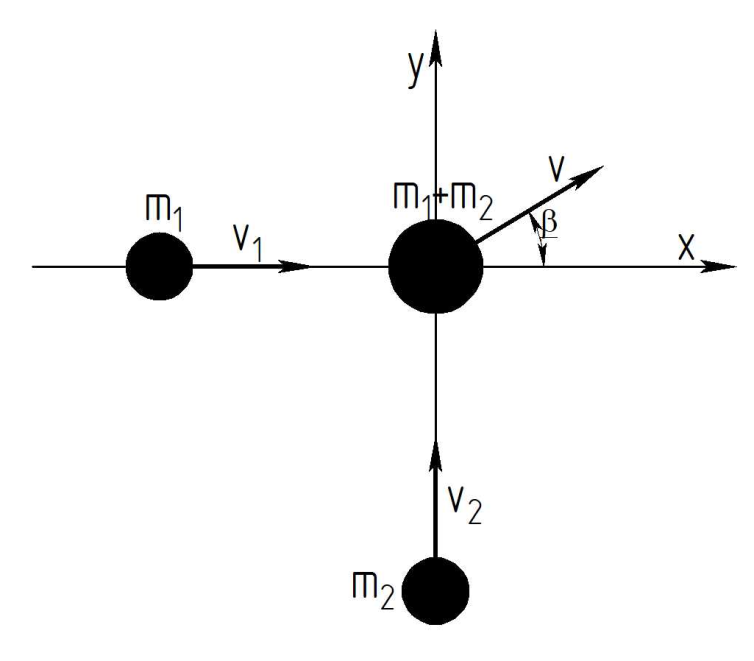 ано: ано: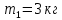 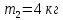 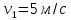 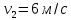 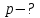 По закону сохранения импульса в проекции на ось х 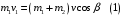 Запишем закон сохранения импульса в проекции на ось y 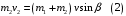 Разделим (2) на (1): 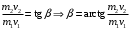 Импульс шариков после удара 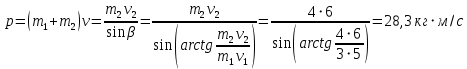 9.6. Н  а горизонтальной плоскости лежит тонкий однородный стержень массы m и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью а горизонтальной плоскости лежит тонкий однородный стержень массы m и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью а) 0,85 м; б) 0,75 м; в) 0,65 м; г) 0,55 м; д) 0,45 м; дано 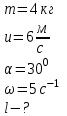 решение используем для решения закон сохранения момента импульса 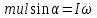 подставим сюда суммарный момент импульса стержня и шарика 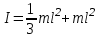 имеем 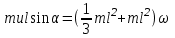 отсюда длина стержня 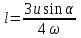 вычислим 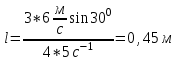 9  .7 .7Тонкий однородный стержень массы m и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите скорость центра масс стержня в момент прохождения им положения равновесия. Сопротивлением воздуха пренебречь. m = 2 кг, l= 3 м, g = 10 м/с2. а) 1,74 м/с; б) 2,74 м/с; в) 3,74 м/с; г) 4,74 м/с; д) 5,74 м/с; Дано: 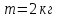 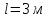 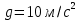 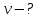 По закону сохранения энергии 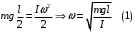 Момент инерции стержня 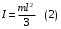 Угловая и линейная скорости связаны соотношением 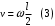 Подставим (1) в (3) с учетом (2), получим: 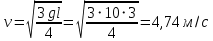 9.8 Тонкий однородный диск массы mи радиуса Rподвешен на горизонтальной оси, проходящей перпендикулярно диску через его край О.К диаметрально противоположному краю диска прикрепили небольшой пластилиновый шарик такой же массы m. Найдите частоту малых колебаний такого маятника. Трением в оси пренебречь. Принять g = 10 м/с2. m = 2 кг, R= 2 м. а) 6,8 с; б) 5,8 с; в) 4,8 с; г) 3,8 с; д) 2,8 с; Д  ано: ано: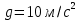 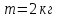 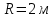 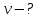 Период колебаний 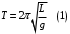 Приведенная длина 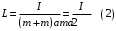 Расстояние от центра масс до оси колебаний 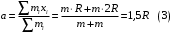 Момент инерции 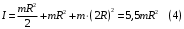 Подставим (2) в (1) с учетом (3) и (4), получим: 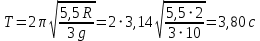 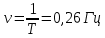 9.9. В воздушном шарике находится одноатомный идеальный газ. Газ расширяется от объема V1 до объема V2, при этом его давление меняется по закону 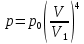 . Найти работу, совершенную газом в этом процессе. p0= 2105 Па; V1= 1 м3; V2=2 м3. . Найти работу, совершенную газом в этом процессе. p0= 2105 Па; V1= 1 м3; V2=2 м3.а) 4,24 МДж; б) 3,24 МДж; в) 2,24 МДж; г) 1,24 МДж; д) 0,24 МДж; Дано: 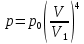 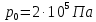 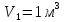 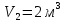 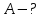 Работа 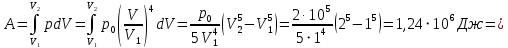 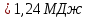 9.10. П 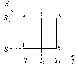 ервая тепловая машина совершает циклический процесс ервая тепловая машина совершает циклический процесс 1–4–3–2–1, а вторая 4–6–5–3–4 (см. график). На сколько процентов больше коэффициент полезного действия первой тепловой машины. T1 = 400 К; T2 = 600 К; Т3 = 800 К. S1 = 1 Дж/К; S2 = 5 Дж/К. а) 6,33%; б) 8,33%; в) 10,3%; г) 12,3%; д) 14,3%; Дано: 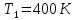 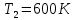 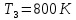 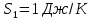 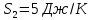 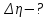 Коэффициент полезного действия 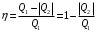 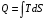 На участках где S увеличивается, тепло поступает, где S уменьшается, тепло отдается. Если S=const, то Q=0 Количество теплоты 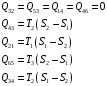 Для первой тепловой машины Количество теплоты подводимое к системе 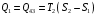 Количество теплоты отводимое от системы 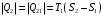 Для второй тепловой машины Количество теплоты подводимое к системе 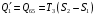 Количество теплоты отводимое от системы 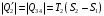 Тогда 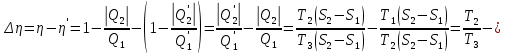 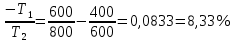 |
