7 вариант. Решение задач 7 вариант Задача 23
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
|
Физика решение задач 7 вариант Задача 1.23 Кинетические уравнения движения двух материальных точек имеют вид x1 = A1t + B1t2 + C1t3 и x2 = A2t + B2t2 + C2t3, где B1 = 4 м/с2, C1 = – 3 м/с3, B2 = -2 м/с2 C2 = 1 м/c3. Определите момент времени, для которого ускорения этих точек будут равны. Решение: Найдем законы изменения скорости материальных точек: 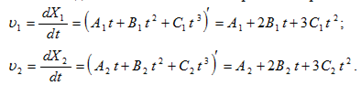 Найдем законы изменения ускорения материальных точек: 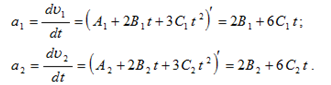 Найдем момент времени t, в который ускорения точек будут равны: 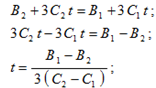 Находим t: 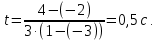 Ответ: t=0,5 с. Задача 1.73 Определите координаты центра масс системы, состоящей из четырех шаров массами 2m, 3m, 4m и m, которые расположены в вершинах и в центре равностороннего треугольника со стороной a = 20 см. Направление координатных осей показано на рисунке. 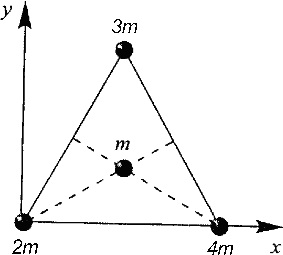 Решение: 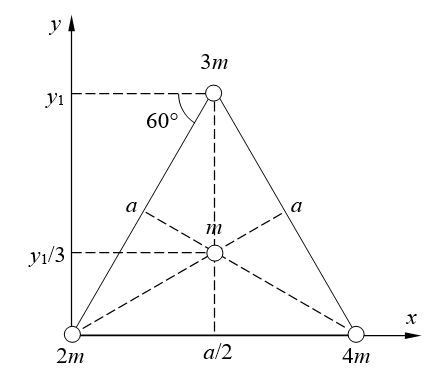 Из рисунка: 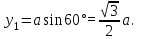 Координаты центра масс системы: 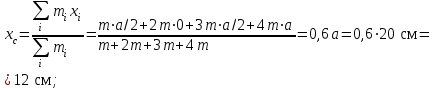 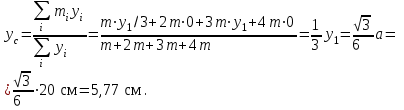 Ответ: хс = 12 см, ус = 5,77 см Задача 1.128 Шар сталкивается с другим покоящимся шаром такой же массы. Докажите, что в случае упругого, но не центрального удара угол между направлениями скоростей после удара составляет π/2. Решение: Пусть Закон сохранения импульса: Закон сохранения энергии: Сокращая массы и умножая первое уравнение скалярно само на себя, получаем: Сравнивая первое и второе уравнения, заключаем, что Ответ: 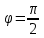 . .Задача 1.199 Два спутника с одинаковой массой движутся вокруг Земли по круговым орбитам разных радиусов R1 и R2 (R2>R1). Определите: 1) отношение кинетической энергии второго спутника к первому, 2) как зависят от радиуса орбиты потенциальная и полная энергия спутников. Решение:  Задача 1.247 Объясните, зависит ли разность давлений на нижнюю и верхнюю поверхность крыла самолета от высоты его подъема. Решение: Возникновение подъемной силы крыла самолета тоже является следствием уравнения Бернулли. При обтекании крыла самолета набегающим потоком воздуха на задней кромке крыла образуется завихрение, в котором воздух вращается против часовой стрелки (если крыло движется справа налево). По закону сохранения момента импульса должен возникнуть круговой поток по часовой стрелке. Такое движение воздуха возникает вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом. Но согласно уравнению Бернулли, там, где скорость больше, давление меньше. Значит давление воздуха на нижнюю часть крыла самолета больше, чем на верхнюю. Эта разность давлений и создает подъемную силу. Заметим еще, что на уравнении Бернулли основано действие многих технических устройств и, в частности, работа пульверизатора и карбюратора. Ответ: 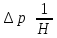 . .Задача 2.9 В сосуде вместимостью 5 л при нормальных условиях находится азот. Определите: 1) количество вещества ν; 2) массу азота; 3) концентрацию n его молекул в сосуде. Решение: Так как азот находится при нормальных условиях, то его давление и температура равны: Уравнение Менделева-Клайперона: Откуда 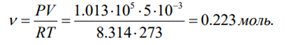 Масса азота: Концентрация молекул в сосуде: 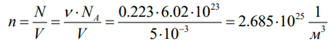 Ответ:1). v=0,223 моль, 2). m=6,24 г, 3). N=2,685·1025 1/м3. Задача 2.82 Идеальный газ (ν = 2 моль) сначала изобарно нагрели, так что объем газа увеличился в n = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n = 2 раза. Определите приращение энтропии в ходе указанных процессов. Решение: Изохорный процесс: 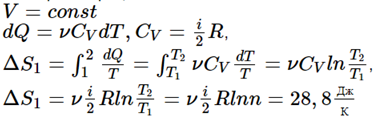 Изобарный процесс: 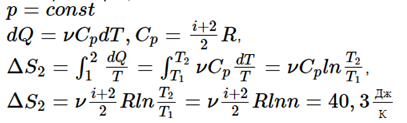 Приращение энергии: 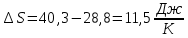 Ответ: 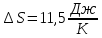 . .Задача 3.33 Электростатическое поле создается бесконечной прямой нитью, заряженной равномерно с линейной плотностью τ = 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии r = 0,5 м от нити. Решение: Бесконечная, равномерно заряженная нить, создает аксиально симметричное поле с напряженностью E=τ2πεε0r Напряженность и потенциал связаны выражением E=-dφdt Откуда dφ=-E∙dr Тогда получаем gradφ=Egradφ=τ2πεε0rgradφ=(50∙10-10)2∙3,14∙8,85∙10-12∙0,5=179,9 Bм Градиент направлен к нити. Ответ: grad φ=179,9 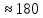 Bм, градиент направлен к нити. Bм, градиент направлен к нити. Ответ: grad φ=180 Bм, градиент направлен к нити. Задача 3.116 В однородном магнитном поле с индукцией B = 1 Тл находится квадратная рамка со стороной а = 10 см, по которой течет ток I = 4 А. Плоскость рамки перпендикулярна линиям магнитной индукции. Определите работу А, которую необходимо затратить для поворота рамки относи оси, проходящей через середину ее противоположных сторон: 1) на 90°; 2) на 180°; 3) на 360°. Решение: Момент силы: 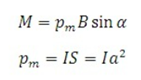 Работа: 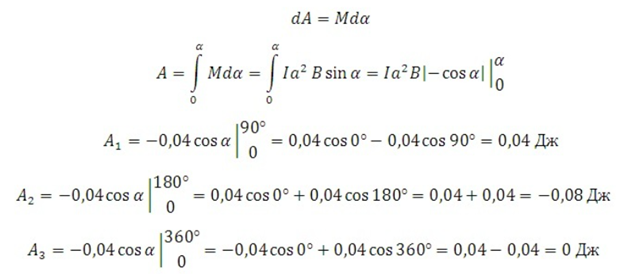 Ответ: 1). A1=0,04 Дж, 2). A2=0,08 Дж, 3). A3=0. Задача 3.205 Две катушки намотаны на один сердечник. Индуктивность первой катушки L1 = 0,12 Гн, второй — L2 = 3 Гн. Сопротивление второй катушки R2 = 300 Ом. Определите силу тока I2 во второй катушке, если за время ∆t = 0,01 с силу тока в первой катушке уменьшить от I1 = 0.5 А до нуля. Решение: Если в катушке 1 течет ток I1, то магнитный поток, создаваемый этим током пропорцианален I1. Обозначим через Ф21 ту часть потока, которая пронизывает контур 2. Тогда где L21 – коэффициент взаимной индукции. Если ток I1 изменяется, то в катушке 2 индуцируется ЭДС По закону Ома 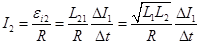 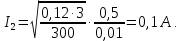 Ответ: I2=0,1 А. Задача 4.29 Тонкий обруч радиусом R = 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определите период T колебаний обруча. Решение: 1). Момент инерции обруча относительно центра: J₀ = m·R² 2). Чтобы определить момент инерции обруча, считая центром вбитый гвоздь, воспользуемся теоремой Штейнера: J = J₀ + m·R² = m·R² + m·R² = 2·m·R² 3). Рассматривая обруч как физический маятник, находим его период: T = 2π·√(J/(R·m·g) ) = 2π·√(2·m·R²/(R·m·g)) = = 2π·√(2·R/g) T = 2·3,14·√(2·0,5/10) ≈ 2 с Ответ: T=2 с. Задача 4.89 Гиря массой m = 200 г, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,2 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,2 cos ωt, Н. Определите: 1) частоту ν0 собственных колебаний; 2) резонансную частоту νрез; 3) резонансную амплитуду Aрез; 4) статическое отклонение. Решение: 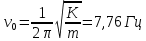 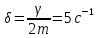 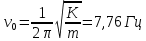 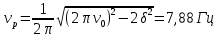 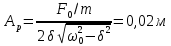 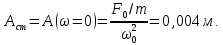 Ответ: 1). 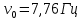 , 2). , 2).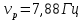 , 3). , 3). 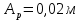 , 4). , 4). 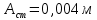 Задача 4.146 Определите, на сколько фонов увеличился уровень громкости звука, если интенсивность звука увеличилась: 1) в 1000 раз; 2) в 10 000 раз. Решение:  Ответ: 1). На 30 фон; 2). На 40 фон. Задача 5.22 На рисунке показаны положения главной оптической оси MN тонкой линзы, светящейся точки S и ее изображения S'. Определите построением оптический центр линзы и ее фокусы. Укажите вид линзы. Среды по обе стороны линзы одинаковы.  Задача 5.74 На зонную пластинку падает плоская монохроматическая волна (λ = 0,5 мкм). Определите радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения b = 1 м. Решение: rk = √ (k·b·λ) r₁ = √ (1·1·0,5·10⁻⁶) = 707·10⁻⁶ м = 707 мкм Ответ: r1=707 мкм. Задача 5.136 Определите минимальную кинетическую энергию, которой должен обладать электрон, чтобы в среде с показателем преломления n = 1,5 возникло черенковское излучение. Ответ выразите в МэВ. Решение: Эффект Вавилова — Черенкова 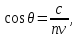 где θ — угол между направлением распространения излучения и вектором скорости частицы; c— скорость света в вакууме;n — показатель преломления среды; v — скорость частицы. Отсюда 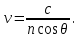 Минимальную скорость получим при максимальном значении функции косинус, которое равно 1 при θ = 0: 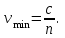 При этом кинетическая энергия релятивистского электрона равна 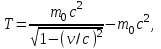 где m0 — масса покоя частицы. 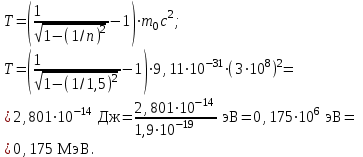 Ответ: T = 0,175 МэВ. Задача 5.183 Металлическая поверхность площадью S = 15 см2, нагретая до температуры T = 3 кК, излучает в одну минуту 100 кДж. Определите: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверхности и черного тела при данной температуре. Решение: Энергия, излучаемая поверхностью за единицу времени: 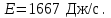 Энергия, которую излучало бы абсолютно черное тело за единицу времени: 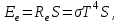 где 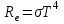 ― закон Стефана-Больцмана. ― закон Стефана-Больцмана.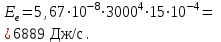 Отношение энергетических светимостей этой поверхности и черного тела при температуре T: 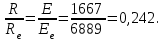 Ответ: Ee = 6889 Дж/с; R/Re = 0,242. Задача 5.235 Фотон с энергией ε = 0,25 МэВ рассеялся под углом ν = 120° на первоначально покоившемся электроне. Определите кинетическую энергию электрона отдачи. Решение: 1. Энергию рассеянного фотона εнайдем, воспользовавшись формулой Комптона: 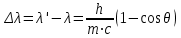 , ,Выразив длины волн 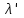 рассеянного и рассеянного и 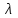 падающего фотонов через энергии падающего фотонов через энергии 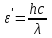 и и 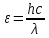 соответствующих фотонов: соответствующих фотонов: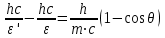 Разделим обе части этого равенства на hc: 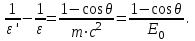 Отсюда, обозначив для краткости энергию покоя электрона 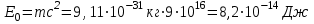 , найдем энергию рассеянного фотона: , найдем энергию рассеянного фотона: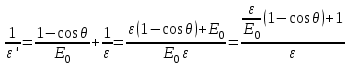 Следовательно, энергия рассеянного фотона: 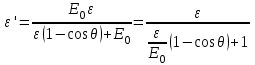 (1) (1)Подставив числовые значения величин, получим: 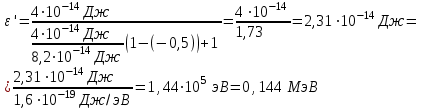 2. Кинетическая энергия электрона отдачи Т, как это следует из закона сохранения энергии: 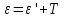 равна разности между энергией 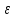 падающего фотона и энергией εрассеянного фотона: падающего фотона и энергией εрассеянного фотона: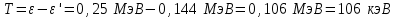 Ответ: 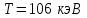 Задача 6.59 Докажите, что групповая скорость волн де Бройля равна скорости свободно движущейся частицы. Рассмотрите нерелятивистский и релятивистский случаи. Решение: Рассмотрим свободно движущуюся со скоростью v частицу массой т. Вычислим для нее фазовую и групповую скорости волн де Бройля. Фазовая скорость, согласно (154.8), 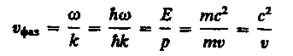 (214.1) (214.1)(E = ℏw и p = ℏk, где k = 2p/ l — волновое число). Так как c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме (фазовая скорость волн может быть как меньше, так и больше с в отличие от групповой скорости волн (см. § 155)). Групповая скорость, согласно (155.1),  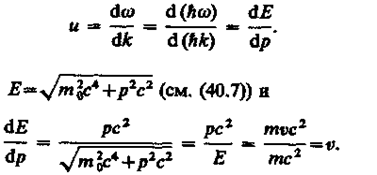 Следовательно, групповая скорость волн де Бройля равна скорости частицы. Групповая скорость фотона т. е. равна скорости самого фотона. Волны де Бройля испытывают дисперсию (см. § 154). Действительно, подставив в выражение (214.1) vфаз = E/pформулу (40.7) Задача 6.102 Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 3). Определите, в каких точках "ямы" (0 <= х <= l) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните полученный результат графически. Решение: Вероятность обнаружить частицу в интервале от x до x+dx 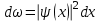 где волновая функция 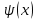 частицы в потенциальной яме шириной l на n-ом энергетическом уровне имеем вид: частицы в потенциальной яме шириной l на n-ом энергетическом уровне имеем вид: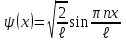 Для основного состояния n=1. Плотность вероятности 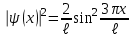 Для того чтобы найти экстремумы (минимумы и максимумы) необходимо производную 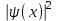 по x приравнять к нулю по x приравнять к нулю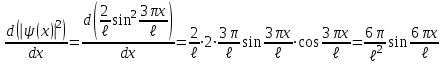 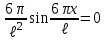 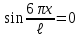 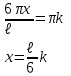 Плотность вероятности в точках интервала 0<х<l, при k=0,1,2… При 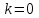 , x=0 , , x=0 , 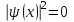 При 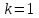 , , 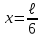 , , 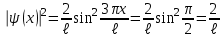 При 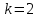 , , 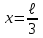 , , 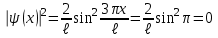 При 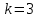 , , 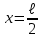 , , 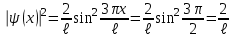 При 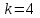 , , 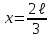 , , 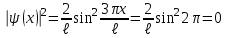 При 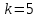 , , 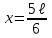 , , 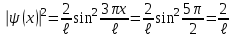 При 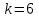 , , 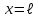 , , 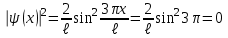 Плотность вероятности обнаружения частицы минимально в точках 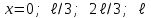 Плотность вероятности обнаружения частицы максимально в точке 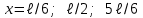 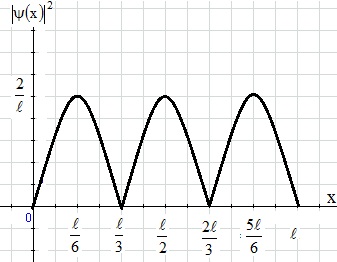 Ответ: минимум в точках 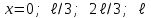 , максимум в точке , максимум в точке 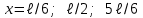 Задача 6. 146 Объясните, почему в опыте Штерна и Герлаха по обнаружению собственного механического момента импульса (спина) электрона использовался пучок атомов водорода, заведомо находящихся в 1s-состоянии. Решение:  Задача 6.173 Объясните механизм возникновения, свойства и особенности вынужденного (индуцированного) излучения. Решение:  Задача 6.195 Объясните образование зонного эффекта энергетического спектра в кристалле, показав, что этот эффект – квантово-механический и вытекает из соотношения неопределенности Гейзенберга. Решение:  Задача 6.216 Чем объясняется при контакте двух металлов: 1) возникновение внешней контактной разности потенциалов? 2) возникновение внутренней контактной разности потенциалов. 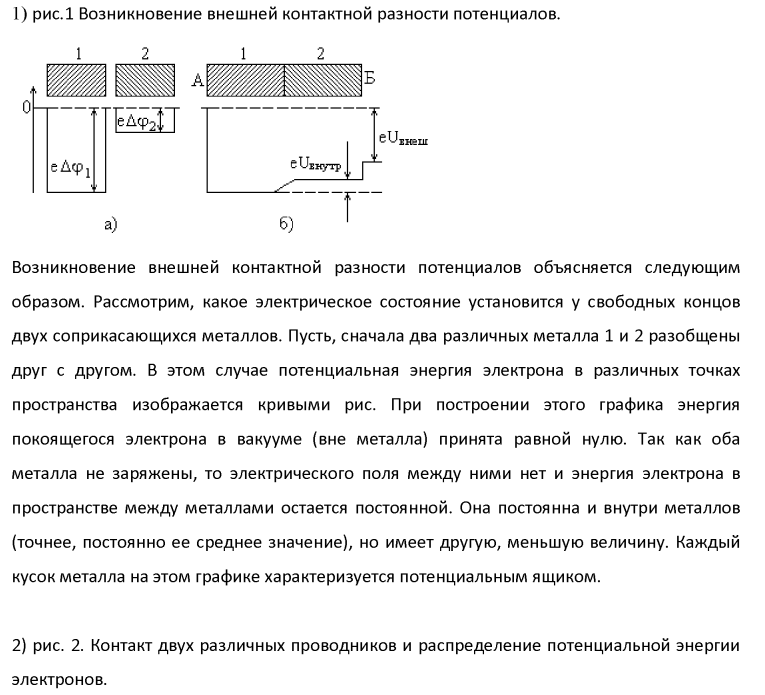   Задача 7.19 Определите число нуклонов, которые могут находиться в ядре на низшем квантовом уровне. Решение. По сложившейся в европейской физике традиции, ядерная конфигурация с данными квантовыми числами n и ℓ обозначается как (n+1)ℓj, причем вместо цифровых значений ℓ используются буквеннные (s, p, d, f, g, h, i …). Низшему состоянию нуклона соответствует конфигурация 1s. В этом энергетическом состоянии может находиться не более 4 нуклонов ― 2 протона с противоположными значениями проекции спина на ось и 2 нейтрона в таких же состояниях. Ответ: N=4. Задача 7.54 Запишите превращение нейтрона в протон с указанием частиц, которые при этом испускаются. Объясните, почему этот процесс является энергетически возможным.  Задача 7.79 Задача 7.79Для обнаружения нейтрона используются реакции захвата тепловых нейтронов легкими ядрами ( 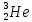 , , 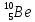 ), в результате которых испускаются заряженные частицы. Запишите возможные реакции. ), в результате которых испускаются заряженные частицы. Запишите возможные реакции.Ответ: Под действием медленных нейтронов на некоторых легких ядрах наблюдаются также реакции захвата нейтронов с испусканием заряженных частиц – протонов и альфа-частиц (под действием тепловых нейтронов): Задача 7.104 Известно, что продукты распада заряженных пионов испытывают дальнейший распад. Запишите цепочку реакций для 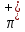 – и – и 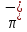 –. –.Ответ:   |
