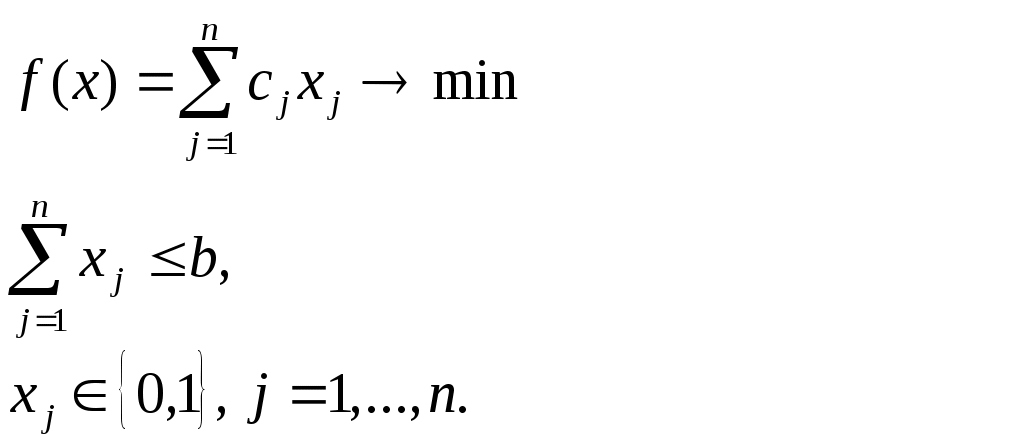Лабораторная работа 3. Решение задачи о рюкзаке приближенными и точными алгоритмами.
Задача о рюкзаке и ее варианты широко используются для моделирования большого числа практических задач управления, таких как выбор проектов, распределение капитала, комбинаторные аукционы, расположение предметов в системах сборки по заказу и др. [3, 6, 7].
Одним из частных случаев задачи о рюкзаке является одномерная булева задача о рюкзаке, которая может быть сформулирована следующим образом. Рассмотрим рюкзак с объемом равным b. Пусть существует n различных предметов. Предмет j занимает объем aj, при этом его ценность равна cj. Цель задачи состоит в максимизации выгоды от помещенных в рюкзак предметов. Таким образом, задача может быть сформулирована как задача булева линейного программирования в следующем виде:
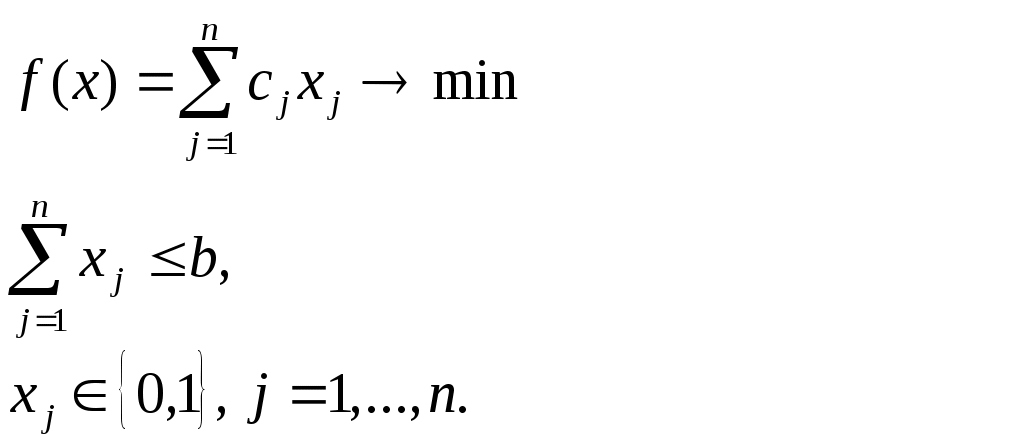
Если условие 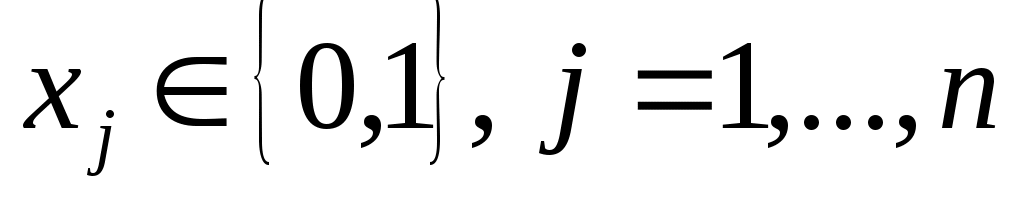 заменить условием заменить условием 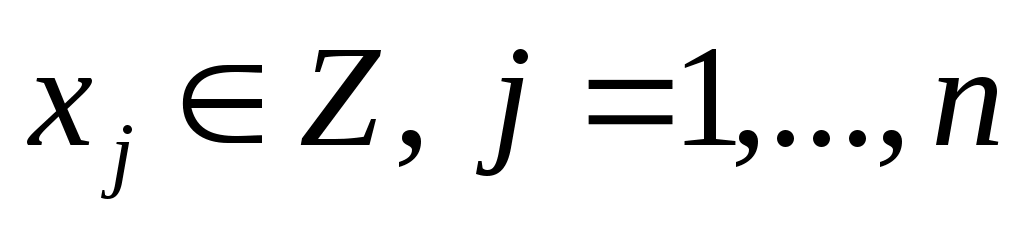 , то получим задачу об одномерном целочисленном рюкзаке. В этом случае имеется nтипов предметов и требуется определить, сколько предметов каждого типа нужно поместить в рюкзак, чтобы они имели максимальную суммарную ценность. , то получим задачу об одномерном целочисленном рюкзаке. В этом случае имеется nтипов предметов и требуется определить, сколько предметов каждого типа нужно поместить в рюкзак, чтобы они имели максимальную суммарную ценность.
Для решения задачи о рюкзаке разработан целый ряд алгоритмов и методов: динамическое программирование [6], метод ветвей и границ [3], метод перебора L-классов [2] и другие.
В случае небольших n одномерная задача о рюкзаке может быть также решена в табличном процессоре MS Excel. При этом исходные данные задачи записываются также, как и для задачи ЛП, но в окне Поиск решения, Ограничения необходимо указать, что переменные являются целыми, либо булевыми (рис. 10).
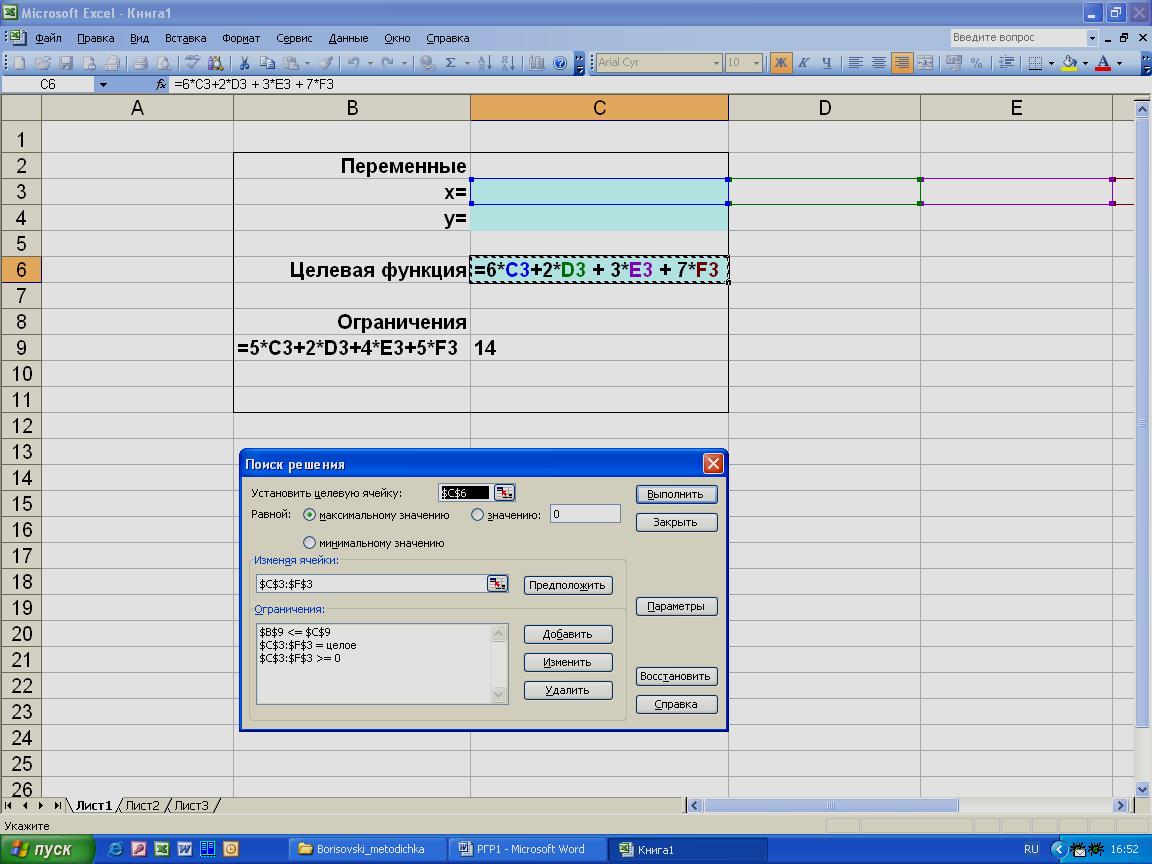
Рис. 10. Диалоговое окно Поиск решения для задачи о рюкзаке.
При больших n точное решение задачи может потребовать значительных затрат машинного времени. Поэтому актуальной является разработка приближенных алгоритмов. Самый известный приближенный алгоритм – это так называемый “жадный” алгоритм. Опишем этот алгоритм по шагам для булевого случая.
«Жадный» алгоритм.
Шаг 1. Упорядочить предметы по не возрастанию удельной полезности cj/ aj,
т.е. так, чтобы выполнялось соотношение
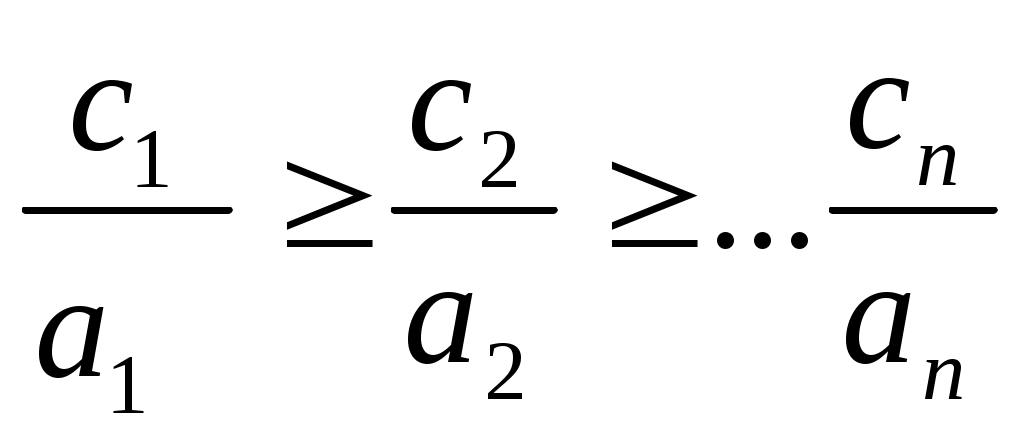 , ,
положить k:=1 и перейти на шаг 2.
Шаг 2. Если ak≤ b, то положить xk:=1, b:=b – ak, иначе xk:= 0.
Увеличить k на единицу и перейти на шаг 3.
Шаг 3. Если k > n, то алгоритм завершает работу, иначе перейти на шаг 2.
Варианты заданий. Решить задачу о рюкзаке в пакете MS Excel. Разработать алгоритм полного перебора и «жадный» алгоритм для задачи о рюкзаке [8]. Найти точное и приближенное решение задачи о рюкзаке, используя реализованные алгоритмы.
1) 6x1+ 2x2+ 3x3+ 7x4 → max
5x1+ 2x2+ 4x3+ 5x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
2) 2x1+ 4x2+ 4x3+ 3x4 → max
2x1+5x2+ 3x3+4x4 ≤ 12
xi ≥ 0, xiє Z, i = 1,..,4.
|
3) 3x1+ 6x2+ 5x3+ x4 → max
2x1+ 5x2+4x3+ x4 ≤ 15
xi ≥ 0, xiє Z, i = 1,..,4.
|
4) 2x1+ 2x2+ x3+3x4 → max
2x1+ 3x2+ 2x3+ 3x4 ≤ 13
xi ≥ 0, xiє Z, i = 1,..,4.
|
5) 5x1+ x2+ x3+ 3x4 → max
4x1+ 3x2+ x3 + 3x4 ≤ 13
xi ≥ 0, xiє Z, i = 1,..,4.
|
6) x1+ 5x2+ 2x3+ 3x4 → max
2x1+ 4x2+ 5x3+ 3x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
7) 5x1+ 7x2+ 6x3+ 3x4 → max
4x1+ 5x2+ 8x3+ 3x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
8) x1+ 7x2+ 3x3+ 4x4 → max
x1+ 5x2+ 2x3+ 3x4 ≤ 13
xi ≥ 0, xiє Z, i = 1,..,4.
|
9) x1+ 7x2+ 7x3+ 4x4 → max
2x1+ 6x2+ 4x3+ 3x4 ≤ 15
xi ≥ 0, xiє Z, i = 1,..,4.
|
10) 3x1+ 5x2+ 2x3+ 8x4 → max
2x1+ 4x2+ x3+ 6x4 ≤ 15
xi ≥ 0, xiє Z, i = 1,..,4.
|
11) x1+ 5x2+ 6x3+ 3x4 → max
2x1+ 4x2+ 5x3 + 3x4 ≤ 15
xi ≥ 0, xiє Z, i = 1,..,4.
|
12) 4x1+ 5x2+ 2x3+4x4 → max
2x1+2x2+ x3+ 3x4 ≤ 13
xi ≥ 0, xiє Z, i = 1,..,4.
|
13) 3x1+ 7x2+ 7x3+ 5x4 → max
4x1+ 7x2+ 5x3+ 6x4 ≤ 13
xi ≥ 0, xiє Z, i = 1,..,4.
|
14) 2x1+ 4x2+ 5x3+ 6x4 → max
2x1+ 3x2+ 4x3+ 5x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
15) 5x1+ 6x2+ 3x3+ 4x4 → max
4x1+ 7x2+ 3x3+ 5x4 ≤ 18
xi ≥ 0, xiє Z, i = 1,..,4.
|
16) 5x1+ 6x2+ 9x3+ 4x4 → max
4x1+ 5x2+ 8x3+ 3x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
17) x1+ 7x2+ 3x3+ 8x4 → max
x1+ 4x2+ 2x3+ 5x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
18) 9x1+ x2+ 2x3+5x4 → max
8x1+ x2+3x3+4x4 ≤ 15
xi ≥ 0, xiє Z, i = 1,..,4.
|
19) 2x1+ 3x2+ 6 x3+9x4 → max
4x1+ 7x2+ 8x3+10x4 ≤ 20
xi ≥ 0, xiє Z, i = 1,..,4.
|
20) x1+ 8x2+ 9x3+7x4 → max
x1+ 5x2+ 8x3+ 6x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
21) 2x1+ 3x2+ 3x3+ 4x4 → max
4x1+ 4x2+ 5x3+ 5x4 ≤ 19
xi ≥ 0, xiє Z, i = 1,..,4.
|
22) 4x1+ 3x2+ 7x3+ x4 → max
4x1+ 5x2+ 8x3+ 2x4 ≤ 14
xi ≥ 0, xiє Z, i = 1,..,4.
|
23) x1+ 4x2+ 3x3+ 9x4 → max
x1+ 3x2+ 2x3+ 5x4 ≤ 17
xi ≥ 0, xiє Z, i = 1,..,4.
|
24) 7x1+ x2+ 3x3+2x4 → max
6x1+ x2+2x3+3x4 ≤ 20
xi ≥ 0, xiє Z, i = 1,..,4.
|
25) 2x1+ 3x2+ 6 x3+9x4 → max
4x1+ 7x2+ 8x3+10x4 ≤ 20
xi ≥ 0, xiє Z, i = 1,..,4.
|
26) x1+ 6x2+ 7x3+4x4 → max
x1+ 5x2+ 4x3+ 3x4 ≤ 19
xi ≥ 0, xiє Z, i = 1,..,4.
|
27) 2x1+ 5x2+ 3x3+ 7x4 → max
x1+ 3x2+ 2x3+ 5x4 ≤ 27
xi ≥ 0, xiє Z, i = 1,..,4.
|
28) 5x1+ x2+ 3x3+7x4 → max
4x1+ x2+2x3+3x4 ≤ 26
xi ≥ 0, xiє Z, i = 1,..,4.
|
29) 2x1+ 3x2+ 6 x3+7x4 → max
3x1+ 7x2+ 8x3+ 9x4 ≤ 25
xi ≥ 0, xiє Z, i = 1,..,4.
|
30) x1+ 6x2+ 4x3+4x4 → max
x1+ 5x2+ 4x3+ 3x4 ≤ 29
xi ≥ 0, xiє Z, i = 1,..,4.
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.