Коллоквиум. Коллоквиум 4. Задача о рюкзаке формулировка и решение
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
|
Построение i-го числа Фибоначчи Минусы рекурсивного построения: Одно и то же значение вычисляется много раз; использование памяти для стека рекурсивных вызовов; медленнее, чем итеративно 2. Мемоизация · Применение мемоизации в поиске i-го числа Фибоначчи 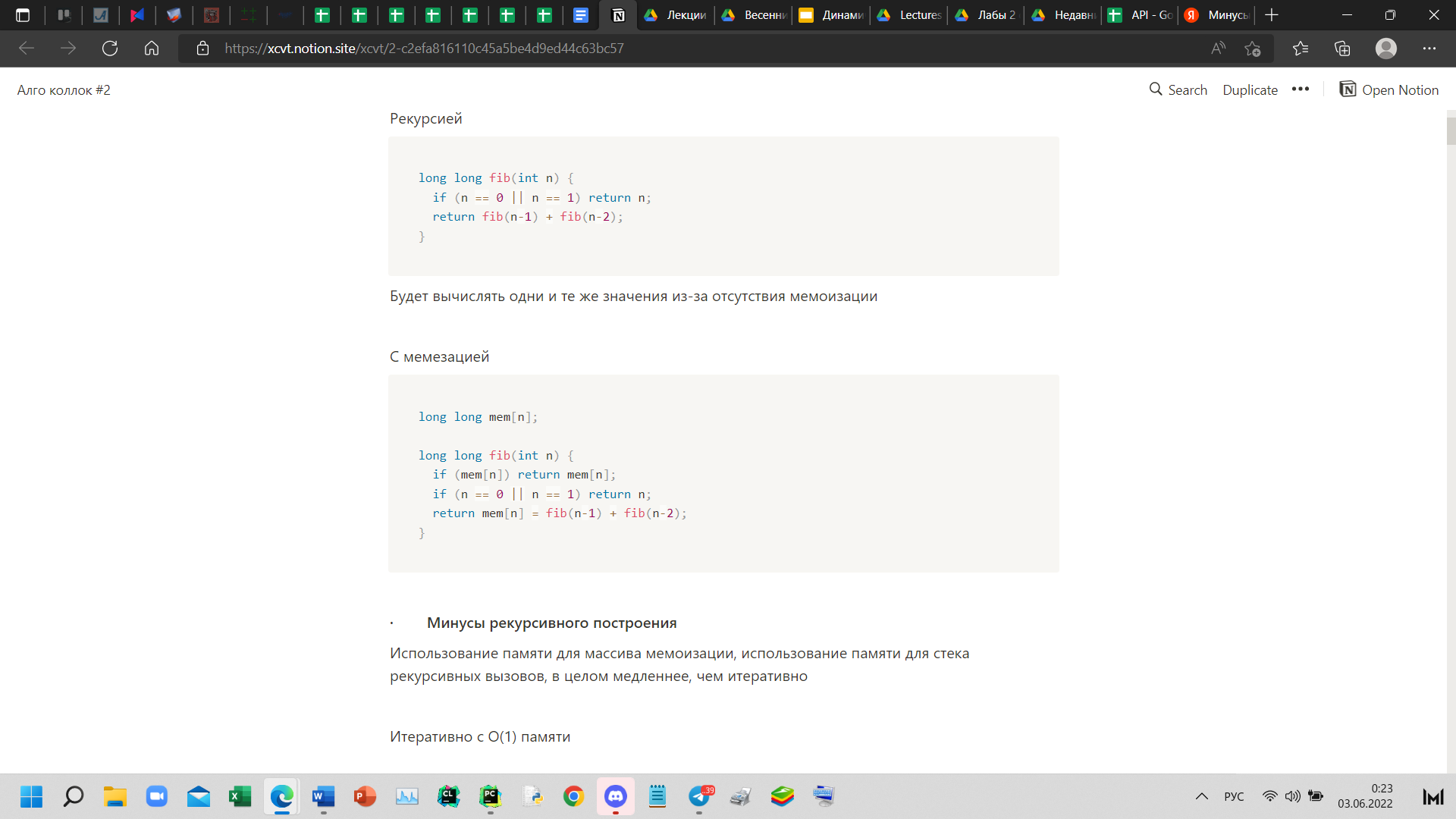 · Что такое мемоизация: Запоминание ранее вычисленных данных для избежания повторного вычисления · Плюсы и минусы применения мемоизации (память, скорость выполнения) +Существенно быстрее, т.к. данные не будут вычисляться повторно -Использует доп. память 3. Динамика вперед и динамика назад на примере поиска кратчайшего пути в ациклическом графе · Поиск пути при помощи топологической сортировки 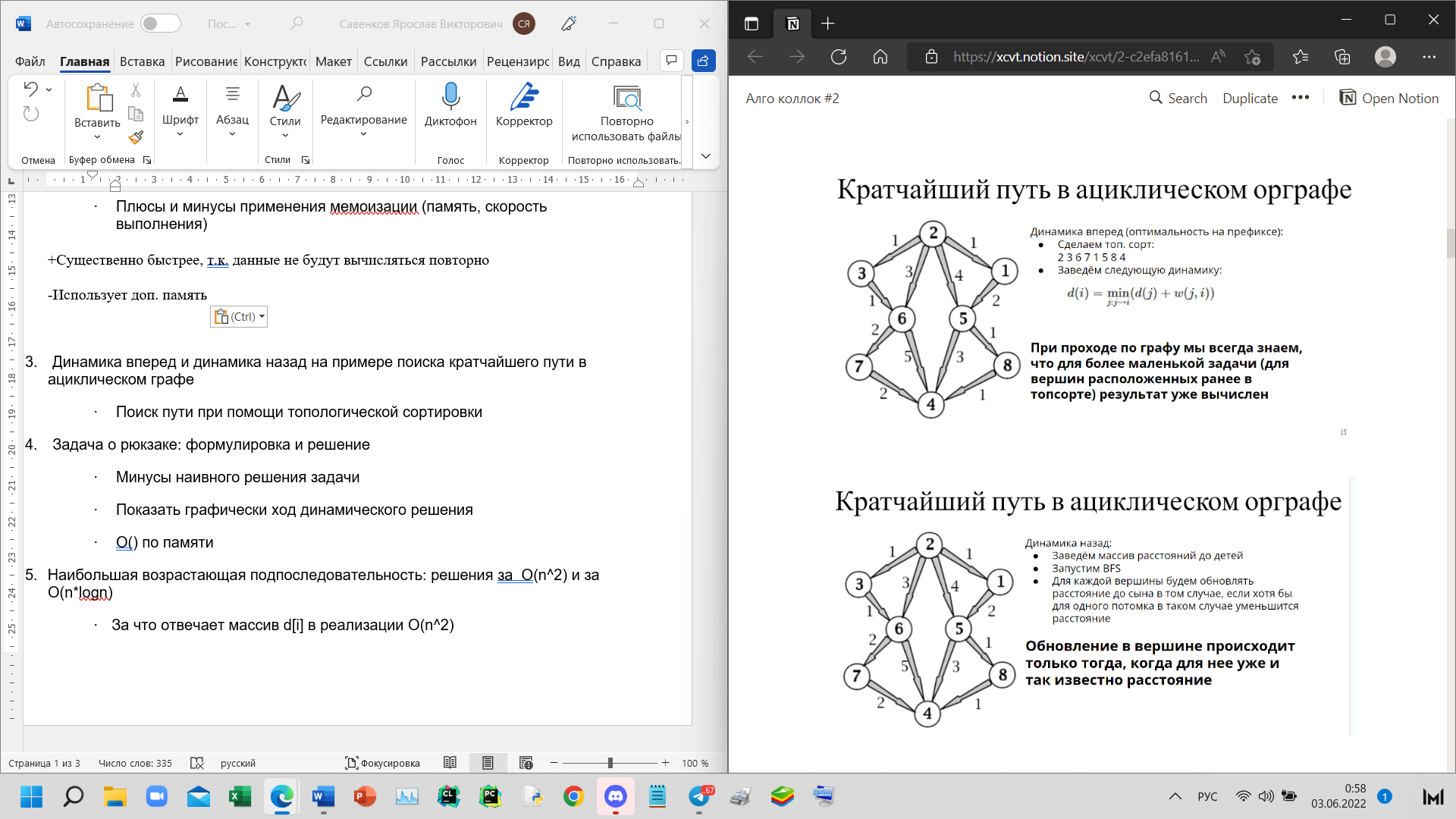  4. Задача о рюкзаке: формулировка и решение Дан рюкзак заданной вместимостью W Даны предметы у каждого его вес Wi и стоимость Ci Требуется наполнить рюкзак так, чтобы стоимость всех предметов в нем была максимальной · Минусы наивного решения задачи Для наивного решения мы могли бы перебрать всевозможные комбинации предметов таких будет 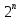 Либо некорректная идея - брать сначала предметы максимальной стоимостью, но этот жадный алгоритм сработает только если предмет можно поделить на части. · Показать графически ход динамического решения Ход решения - Имеем массив d[n][W] - обозначает максимальную стоимость рюкзака весом W до n-го предмета включительно  Заполним первую строку, взяв любой предмет, напишем его стоимость, если его вес ≤ второму текущему индексу i в d[0][i] Далее будем заполнять последовательно следующие строки, заполняя очередную клетку, мы либо возьмем клетку на одну строку выше, либо возьмем клетку d[s-1][i-w_i], то есть вычтем из текущей вместимости вес предмета и попытаемся вместе с ним взять предмет максимальной стоимости на оставшийся вес. · О(Wn) по памяти Проходимся по двумерному массиву размером W * n (макс. вместимость рюкзака и количество предметов) - тогда асимптотика O(Wn) 5. Наибольшая возрастающая подпоследовательность: решения за O(n^2) и за O(n*logn) · За что отвечает массив d[i] в реализации O(n^2) d[i] - максимальная длина подпоследовательности до i-го элемента · За что отвечает массив d[i] в реализации O(n*logn) число, на которое оканчивается подпоследовательность длины i · Разбор асимптотики O(n^2) Имеет внешний цикл n итераций, во внутреннем от 0 до i, то есть сумма прогрессии, то есть еще n, итого 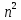 · Разбор асимптотики O(n*logn) Имеем внешний цикл n итераций, используем бинпоиск для вставки текущего элемента – log n, итого n*log n 6. Определения и постановка задачи о максимальном потоке · Каким условиям удовлетворяет поток Антисимметричность (если течет поток 5 в одном направлении, то -5 в другом) Ограничение потока (поток не может быть больше пропускной способности) Сохранение потока (вытекает только из источника, стекает только в сток, то есть сколько входит в вершину, столько должно и вытекать) · Что такое сеть Дана транспортная сеть - ориентированный взвешенный граф (V, E) с вершинами источника (s) и стока (t), веса ребер - пропускные способности (c) 7. Концепции: остаточная сеть, увеличивающие пути, разрезы · Минимальный разрез - это такой разрез, что сумма пропускных способностей ребер, пересекающих разрез, минимальна Минимальный разрез равен максимальному потоку · Разрез это Разрез - разбиение множества вершин сети на два непересекающихся множества S, T, при этом вершины истока/стока принадлежат соответствующим множествам. · Дополняющий путь это Дополняющий (увеличивающий) путь - простой путь из истока в сток в остаточной сети · Остаточная пропускная способность это Остаточная пропускная способность - величина потока, который можем дополнительно направить по ребру (u, v), не превысив пропускную способность c(u, v) ( 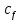 (u, v) = c(u,v) - f(u,v)) (u, v) = c(u,v) - f(u,v))8. Алгоритм Форда-Фалкерсона · Условие окончания работы алгоритма Не существует дополняющего пути (не можем дойти с вершины истока в сток по остаточной сети) · Показать графически ход алгоритма Изначально величина потока f(u,v) = 0 для всех ребер, а остаточная сеть равна исходной В остаточной сети дфсом находим любой путь из истока в сток. Если такого пути нет, алгоритм завершен Запоминаем минимальную остаточную пропускную способность min( 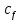 (u,v)) на пути, проходимся по пути и увеличиваем поток f(u,v) на мин. (u,v)) на пути, проходимся по пути и увеличиваем поток f(u,v) на мин. 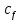 (u,v), уменьшаем поток в обратном направлении f(v,u) на мин. (u,v), уменьшаем поток в обратном направлении f(v,u) на мин. 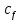 (u,v) (u,v)· Асимптотика На каждом шаге запускаем дфс и увеличиваем поток как минимум на единицу. f-максимальный поток в графе Следовательно имеем – O(E*f) 9. Поиск максимального паросочетания · Паросочетание это Паросочетание - множество несмежных ребер графа (никакие два ребра не имеют общей вершины) · Чередующая цепь это Чередующаяся цепь - путь в двудольном графе, для любых двух соседних рёбер которого верно, что одно из них принадлежит паросочетанию M, а другое нет. · Дополняющая цепь Дополняющая (увеличивающая) цепь - чередующийся путь, у которого начальная и конечная вершины свободные (не входят в паросочетание) 10. Лемма о перекрывающихся суффиксах · Если |x|<|y|, то x суффикс y · Если |x|>|y|, то y суффикс x · Если |x|=|y|, то x = y 11. Простейший алгоритм поиска подстрок · Асимптотика Внешний цикл - длина текста T (n), вложенный - длина образца S(m) O(nm) - в худшем O ( 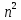 ), когда m = n ), когда m = n12. Итеративное вычисление полиномиальной хеш-функции, пересчет при сдвиге · Подсчет хеша  · Как меняется хеш-функция при сдвиге 13. Алгоритм Рабина-Карпа · Асимптотика · Асимптотика изменения значения хеш-функции  · Действия при одинаковых значениях хеш-функций При совпадении хэшей нужно сравнить строки посимвольно, т.к. возможны коллизии 14. Z-функция: тривиальный и эффективный алгоритмы · Асимптотика тривиального и эффективного алгоритмов Тривиальный: О( 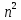 ) )Эффективный: О(n) · Графическое представление эффективного алгоритма  15. Построение префикс-функции · Асимптотика: О(n) · Графически показать построение  16. Построение конечного автомата · Роль префикс-функции в построении конечного автомата · Допускающее состояние · Графическое представление конечного автомата 17. Поиск подстрок с помощью конечных автоматов · Алгоритм поиска подстрок с помощью конечного автомата · Асимптотика |
