матем 20.11.. Решение задач на расположение прямых и плоскостей в пространстве (записать в тетради)
 Скачать 54.14 Kb.
|
|
Математика 20.11.2021 г. Задание: Повторить решение задач на расположение прямых и плоскостей в пространстве (записать в тетради). Заполнить сводную таблицу. Таблицу оформить на листе А4. Фото таблицы отправить на эл.адрес madeinborzya@yandex.ru до 24.11.2021 г. Дано: а и b - скрещивающиеся прямые; γ - плоскость, а ∉ γ, b ∈ γ. Точка M ∈ а, точка N ∈ b. Через а и N проведена плоскость α. Через b и М проведена плоскость β (рис. 1). Найти: а) лежит ли прямая b в плоскости α? б) пересекаются ли плоскости α и β? 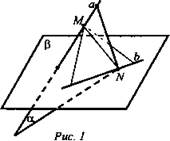 Решение: а) Если бы b ∈ α, тогда в плоскости α было бы две возможности: 1) b || а - но это противоречит условию; 2) b ∩ а - но это противоречит условию; b ∩ α в точке N, N ∉ а. Вывод: b ∉ α. б)  прямая MN - общая для плоскостей α и β.Ads by optAd360 Вывод: α ∩ β по прямой MN. (Ответ: b ∉ α, MN - прямая, по которой α ∩ β). 2. Дано: ABCD - параллелограмм; АВЕК - трапеция: ЕК - основание; ЕК ∉ (ABCD) (рис. 2). а) Выясните взаимное расположение прямых CD и ЕК. б) Найти: Р(ABEK), если АВ = 22,5 см; ЕК = 27,5 см. 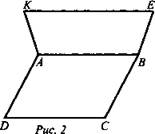 Решение: 1. CD || АВ - как противолежащие стороны параллелограмма АВ || ЕК - по определению трапеции. Значит, CD || ЕК. 2. Так как в трапецию можно вписать окружность, то АВ + КЕ = BE + АК. Тогда Р(ABEK) = (22,5 + 27,5) · 2 = 50 · 2 = 100 (см). (Ответ: a) CD || ЕК; б) Р(ABEK) = 100 см.) 3. Дано: ABCD - ромб; а || BD; А ∈ а; b ∈ (ABCD); с ∈ b (рис. 3). Доказать: a) a ∩ CD; б) а и b - скрещивающиеся прямые. 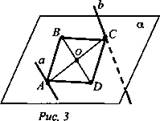 Ads by optAd360 Доказательство: А) 1. Прямая а проходит через точку А ∈ α, и а || BD (по условию), BD ∈ α, значит, а ∈ α. 2.  Б)  в точке D ⇒ (по теореме п. 7) а и b - скрещивающиеся прямые, что и требовалось доказать.Определение: Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости. 3. Дано: ABCD - пространственный четырехугольник; L - середина АВ; К - средина ВС; N - средина DC; М - средина DA (рис. 4). Доказать: LKNM - параллелограмм. 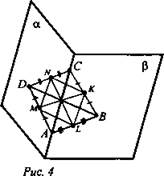 Решение: 1) LK - средняя линия ΔАВС,   2) MN - средняя линия ΔADC,   3) ML - средняя линия ΔADB,  Ads by optAd360 4) NK - средняя линия ΔCBD,  5)  6) Построим плоскость MNKL, которая по определению параллелограмма будет являться параллелограммом. Вывод: MNKL - параллелограмм. Сводная таблица по теме «Расположение прямых и плоскостей в пространстве»
|