курсовая. Решение задач по математике для студентов
 Скачать 447 Kb. Скачать 447 Kb.
|
|
Контрольные по математике. Решение задач по математике для студентов. № 1 Брошены две игральные кости, на каждой из которых могут выпасть цифры от 1 до 6. Найти вероятность того, что сумма выпавших на обеих костях очков равна 5, а произведение 4. Решение. Рассмотрим событие А – сумма выпавших на обеих костях очков равна 5. Вероятность события А вычислим с помощью классического определения вероятности где n – общее число равновозможных элементарных исходов испытания; m – число элементарных исходов, благоприятствующих появлению события A. Общее число различных случаев равно В сумме число 5 можно получить 4 способами: (1;4), (4;1), (2;3), (3;2) Тогда искомая вероятность равна Рассмотрим событие В – произведение выпавших на обеих костях очков равно 4. Вероятность события В вычислим с помощью классического определения вероятности . Общее число различных случаев равно Произведение очков, равное 4 можно получить 3 способами:(1;4), (4;1), (2,2). Тогда искомая вероятность равна Ответ: № 11 Даны независимые случайные величины X и Y. Найти математическое ожидание произведения
Решение. Так как X и Y – независимые величины, то мы имеем Математические ожидания величин X и Y найдем по формулам Тогда Дисперсию D(X) найдем по формуле Тогда Среднее квадратическое отклонение Ответ: №21 Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х); 3) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ( 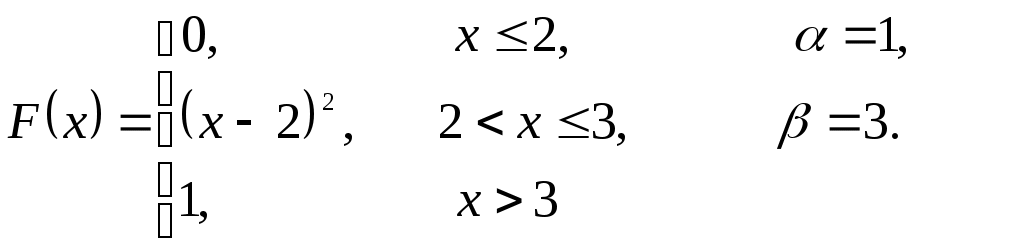 Решение. 1) Плотность распределения вероятностей f(x) будем искать как производную от функции распределения 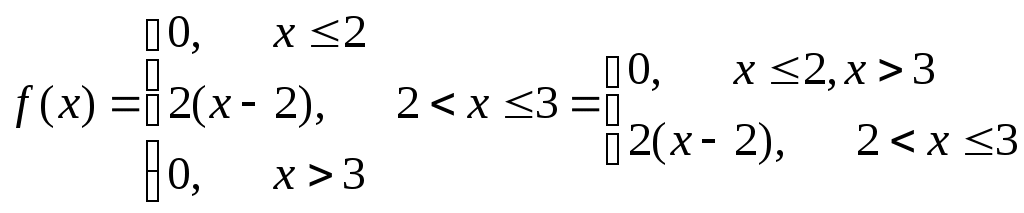 2) Построим график функции f(x) 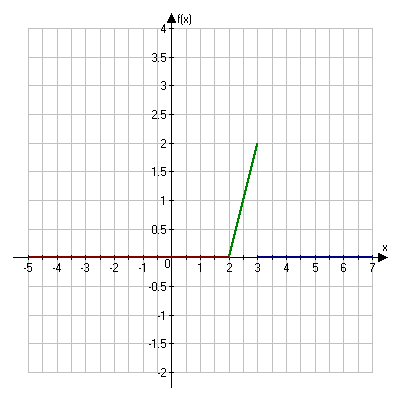 Построим график функции F(x) 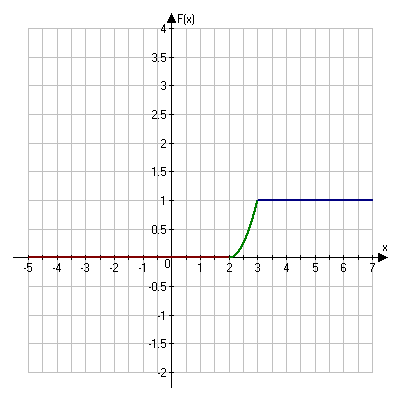 3) Вычислим математическое ожидание 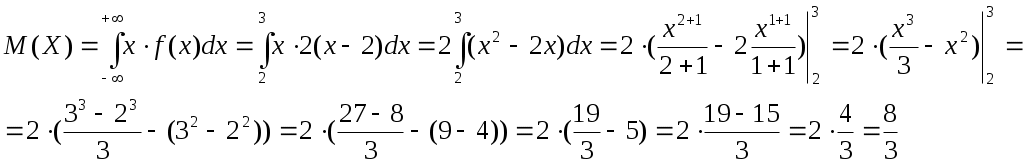 Дисперсию вычислим по формуле Дисперсию вычислим по формуле 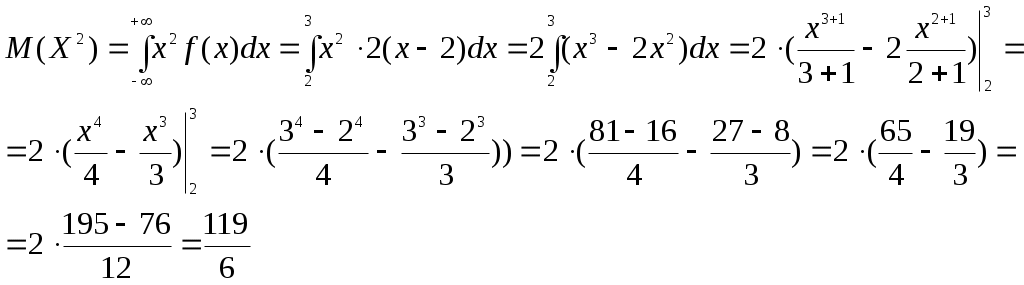 Среднеквадратическое отклонение равно 4) Вероятность попадания на интервал ( Ответ: 1) 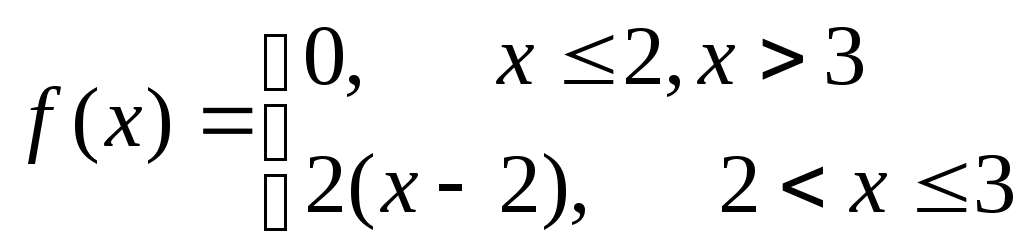 ,3) ,3) 4) №31 Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя Решение. 1) Для определения доверительного интервала для математического ожидания воспользуемся формулой По таблице функции Лапласа из соотношения найдем Определим точность оценки Следовательно, доверительный интервал будет 2) Так как CВ Х распределена нормально, то плотность распределения будет иметь вид 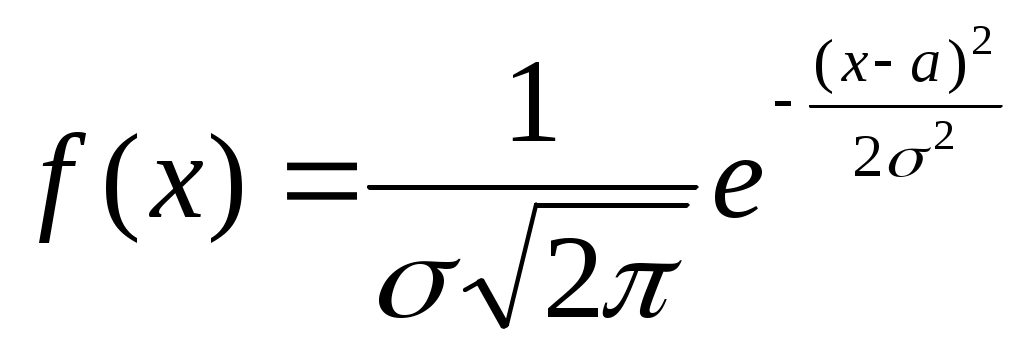 Так как мы принимаем Постоим график 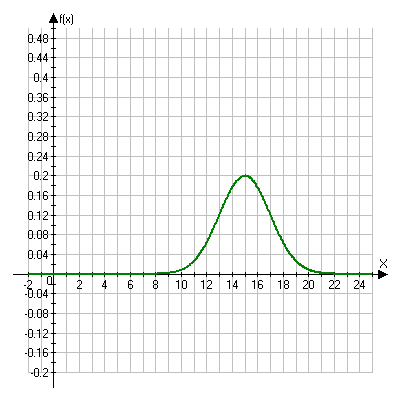 3) По правилу “трех сигм” почти все значения случайной величины Х лежат в промежутке 4) Для нормального распределения функция распределения запишется Вероятность попадания на отрезок 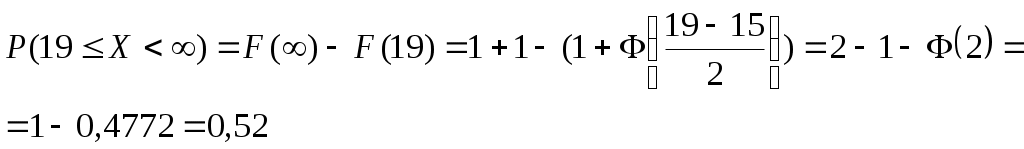 Ответ: 1) 3) №41 Отдел технического контроля проверил n партий изделий и установил, что число Х нестандартных изделий в одной партии имеет следующее эмпирическое распределение, сведенное в таблицу, где n=250; α =0,05
Решение. Находим выборочную среднюю 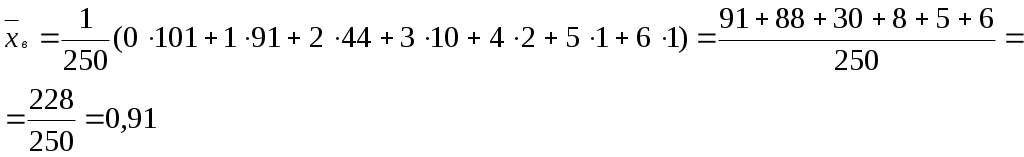 В качестве оценки параметра выберем полученное значение выборочного среднего Проверим гипотезу о том, что случайная величина Х распределена по закону Пуассона, пользуясь критерием Пирсона Расчет теоретических частот Расчеты приведем в таблице
Малочисленные частоты
Получили По таблице критических точек распределения Так как Ответ: гипотеза верна № 51 В процессе эксплуатации ЭВМ возникают неисправности (сбои). Поток сбоев считаем простейшим. Среднее число сбоев за сутки равно m. Найти вероятности следующих событий: А - за n суток нет ни одного сбоя; В – за одни сутки будет хотя бы один сбой; С – за неделю произойдет не менее k сбоев. Решение. Решение задачи будем искать по формуле Где m- среднее число сбоев за сутки, к- количество сбоев за сутки, t- количество суток. Рассмотрим событие А - за 2 суток (t=2)нет ни одного сбоя (к=0). Тогда вероятность этого события равна Вероятность события В – за одни сутки (t=1) будет хотя бы один сбой найдем как вероятность противоположного события Тогда Найдем вероятность того, что за неделю произойдет не менее 3 сбоев (событие С). Воспользуемся свойством вероятности противоположных событий Где событие 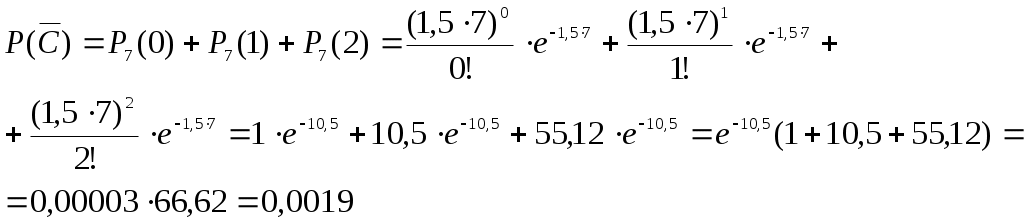 Тогда Ответ: №61 Задана матрица вероятностей перехода дискретной цепи Маркова из i-го состояния в j-ое за один шаг (i, j=1, 2). Распределение вероятностей по состояниям в начальный момент t=0 определяется вектором матрицу Р2 перехода цепи из состояния i в состояние j за два шага; распределение вероятностей по состояниям в момент t=2; вероятность того, что в момент t=1 состоянием цепи будет i=2; стационарное распределение. Решение. 1) Для дискретной цепи Маркова в случае ее однородности справедливо соотношение где Р1 – матрица переходных вероятностей за один шаг; Рn - матрица переходных вероятностей за n шагов; Найдем матрицу Р2 перехода за два шага 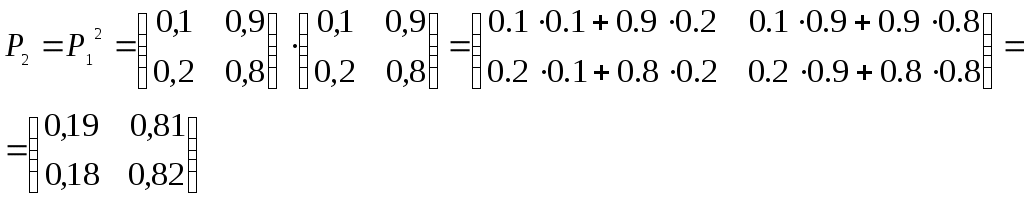 2) Распределение вероятностей по состояниям в момент t=2 определяется формулой так как из состояния в момент времени t=0 в состояние в момент времени t=2 система переходит за два шага. 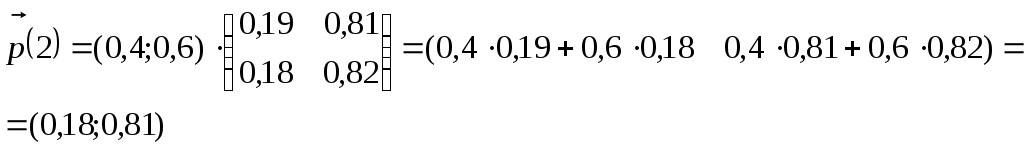 3) Распределение вероятностей по состояниям в момент t=1 определяется формулой 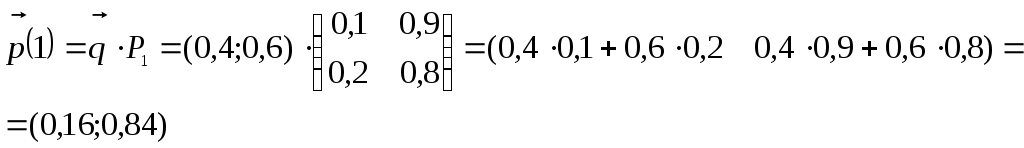 Вероятность того, что в момент t=1 состоянием цепи будет i=2 равна р2(1)=0,84. 4) Для определения стационарного распределения вероятностей составляем систему уравнений 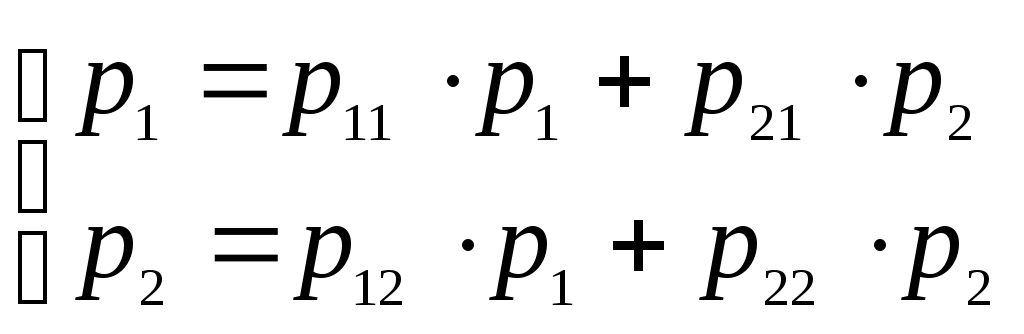 Где 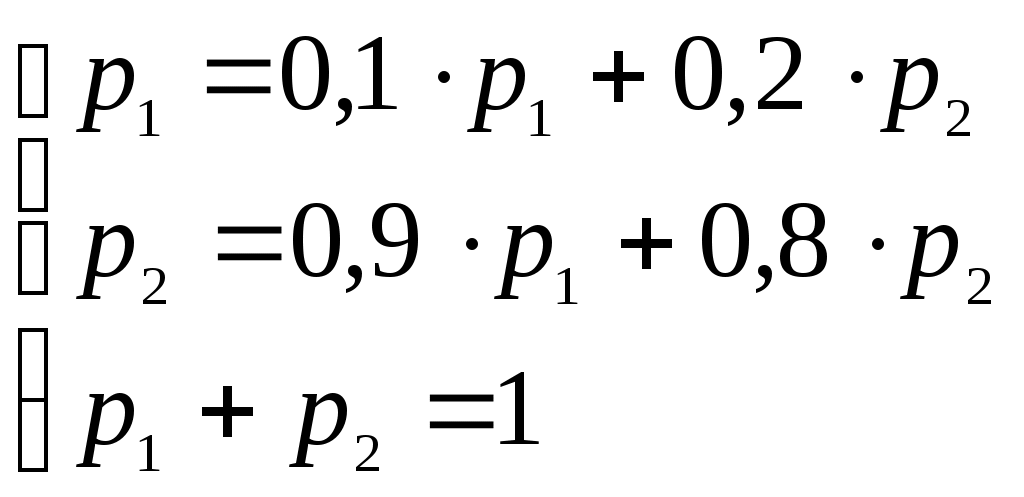 , , 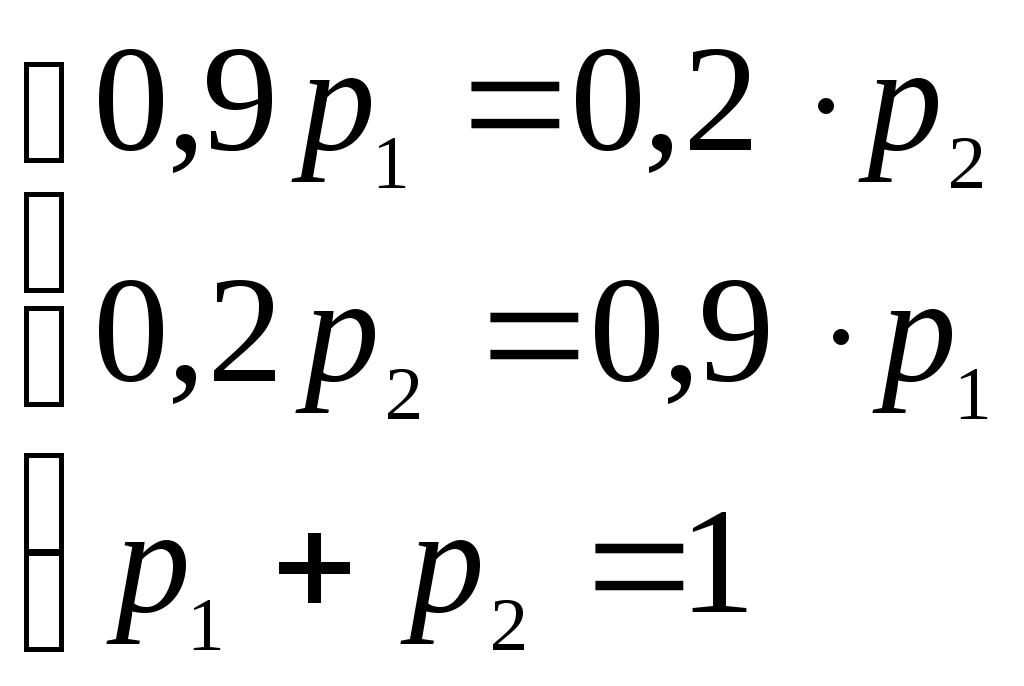 , , 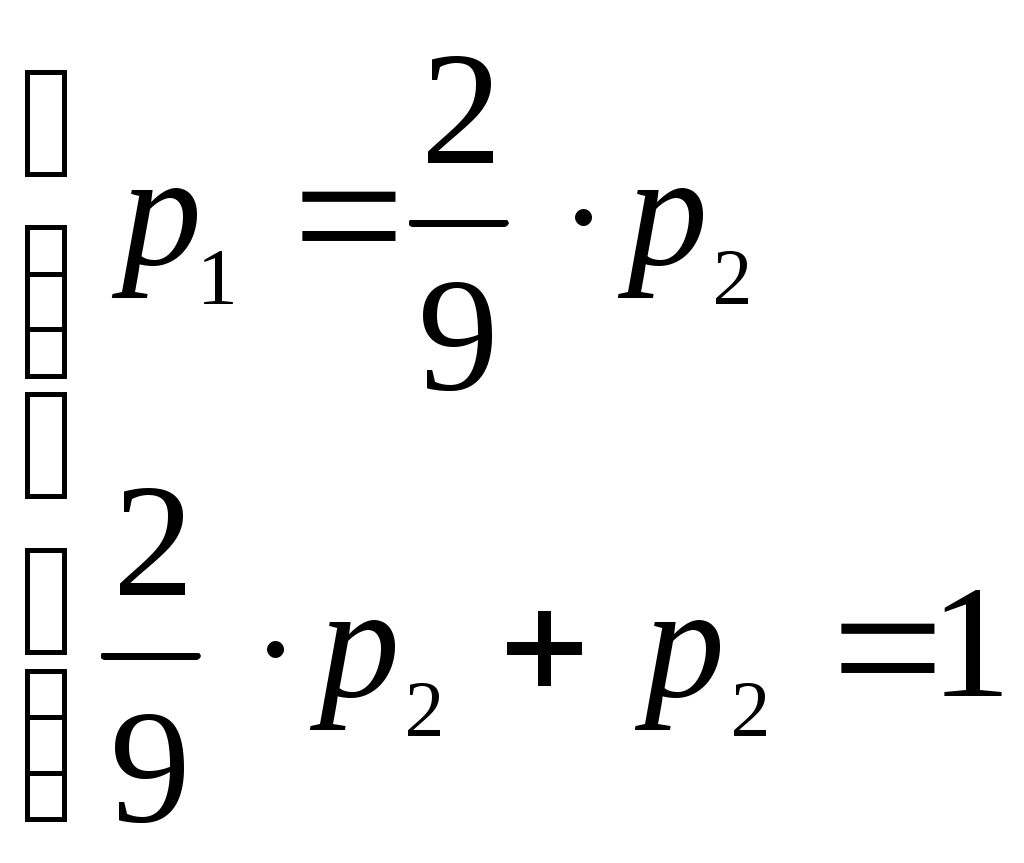 , , 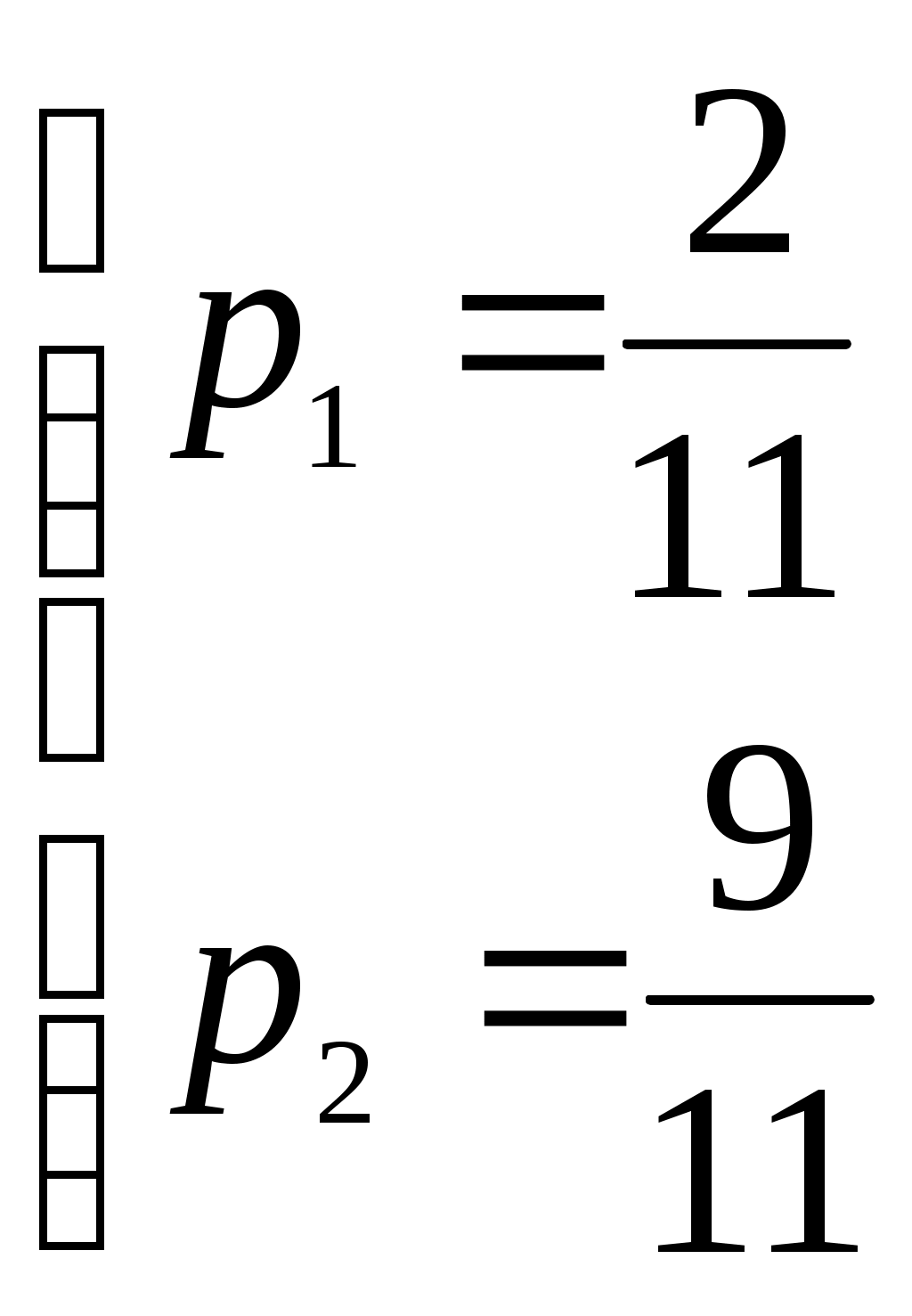 Следовательно, Ответ: 1) 4) №81 Найти спектральную плотность стационарной случайной функции Х(t), если ее корреляционная функция имеет вид 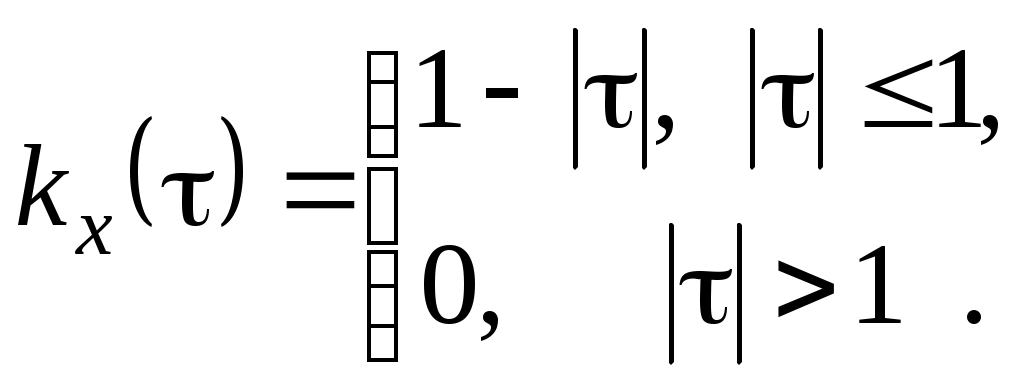 Решение: Спектральную плотность будем находить по формуле Учитывая, что 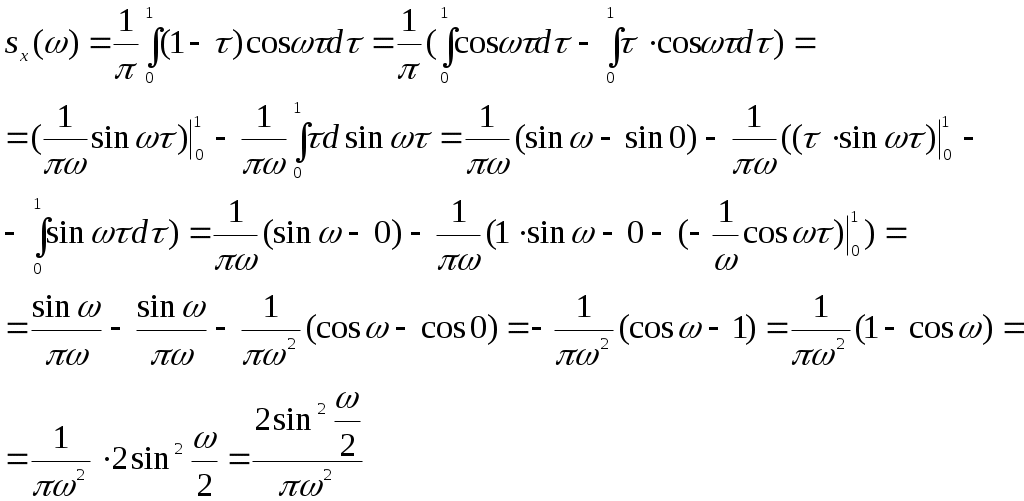 Ответ: Ответ: 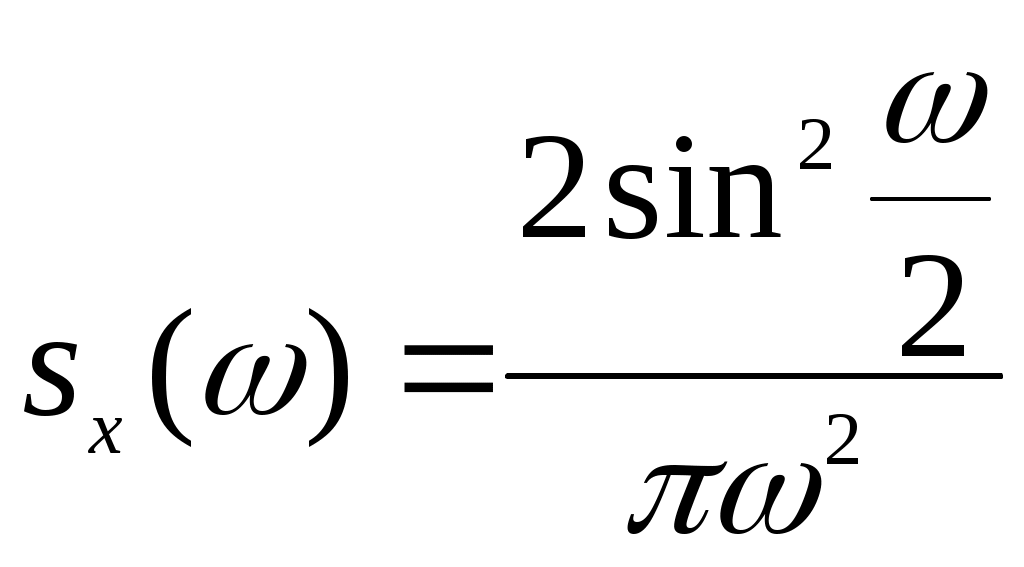 91.На вход линейной стационарной динамической системы, описываемой данным дифференциальным уравнением, подается стационарная случайная функция Х(t) с математическим ожиданием mx и корреляционной функцией kx(τ). Найти: 1) математическое ожидание; 2) дисперсию случайной функции Y(t) на выходе системы в установившемся режиме. Решение. Найдем математическое ожидание, используя формулу: В данном случае Найдем спектральную плотность где Найдем передаточную функцию, для чего напишем заданное уравнение в операторной форме: 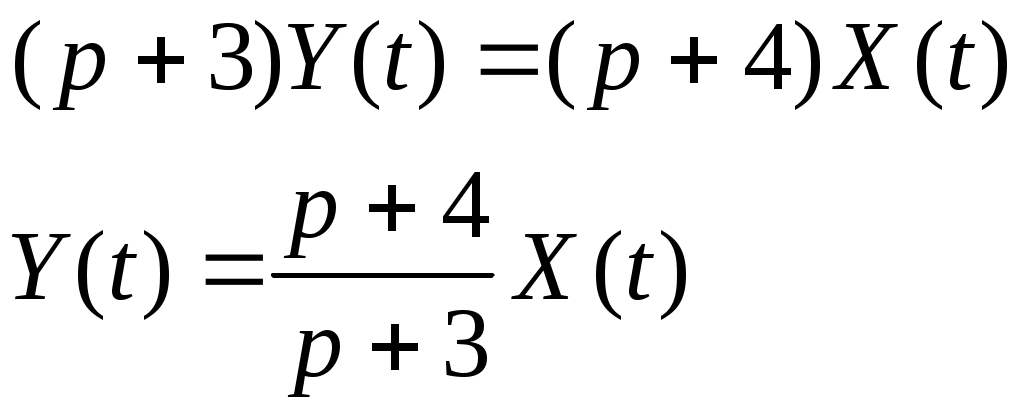 Cледовательно, передаточная функция: Найдем частотную характеристику, для чего заменим в передаточной функции аргумент р на iw: Найдем спектральную плотность выходной функции, для чего умножим спектральную плотность входной функции на квадрат модуля частотной характеристики: 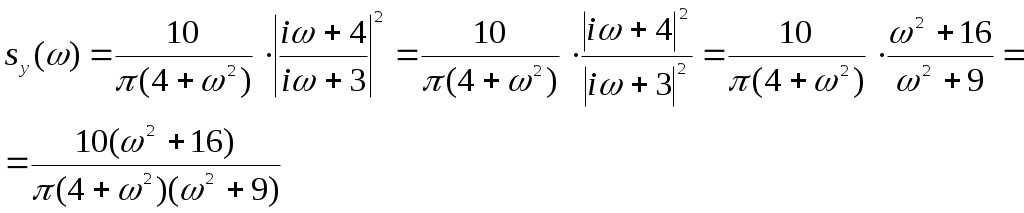 Найдем искомую дисперсию: Представим дробь Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество: 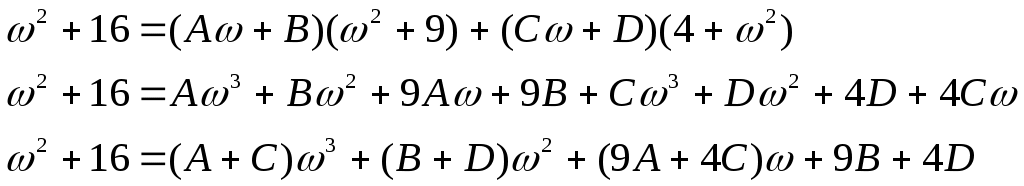 Найдём искомые коэффициенты из системы: 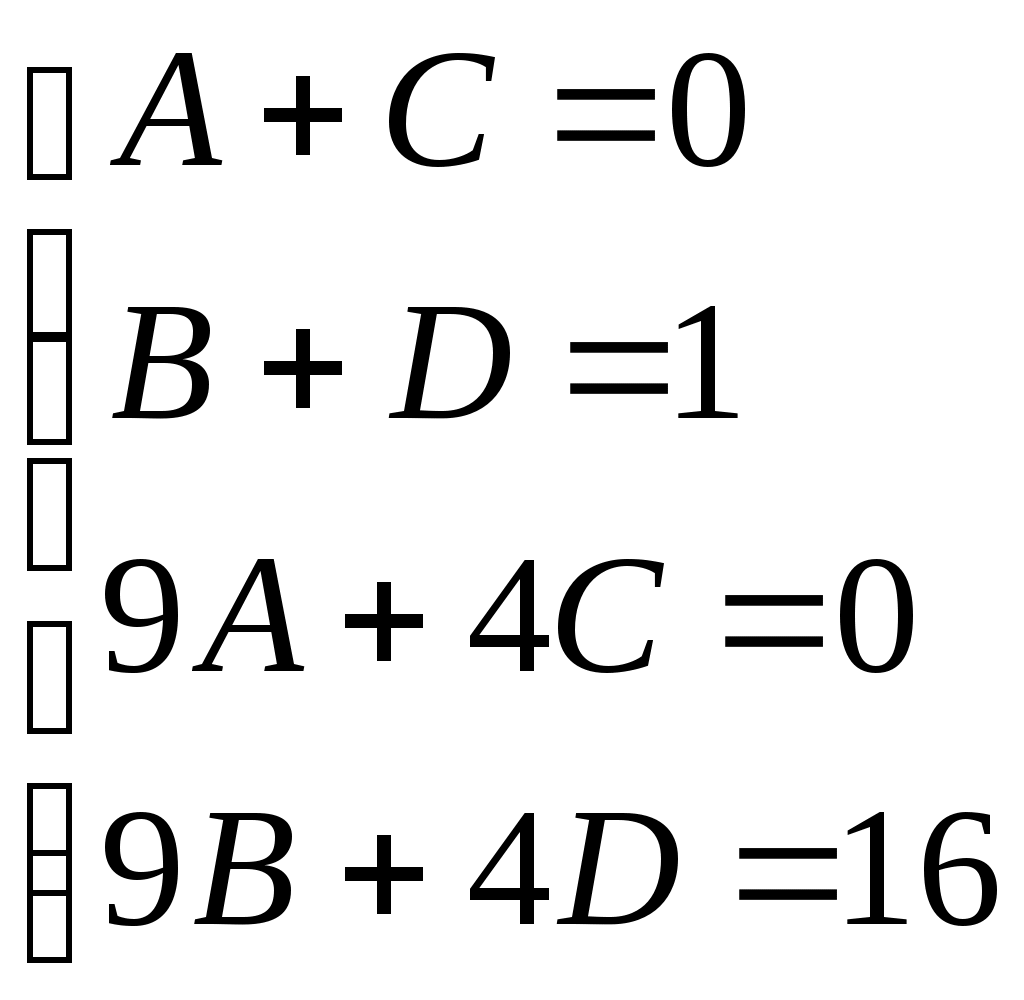 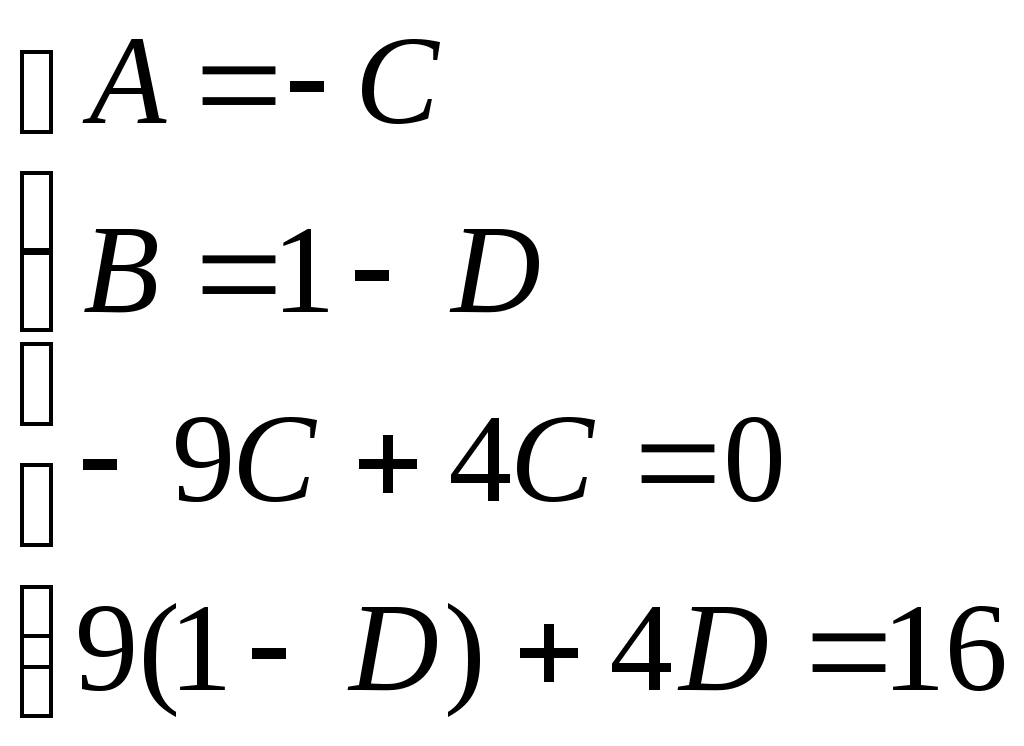 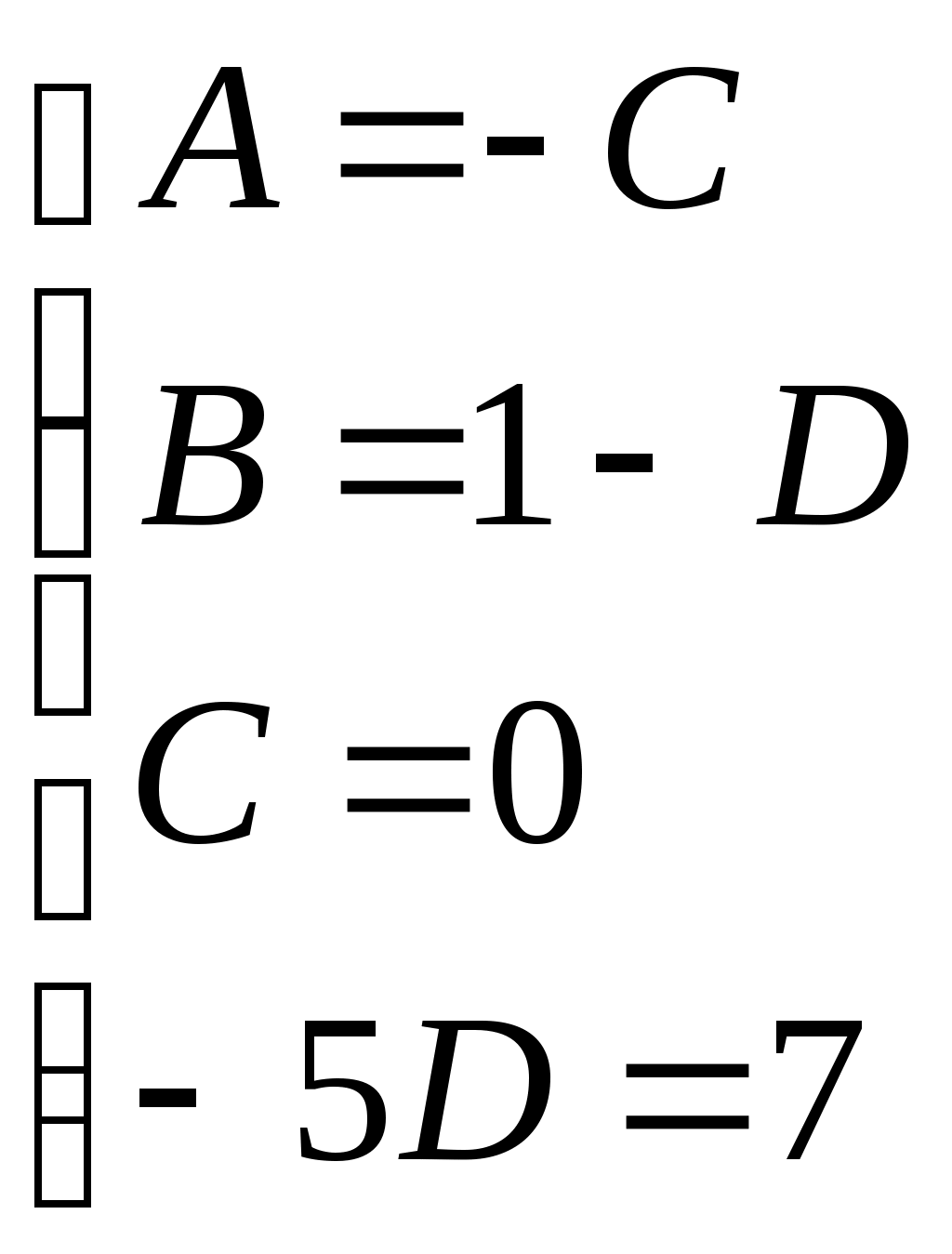 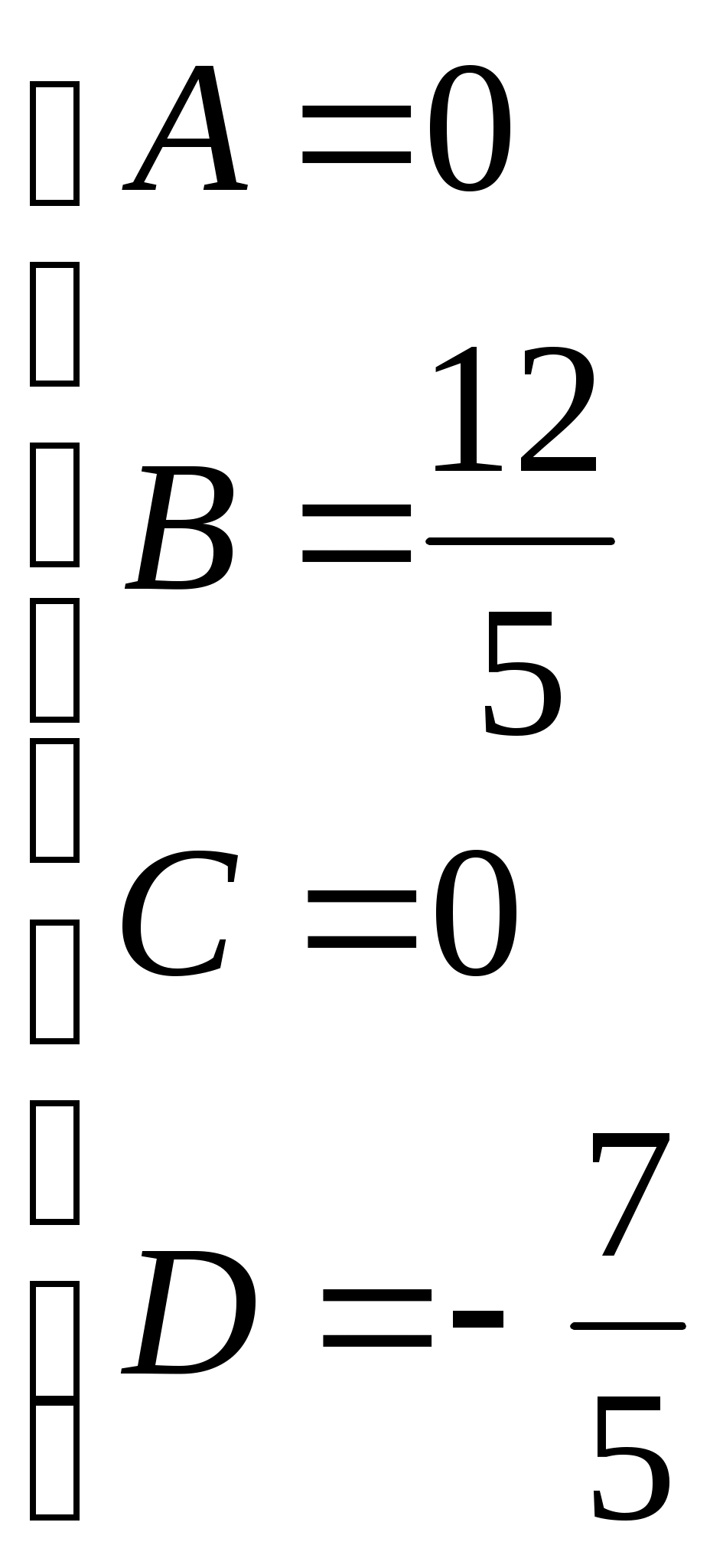 Тогда 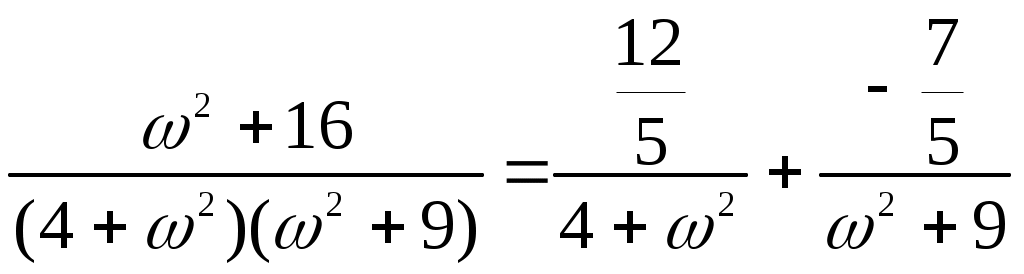 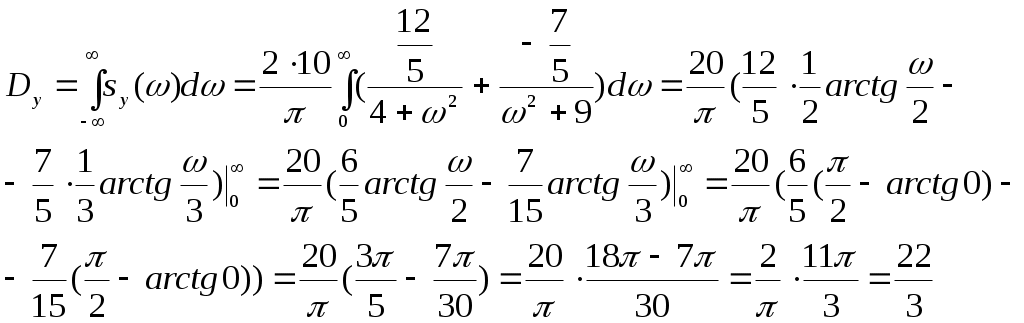 Ответ: Помощь на экзамене онлайн. |
