Решение задач по статистике, контрольные и курсовые работы
 Скачать 173 Kb.
|
|
Решение задач по статистике, контрольные и курсовые работы. Задача 7. Плановый выпуск продукции в отчетном периоде должен был составить 6 млн. руб. при средней списочной численности работающих 1259 человек и общем фонде заработной платы 1450 тыс. руб. Фактически фабрикой выпущено готовой продукции на 6,2 млн. руб. при средней списочной численности работающих 1225 человек и общем фонде заработной платы 1479 тыс. руб. Определить относительные величины выполнения плана: 1) выпуска готовой продукции; 2) средней численности работающих; 3) расходования заработной платы. Изобразите в виде полосовой диаграммы выполнение плана по выпуску готовой продукции, средней численности работающих и расходованию фонда заработной платы. Решение. 1. Определим относительную величину выполнения плана по выпуску готовой продукции: ОТВВП(ГП) = (ГПфакт/ГПпл)∙100% = (6,2/6)∙100% = 103,3% 2. Определим относительную величину выполнения плана по средней численности работающих: ОТВВП(S) = (Sфакт/Sпл)∙100% = (1225/1259)∙100% = 97,3% 3. Определим относительную величину выполнения плана по фонду заработной платы: ОТВВП(ФЗП) = (ФЗПфакт/ФЗПпл)∙100% = (1479/1450)∙100% = 102% В отчетном периоде план по выпуску готовой продукции был перевыполнен на 3,3%, средняя численность работающих по сравнению с плановой оказалась на 2,7% меньше, а фонд заработной платы превысил плановый на 2%. Изобразим в виде полосовой диаграммы выполнение плана по выпуску готовой продукции, средней численности работающих и расходованию фонда заработной платы. 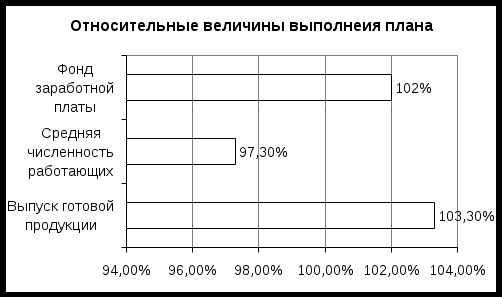 Задача 14. Имеются данные о распределении заводов цементной промышленности по размеру производственных мощностей.
Вычислить среднее производство цемента в год на одном заводе. При расчетах принять значение варианта для первой группы равным 70. Определите моду и медиану. Решение. Для того чтобы вычислить среднее значение признака перейдем от интервального ряда к дискретному, т.е. найдем середину каждого интервала как полусумму нижней и верхней границ. При этом согласно условию задачи значение варианта для первой группы примем равным 70, а величина открытого интервала последней группы приравняем к величине интервала предпоследней группы. Для удобства вычислений составляем таблицу. Помощь на экзамене онлайн.
Найдем среднюю величину производства цемента:  = 33230/100 = 332,3 тыс. т.Найдем моду Мо и медиану Ме: Мо=ХМо + iМо 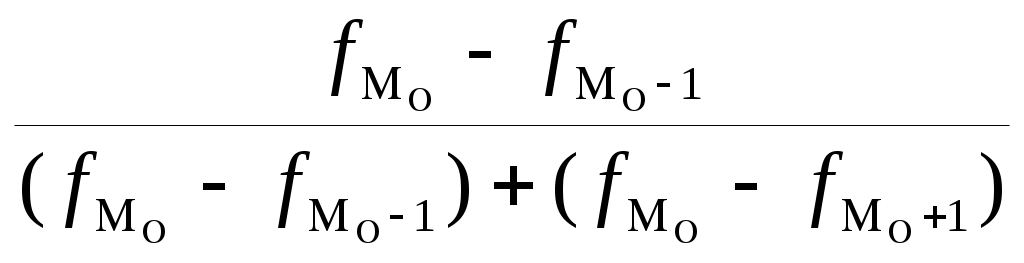 =200+ тыс. т. fM0,fM0-1,fM+1 –частоты модального ,до и после модального интервалов соответственно,ХМ0 – начало модального интервала. iМО- величина модального интервала. Мода показывает варианту, наиболее часто встречающуюся в данной совокупности. Наибольшее число заводов в рассматриваемой совокупности имеют величину годового производства цемента равную 245 тыс. т. Ме=ХМе + iМе 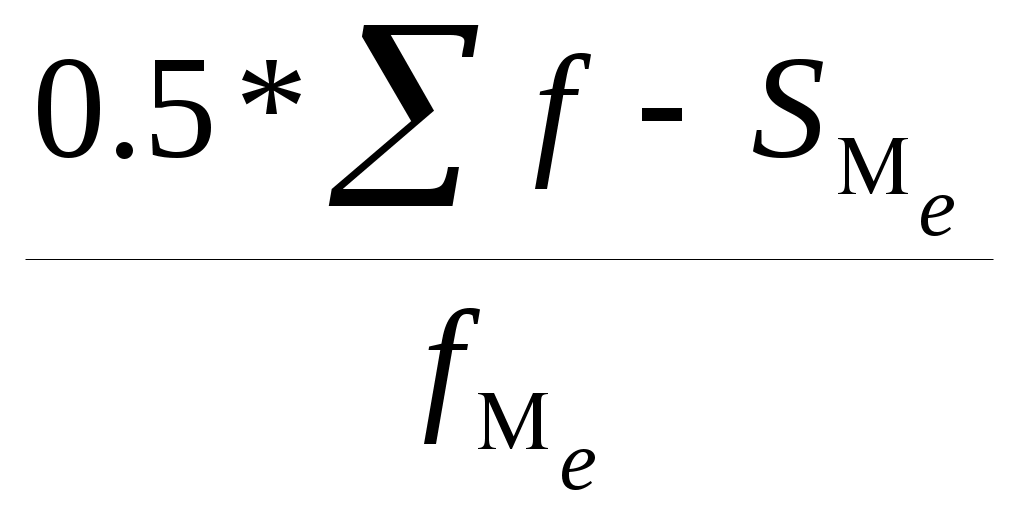 = тыс. т.ХМе- начало медианного интервала; iМе - величина медианного интервала;SМе- сумма накопленных частот до медианного интервала: fМе – частота медианного интервала. Медиана – это варианта, располагающаяся в середине ранжированного ряда распределения. Медиана – это варианта располагающаяся в середине ранжированного ряда распределения. Половина заводов имеют величину годового производства цемента до 266,7 тыс. т., а половина заводов – более 266.7 тыс. т. Задача 21. В результате 5% случайной бесповторной выборки были получены следующие данные о распределении рабочих по стажу:
С вероятностью 0,997 определите предельную ошибку выборочной доли рабочих с длительностью рабочего стажа до 9 лет. Решение. Нужно найти с вероятностью 0,997 предельную ошибку выборочной доли (  ) и границы генеральной доли () рабочих cо стажем работы до 9 лет, по формуле  .Находим общее число рабочих в выборке и выборочную долю: n = 20 + 30 + 70 + 50 + 30 = 200 чел.  =(20+30+70)/200 = 0,6 Предельная ошибка выборочной доли рабочих со стажем до 9 лет: = или 10,1%Так как р=0,997 то t = 3. 60 – 10,1  60 + 10,149,9% 70,1%Итак с вероятностью р=0,997 можно утверждать, что границы генеральной доли рабочих cо стажем работы до 9 лет находятся от 49,9% до 70,1%. Задача 28. Производство цемента характеризуется следующими данными:
На основе приведенных данных определите а) средний уровень ряда б) цепные и базисные темпы роста; в) средний абсолютный прирост. Решение. А) Для определения среднегодового производства цемента за 1990-1999 гг. достаточно найти среднюю арифметическую по формуле:  т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число. Таким образом, среднегодовое производство цемента за 1990-1999 гг. составит:  88,4 млн. т.Б) Темпы роста можно определить с помощью формул: цепные.......................................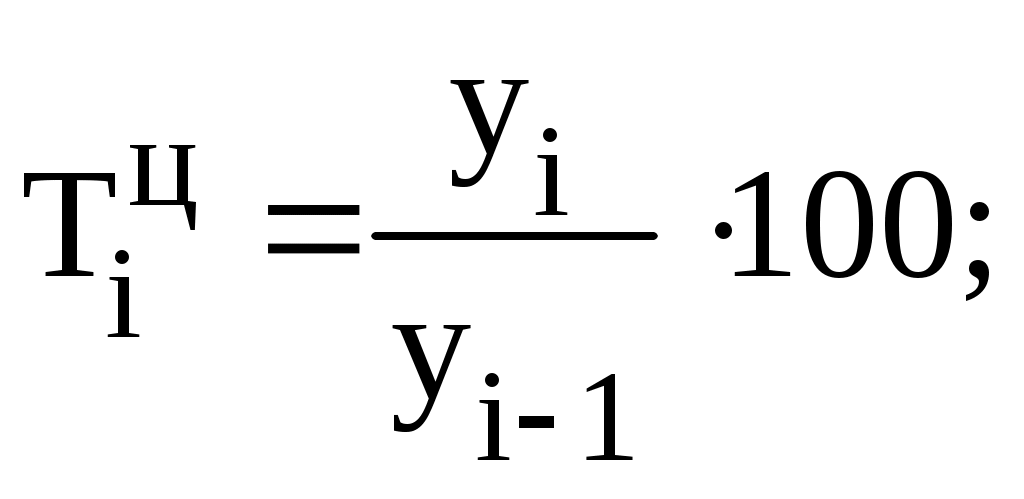....  базисные.......................................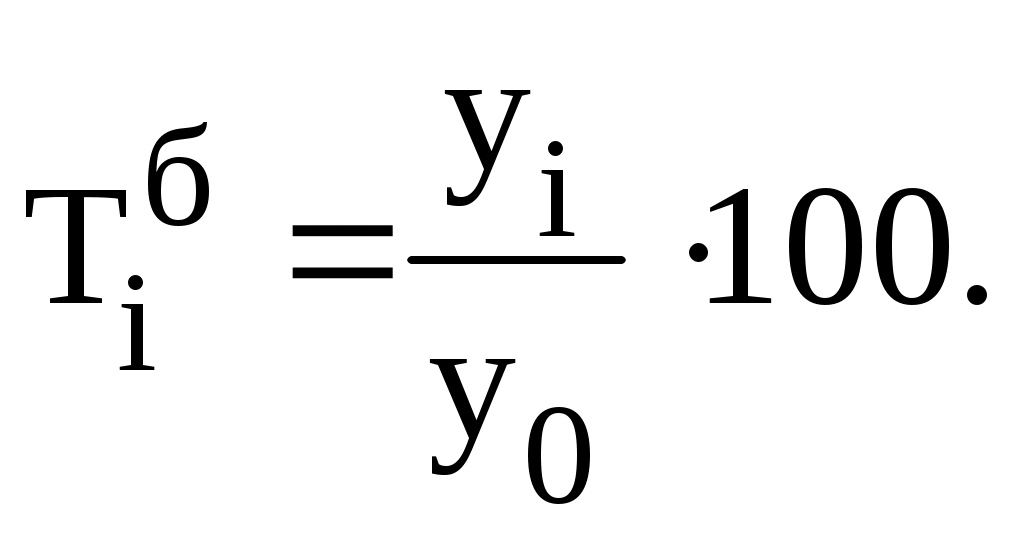...  В 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998 и 1999 годах цепные темпы роста будут составлять:  = 112,5%;  = 111,1%; = 105%;  = 102,4%; = 104,7%;  = 105,6%; = 105,2%;  = 104%; = 104,8%.Базисные темпы роста в 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998 и 1999 годах составят:  = 112,5%;  = 125%; = 131,3%;  = 134,4%; = 140,6%;  = 148,4%; = 156,3%;  = 162,5%; = 170,3%.В) Найдем средний абсолютный прирост по формуле:  где m – число базисных абсолютных приростов; уi – производство цемента в последнем периоде; уо – производство цемента в базовом периоде.  = 5 млн. т.В среднем с 1990 по 1999 годы производство цемента каждый год возрастало на 5 млн. т. Среднегодовое производство цемента с 1990 года по 1999 год составило 88,4 млн. т. Задача 31. По металлургическому заводу имеются следующие данные.
Определить по предприятию среднее изменение цен (индексы цен) на продукцию по сравнению с прошлым годом, а также по сравнению с планом. Решение. Рассчитаем общий индекс цен по сравнению с прошлым годом: 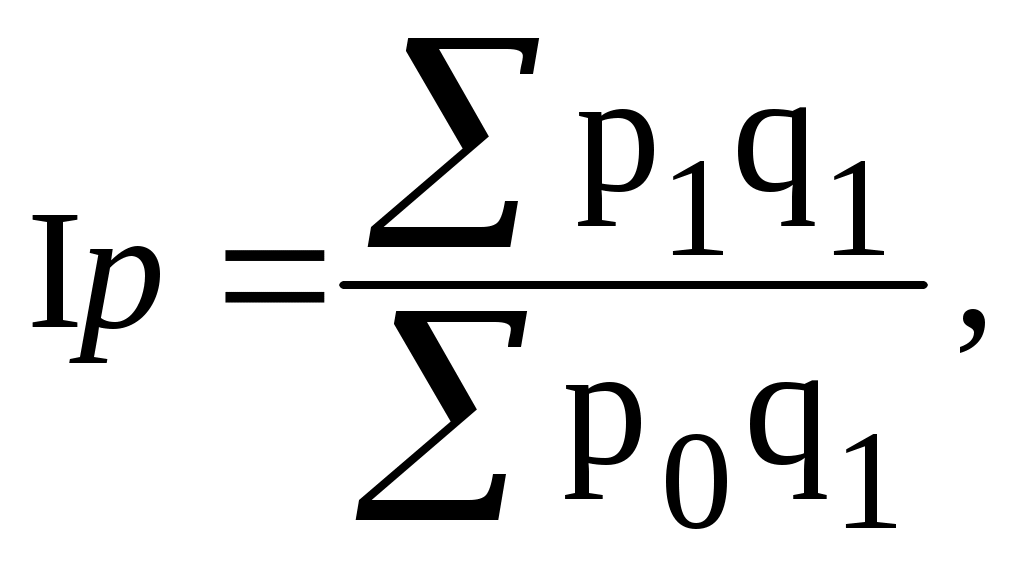 где q – количество единиц данного вида реализованной продукции; p – цена единицы изделия. Подстрочный значок 0 означает базисный, а 1 – отчетный периоды. 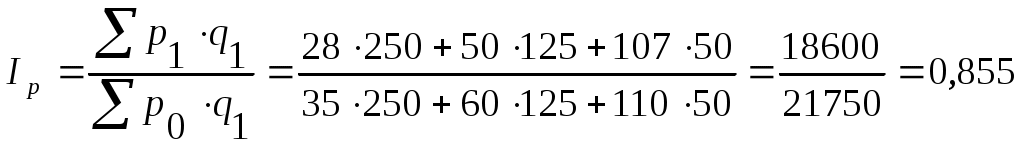 или 85,5%.Рассчитаем общий индекс цен по сравнению с планом: 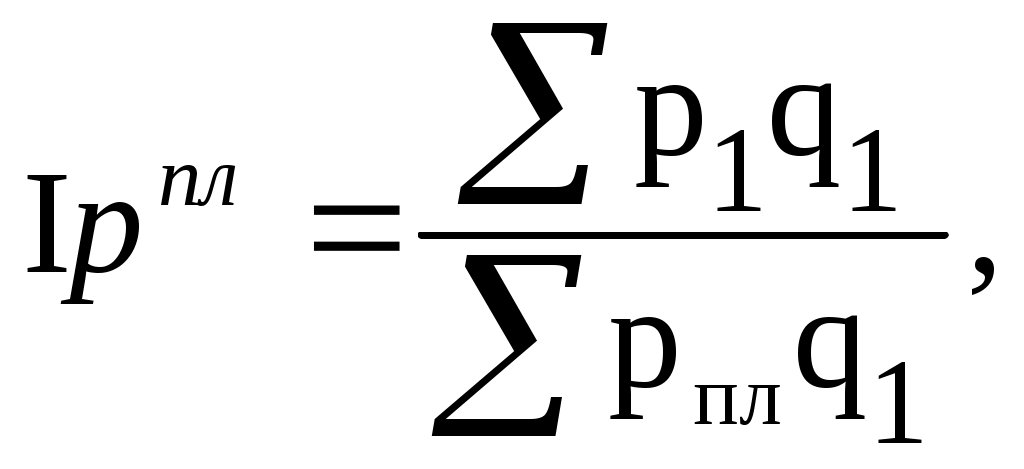 где q – количество единиц данного вида реализованной продукции; p – цена единицы изделия. Подстрочный значок пл. означает план, а 1 – отчетный периоды. 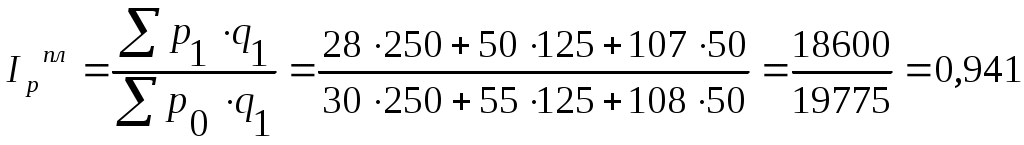 или 94,1%.В отчетном периоде по сравнению с базисным периодом выпуск продукции за счет изменения цен снизился на 14,5%, однако планом предусматривалось снижение на 5,9%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||