Главная страница
Навигация по странице:

  • Цель урока

  • Ход урока Организационный момент.

  • Сообщение темы, цели урока.

  • Проверка домашнего задания.

  • Актуализация опорных знаний.

  • Выполнение заданий обобщающего и систематизирующего характера. 1. Решите в тетрадях самостоятельно задачу 1


  • 9.

    		•

    Решение задач по теме Параллельность прямой и плоскости


    Скачать 71.06 Kb.
    НазваниеРешение задач по теме Параллельность прямой и плоскости
    Дата31.10.2022
    Размер71.06 Kb.
    Формат файлаdocx
    Имя файлаparallelnost_pryamoy_i_ploskosti.docx
    ТипРешение
    #764519

    Конспект урока по геометрии 10 класс.

    Геометрия 10 – 11 классАтанасян Л.С., 2013 год.

    Базовый уровень обучения.

    Тема: Решение задач по теме «Параллельность прямой и плоскости»

    Общее количество часов, отведенное на изучение темы – 1 ч.

    В соответствии с учебным планом и календарно-тематическим планированием урок изучается в теме «Параллельность прямой и плоскости» и следует за уроком изучения нового материала.

    Цель урока: формирование умений учащихся применять признак параллельности прямой и плоскости к решению задач.

    Задачи урока:

    а) образовательные:

    • повторить теоретический материал по теме «Параллельность прямой и плоскости»;

    • закрепить умения: решать задачи на доказательство, опираясь на точные аргументы(знания теоретического материала);

    • при решении стереометрических задач применять знания, полученные при изучении планиметрии;

    • при выполнении рисунка к задаче учитывать наглядность и правила изображения пространственных фигур

    б) развивающие: развитие навыков

    • самостоятельной работы,

    • пространственного мышления, логического мышления;

    в) воспитательная: воспитывать у учащихся

    Тип урока: урок обобщения и систематизации знаний, умений и навыков.

    Техническое обеспечение урока: компьютер, проектор, презентация.
    Содержание урока


    1. Организационный момент. (1-2 мин)

    2. Сообщение темы, цели урока. (1 мин)

    3. Проверка домашнего задания. (3-4 мин)

    4. Актуализация опорных знаний. ( 7 мин)

    5. Выполнение заданий обобщающего и систематизирующего характера.(20 мин)

    6. Формулирование выводов по изученному материалу.(7 мин)

    7. Оценка результатов урока. (3 мин)

    8. Подведение итогов. (3 мин)

    9. Домашнее задание. (3-4 мин)


    Ход урока

    1. Организационный момент.

    Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.

    (В. Произволов). Слайд 2.

    Сегодня на уроке нам предстоит пережить много приключений.

    1. Сообщение темы, цели урока.

    Учитель сообщает тему, цель урока и обращает внимание учащихся на экран.

    Слайд 3.

    1. Проверка домашнего задания.

    Учитель отвечает на вопросы учащихся по домашнему заданию, на слайд выводит верные ответы. Проходит обсуждение решения № 17, № 18(б). Слайд 4.

    1. Актуализация опорных знаний.

    Один ученик у доски доказывает признак параллельности прямой и плоскости.

    Остальные отвечают на вопросы:

    1. Какие две прямые в пространстве называются параллельными?

    2. Сформулируйте теорему о параллельных прямых.

    3. Какие возможны случаи взаимного расположение прямой и плоскости?

    4. Какие прямая и плоскость называются параллельными?

    5. Сформулируйте признак параллельности прямой и плоскости.

    6. Дан куб А... D1. Назовите четыре пары параллельных прямых и четыре пары пересекающихся прямых.

    Выслушивается доказательство теоремы.

    Провести коллективное обсуждение результатов написания математического диктанта.

    1. Выполнение заданий обобщающего и систематизирующего характера.

    1. Решите в тетрадях самостоятельно задачу 1.

    Дана трапеция АВСД с основаниями АД и ВС.

    Через середины боковых сторон проведена плоскость α.

    Докажите, что α. || АД. Слайд 5.

    Можно вызвать ученика к доске решать задачу на закрытой от учащихся части доски.

    Затем учащиеся обсуждают и проверяют решение. Слайд 6.

    2. Задача 2.Докажите, что если плоскость проходит через прямую,

    которая параллельна второй плоскости,

    и пересекает эту плоскость, то прямая

    пересечения параллельна данной прямой. Слайд 7.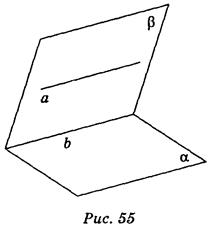


    К доске вызывается ученик и доказывает задачу с наименьшей помощью со стороны учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 8.

    3. Задача №3.Докажите, что если две плоскости пересекаются,

    параллельные одной и той же прямой, то прямая

    пересечения этих плоскостей параллельна данной прямой. Слайд 9.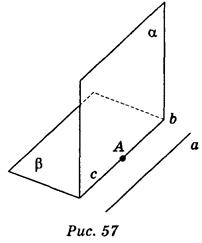



    Сначала рисунок к задаче и доказательство обсуждается с классом. Затем учащиеся записывают доказательство. После того, как задача решена, учитель показывает, как можно было записать доказательство. Слайд 10.

    4. Решить № 26 

    Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны. Слайд 11

    Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.



    Доказательство

    1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).

    2. угол В - общий.

    З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.

    К доске вызывается ученик и доказывает задачу с помощью учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 12.

    5. Решите в тетрадях самостоятельно № 28 

    На сторонах АВ и АС треугольника АВС взяты соответственно точки D и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и С и параллельна отрезку ОE. Найдите длину отрезка ВС. Слайд 13

    Затем учащиеся обсуждают и проверяют решение. Слайд 14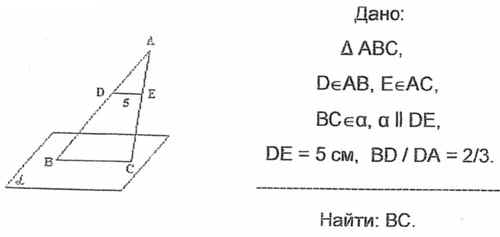



    Решение:

    Из условия задачи № 26: треугольник АВС подобен треугольнику АDЕ.

    Тогда АВ/АD = ВС/DЕ, 5/3 = х/5, х = 25/3, х = 81/3.

    Ответ: 81/3.

    6. Формулирование выводов по изученному материалу.

    Математический диктант. Слайд 15.

    Д 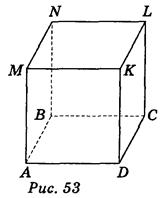ано изображение куба: вариант 1 - рис. 1, вариант 2 - рис. 2.

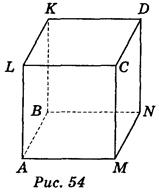    рис.1 рис.2

     

     

    Пользуясь изображением, запишите:

    1) прямую, которая параллельна плоскости ВСМ и проходит через точку D;

    2) грани куба, которые параллельны прямой CD;

    3) плоскость, содержащая прямую ВN и параллельная прямой С,D;

    4) плоскость, параллельная прямой С,D и проходит через точку К;

    5) плоскости, которые параллельны прямой ВМ;

    6) прямые, параллельные плоскости АВМ.

    Ответ. Вариант 1.1) D; 2) АВNМ и МNLК; 3) АВN; 4) КМN и АВК; 5) DСК, LСА, КDM; 6) КL, LС, СD, ЕD, КС, DL.

    Вариант 2.1) DN; 2) АВКL, АВNМ; 3) АВN; 4) АВК и КLМ; 5) СDК, КCN, КСА; 6) KL, LС, СD, KD, KС, DL. Слайд 16.

    7. Оценка результатов урока.

    8. Подведение итогов.

    Вопросы к классу

    1) Сформулируйте признак параллельности прямой и плоскости.

    2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно?

    3) Завершите утверждение.

    а) Если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения ... .

    б) Если через каждую из двух параллельных прямых провести плоскости, которые пересекаются, то их линия пересечения ... .

    в) Если две плоскости, которые пересекаются, параллельные одной и той же прямой, то прямая пересечения этих плоскостей ... .

    9. Домашнее задание.

    Повторить п.1 – 6.

    Решить № 27, № 30, № 31

    написать администратору сайта