задачи с календарем. Решение задач, связанных с датами и календарём
 Скачать 168.06 Kb. Скачать 168.06 Kb.
|
|
Решение задач, связанных с датами и календарём Показываем, как в 4-5 классе решать задачи, связанные с календарем, датами и днями недели. Если ваш ребёнок отправляется на экзамен или олимпиаду, где могут быть задачи, связанные с календарём, убедитесь, что он знает, сколько дней в каждом месяце, помнит про високосные года - что високосный год это тот, который без остатка делится на 4, и что у високосного года в феврале 29 дней, а дней в году 366. Это критически важно для таких задач. На экзамене подсмотреть в календарь в смартфоне будет нельзя. А теперь на конкретных примерах рассмотрим, как решать такие задачи. 1. Задача. Может ли в одном месяце быть 5 четвергов, 5 суббот и 5 воскресений и при каких условиях? Решение В каждом месяце 4 полных недели (28 дней) и, если это не февраль, то ещё 2 или 3 дня. Если это февраль високосного года, то ещё 1 день. Таким образом, в каждом месяце гарантированно 4 раза встречается каждый день недели, и ещё 2 или 3 дня недели могут встречаться 5 раз. Очевидно, что для того, чтобы какой-то день недели гарантированно (кроме февраля) был в месяце 5 раз, надо чтобы первое число этого месяца приходилось на этот день недели, в крайнем случае второе число. Нам надо ответить на вопрос, могут ли в одном месяце одновременно быть 5 четвергов, 5 суббот и 5 воскресений. Хотите, чтобы ваш ребёнок обучался самостоятельно? Вам поможет наш ВИДЕОКУРС Вариант 1. Месяц начинается с понедельника: 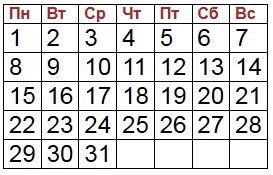 Вариант 2. Месяц начинается с четверга: 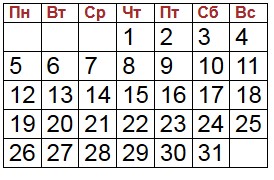 Если первое число месяца приходится на четверг, то пятый четверг приходится на 1 + 7∙4 = 1 + 28 = 29 число. После этого ещё будет одна пятница 30-го числа, и, если в месяце 31 день, то одна суббота. Т.к. нет месяцев, в которых 32 дня, то 5 четвергов и 5 воскресений быть не может. Ответ: 5 четвергов и 5 суббот может быть только если в месяце 31 день, и первое число приходится на четверг. 5 четвергов и 5 воскресений быть не может. 2. Задача В феврале 2008 года 5 пятниц. На какой день недели приходится 21 февраля 2008 года? Решение 2008 – это високосный год, т.е в феврале 29 дней. 5 пятниц может быть только при условии, что 1 февраля приходится на пятницу (вспомним решение предыдущей задачи). Тогда последняя пятница – это 1 + 7∙4 = 29 февраля. Таким образом, если 29 февраля – пятница, то 22 февраля тоже пятница (29 – 7 = 22). Таким образом, 21 февраля – четверг. Ответ: четверг Проверка: 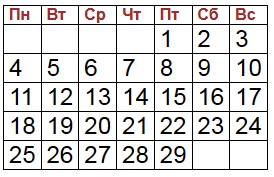 ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы. 3. Задача. В некотором месяце три субботы пришлись на чётные числа. Какой день недели был 11 числа этого месяца? Решение Во-первых, вспомним, что в каждом месяце может быть максимум 5 одинаковых дней недели. И вспомним, что чётное число при сложении с нечётным даёт нечётное число. Так как в неделе 7 дней, то чётные субботы (приходящиеся на чётные числа) чередуются с нечётными – равно как и чётные понедельники чередуются с нечётными и т.д. То есть если у нас максимум 5 одинаковых дней недели в месяце, и из них три пришлись на чётные числа, то это значит, что самый первый такой день недели должен приходиться на чётное число. Таким образом, если у нас первая суббота – чётная, то вторая – нечётная, третья опять чётная, четвёртая нечётная и последняя пятая – чётная. Наименьшее чётное число – это 2. То есть первый день месяца – это пятница, второй день – суббота. Таким образом, 9 число тоже суббота (2 + 7 = 9). Следовательно, 10 – это воскресение, а 11 – понедельник. Ответ: понедельник.4 Итак, на основе решения этих задач мы можем запомнить важные правила, которые пригодятся для решения других задач, связанных с календарём: 1. В месяце гарантированно есть 4 одинаковых дня недели, и может быть максимум 5 одинаковых дней недели. 2. Для того, чтобы в месяце было 5 одинаковых дней недели, надо, чтобы этот день недели приходился на 1 или 2 число месяца. В случае, если в месяце 31 день, то он может приходиться и на 3 число (3 + 7∙4 = 31) 3. Так как в неделе 7 дней (нечётное число), то одинаковые дни недели поочерёдно выпадают на чётные и нечётные числа месяца. Не может быть такого, что два одинаковых дня недели в соседних неделях приходятся оба на чётные или оба на нечётные числа. 4. Зная, сколько всего заданных дней недели в месяце, и сколько из них пришлось на чётные или нечётные числа, мы можем понять, на какое число - чётное или нечётное выпал первый соответствующий день недели в этом месяце. Математические олимпиадные задачи 1. Может ли быть в одном месяце быть 5 понедельников и 5 четвергов? Обоснуйте ответ. Если в месяце 31 день, и он начинается с понедельника, то в нём может быть 5 понедельников, 5 вторников и 5 сред, но остальных дней недели по четыре, так как 5+5+5+4+4+4+4=31. Ответ: не может. 2. В феврале 2004 года 5 воскресений, а всего – 29 дней. На какой день недели приходится 23 февраля 2004 года? Если в феврале 29 дней и 5 воскресений, то первое воскресение будет 1 февраля. Отсюда 23 февраля – понедельник. 3. В некотором месяце три пятницы пришлись на чётные числа. Какой день недели был 15 числа этого месяца? Три пятницы, выпадающие на чётные числа месяца, могут быть только 2, 16 и 30 числа. 15 числа был четверг. 4. Известно. Что 1 декабря приходится на среду. На какой день недели приходится 1 января следующего года? Среда 1, 8, 15, 22, и 29 декабря, четверг 30, пятница 31. Ответ: суббота 1 января следующего года. 5. В некотором месяце три воскресенья пришлись на чётные числа. Какой день недели был 20 числа этого месяца? Четные воскресенья 2, 16, 28. Значит 20 число этого месяца – четверг. 6. Какое наибольшее число воскресений может быть в году? 53 воскресенья. 7. Какое самое большое число месяцев с пятью воскресениями может быть в году? 5 месяцев. Обычный год при этом должен начинаться с воскресенья, а високосный – с субботы или воскресенья. 8. В каком-то году некоторое число ни в одном месяце не было воскресеньем. Какое это могло быть число? 31-е число и только одно. Например, в 2007 году ни одно воскресенье не было 31 числом. 9. В некотором месяце три субботы пришлись на четные числа. Какой день недели был 28-го числа этого месяца? Пусть первая «четная» суббота пришлась на число, которое обозначим через х(х – четное число). Следующая четная суббота будет через две недели, т.е. (х+14) –го числа, а третья «четная» суббота – (х+28) –го числа. Но в месяце не более 31 дня, следовательно, х+28≤ 31. У этого неравенства одно чётное решение х=2. Тогда третья «четная» суббота была 30-го числа, а 28-го был четверг. 10. В некотором месяце три пятницы пришлись на четные числа. Какой день недели был 15 числа этого месяца? 11. В некотором месяце три воскресенья пришлись на четные числа. Какой день недели был 20 числа этого месяца? 12. Докажите, что первый и последний день 2010 года – это один и тот же день недели. 2010 год не високосный 2. Обычный год содержит 365=52х7+1 дней, т.е. 52 полных недели плюс один день. Поэтому любой обычный год начинается и заканчивается на один и тот же день недели. Для 2010 года это будет пятница. 13. В некотором месяце понедельников больше, чем вторников, а воскресений больше, чем суббот. Какой день недели был 5-го числа этого месяца? Мог ли этот месяц быть декабрем? За 4 недели, с 1 по 28-е число, каждый день недели встречается ровно 4 раза, поэтому из условия следует, что 29-е – воскресенье, 30-е – понедельник, а 31-го числа в этом месяце нет. Следовательно, месяц, о котором идет речь, начался с воскресенья, а его 5-е число было четвергом. Данный месяц декабрём быть не мог: в декабре 31 день. РЕКЛАМА Узнать больше РЕКЛАМА 14. В некотором году три месяца подряд содержали всего по четыре воскресенья. Докажите, что один из этих месяцев – февраль. Если февраль не входит в указанные «три месяца подряд», то сумма дней – 91 или 92. Но 91=7х13, 92=7х13+1, т. е в этом случае три месяца содержат 13 полных недель, значит, и каждый день недели, в том числе воскресенье, содержится 13 раз, и условие не выполняется. Тем самым доказано, что один из трех месяцев должен быть февралём, причем в обычном году достаточно, чтобы из трёх месяцев был февралём, а в високосном – эти три месяца: февраль (29), март (31), апрель (30). К тому же необходимо, чтобы последний день третьего месяца был субботой. 15. У большинства Петиных одноклассников день рождения в 1995 году пришёлся на четверг. В 1996 году у большинства одноклассников он пришёлся на пятницу. А на какой день недели он приходился в 1997 году? 1995 и 1997 годы не високосные (по 365 дней), а 1996 – високосный (366 дней). При переходе от 1995 года к 1996 году любое число сместится на один день недели вперёд. Но при переходе от 1996-го високосного, смещение будет на два дня вперёд, т. е. день рождения, приходившийся на пятницу, сместится на воскресенье. 16. Один человек обнаружил в 1937 году, что в Х-м году ему было х лет, и сказал: «Если к числу моих лет прибавить порядковый номер месяца моего рождения, то получится квадрат дня моего рождения. Когда родился этот человек? Если человек жил в 1937 году, то в 1849 году ему не могло быть 43 года: 1849=432. Следующая возможность – ему было 44 года в 1936 году: 1936=442. В силу заданных условий, 44+m=d2; 0 17. Возраст некоего человека в 1989 году был равен сумме цифр года его рождения. В каком году родился этот человек и сколько ему было лет в 1989 году? Пусть его возраст в 1989 году равнялся аb=10a+b. Год его рождения будет 19(8–а) (9–b). По условию имеем 10а+b=1+9+(8–a) +(9–a), 11а+2b=27. Так как 2b чётно, а 27 – нечётное, то 11а – нечётно, т. е ему 18 лет, а родился он в 1971 году. 18. Два не високосных года идут подряд. В первом из них понедельников больше, чем сред. Какой из семи дней недели чаще всего встречается во втором году. Первый год содержит больше понедельников, значит, он начинается и им заканчивается; второй год начинается со вторника, значит им же заканчивается. Значит, вторников будет 53. 19. В феврале 2000 года 2 февраля было средой. Сколько вторников было в феврале 2000 года. Если 2 февраля среда, то 1 февраля будет вторник. Вторник будет и 8, 15, 22, 29 февраля (2000 год високосный). 20. Иван Царевич сказал: «Когда послезавтра станет «вчера», тогда «сегодня» будет так же далеко от воскресенья, как и в тот день, когда послезавтра было завтра». В какой день недели — это сказано? Ответ: воскресенье. 21. Владелец одной фирмы придумал интересную систему отпусков для сотрудников: сотрудники фирмы уходят в отпуск на целый месяц, если этот месяц начинается и кончается одним днём недели. Кому это выгодно? Сколько месяцев сотрудники будут отдыхать с 1 января 2005 года по 31 декабря 2015 года? Для этого в месяце должно быть 29 дней. Это возможно только в феврале високосного года. В названный промежуток попадают только два года: 2008 и 2012. Так что сотрудникам придется отдыхать всего два месяца за эти годы. |
