Поиск кратчайшего пути в Excel. Решение задач в Excel
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
Решение задач в Excel Нахождение кратчайшего пути Определим кратчайший путь между вершинами 1 и 7 на представленном графе. 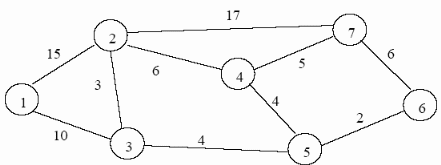 Составим таблицу. Номера вершин от 2 до 7 расположим по горизонтали. Это пункты назначения, то есть вершины, в которые мы придем. Вершины от 1 до 6 расположим по вертикали – это исходные пункты. Пункты назначения начинаем нумеровать со второго, так как вершина 1 – это исходный пункт и в него прийти нельзя. Исходные пункты нумеруем от 1 до 6, так как пункт 7 – конечный и выход из него невозможен.  Внутри таблицы запишем расстояния. Так расстояние из вершины 1 в вершину 2 равно 15, значит на пересечении строки «исходный пункт1» и столбца «пункт назначения 2» ставим число 15. Расстояние из вершины 1 в вершину 3 равно 10, значит на пересечении строки «исходный пункт1» и столбца «пункт назначения 3» ставим число 10. 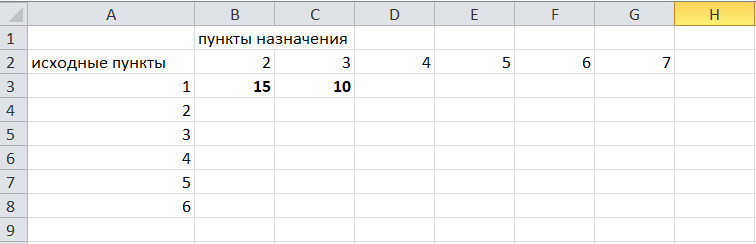 По графу видим, что из вершины 2 можно попасть в вершину 3 (это расстояние равно 3)или в вершину 4 (расстояние равно 6), или в вершину 7 (расстояние равно 17). На пересечении строки «исходный пункт 2» и столбца «пункт назначения 3» ставим число 4. На пересечении строки «исходный пункт 2» и столбца «пункт назначения 4» ставим число 6. На пересечении строки «исходный пункт 2» и столбца «пункт назначения 7» ставим число 17. 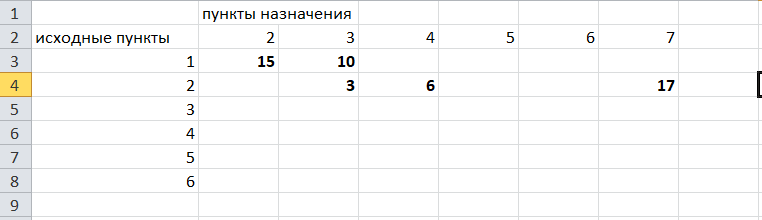 Аналогично заполним в таблицу расстояния из вершины 3 в вершины 2 и 5, которые соответственно равны 3 и 4.  По графу мы видим, что из вершины 4 можно попасть в вершины 2,5,7, расстояние до которых соответственно равны 6,4,5. Занесем эти числа в таблицу:  По графу мы также видим, что из вершины 5 можно попасть в вершины 3,4, 6, расстояние до которых соответственно 4,4,2. 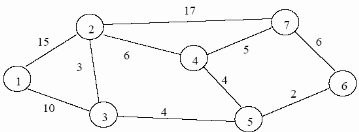 А из вершины 6 можно попасть в вершины 5 и 7, расстояния до которых 2 и 6. Занесем эти расстояния в нашу таблицу:  Путь из вершины 2 в вершину 2, из 3 в 3 и т.д. будет равен 0. Занесем эти величины в таблицу: 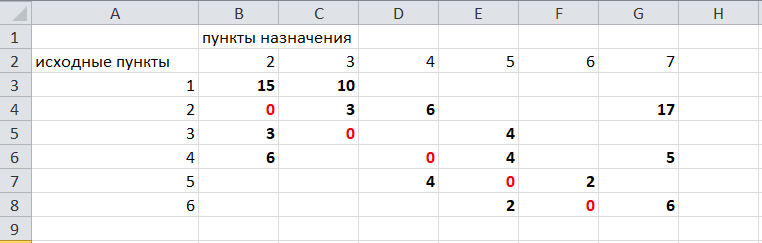 Пустые клеточки в нашей таблице говорят о том, что пути в некоторые вершины нет. Например, рассмотрим строку «исходный пункт 1». Из пункта 1 нет пути в пункты назначения 4,5,6,7. Но оставить соответствующие клетки пустыми мы не можем. Поэтому, чтобы программа поиска решения в Excel начала правильно работать, мы в эти ячейки запишем числа, намного большие самого большого из уже записанных. Тогда, так как мы будем искать кратчайший путь, программа эти значения будет отбрасывать. Например, так как самое большое число в таблице 15, а 100 > 15, мы в пустые ячейки таблицы запишем 100 (Можете записать 500 или 1000, любое число, которое вам нравится). Получим таблицу: 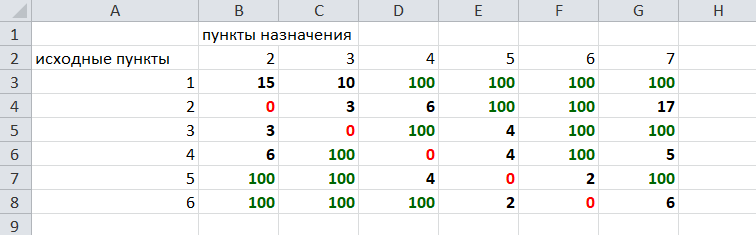 (Цвет записи чисел менять необязательно!) Теперь составим вторую таблицу «План перемещения по кратчайшему пути». Начало работы по составлению таблицы полностью совпадает с составлением первой таблицы, но внутреннюю часть таблицы заполнять не будем. Записываем пункты назначения по горизонтали и исходные пункты по вертикали, но вставим дополнительную строку и дополнительный столбец «наличие», которые заполним единицами. 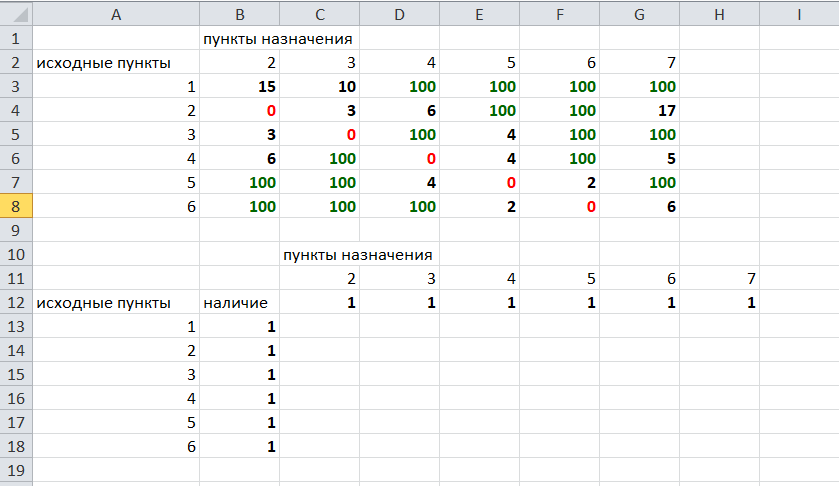 В строке внизу таблицы найдем суммы по столбцам: 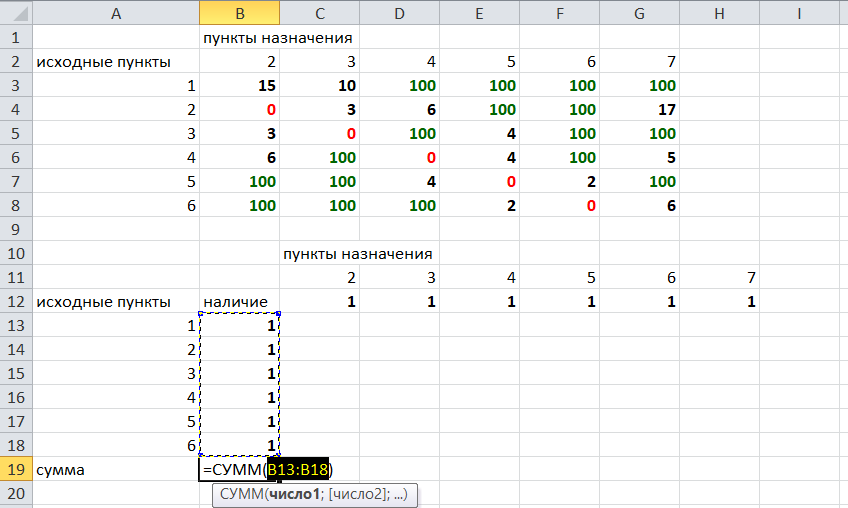 Получим в ячейке В20 число 6. Найдем суммы столбцов для пунктов назначения 2,3,..7, протянув ячейку В20: 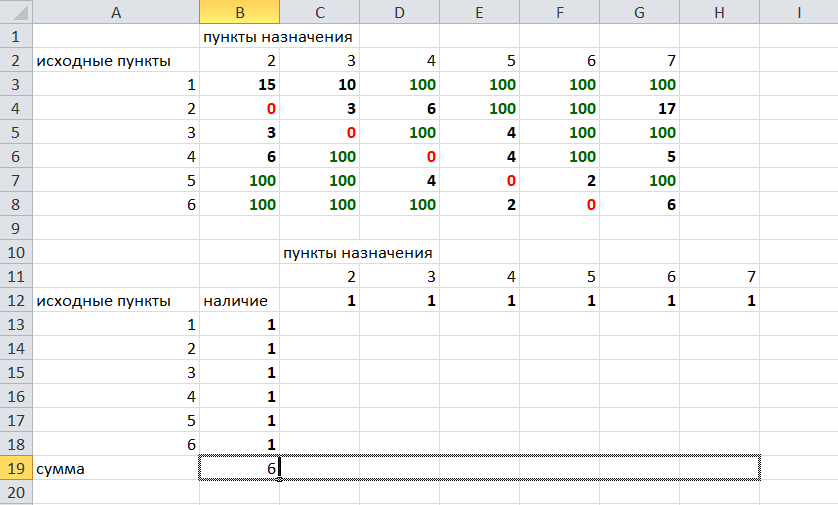 Получим:  Теперь найдем суммы по строкам с исходными пунктами: 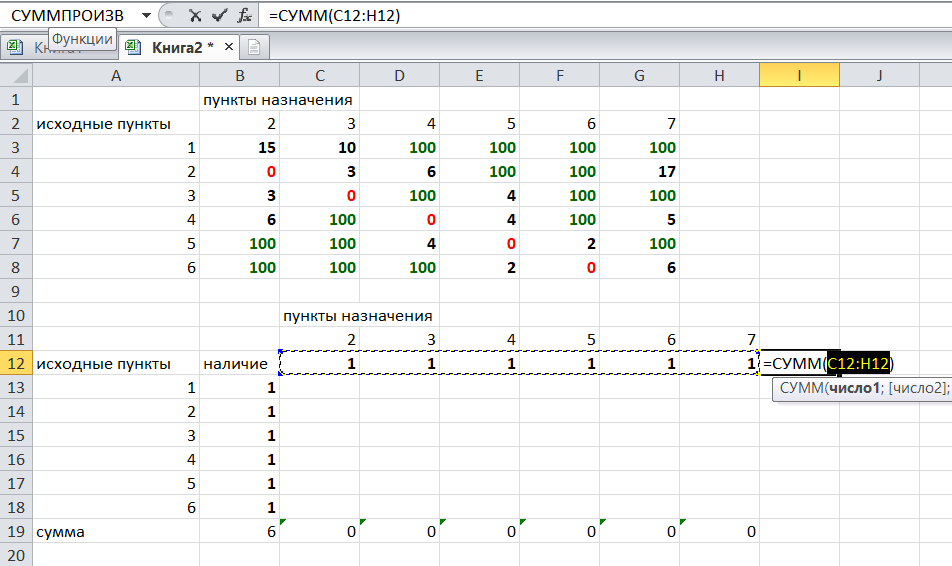 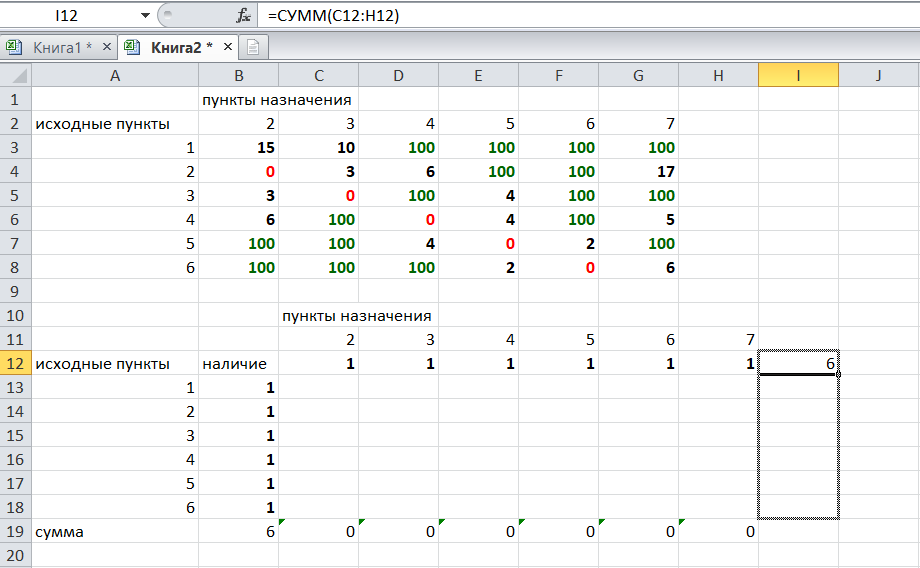 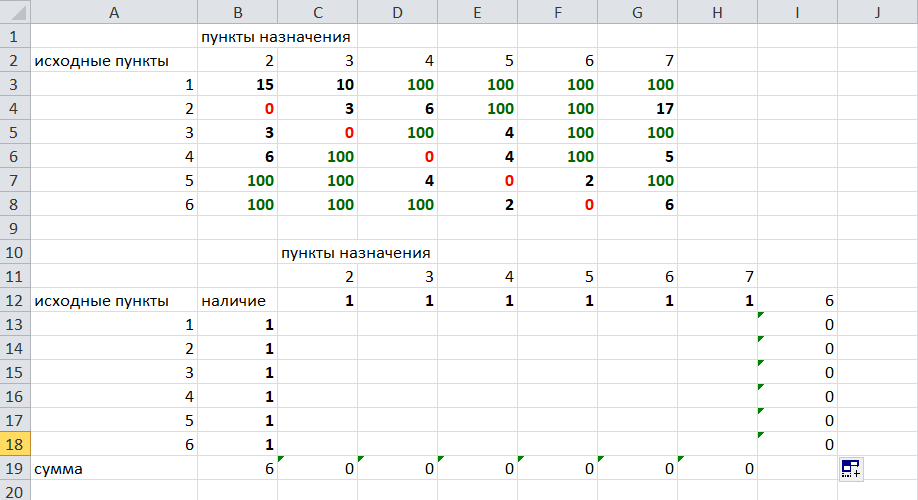 Теперь зададим формулой весь пройденный путь, это сумма произведений ячеек второй и первой таблиц. Для этого выделяем ячейку соответствующую пройденному пути, заходим на вкладку формулы, выбираем вставить функцию, находим СУММПРОИЗВ: 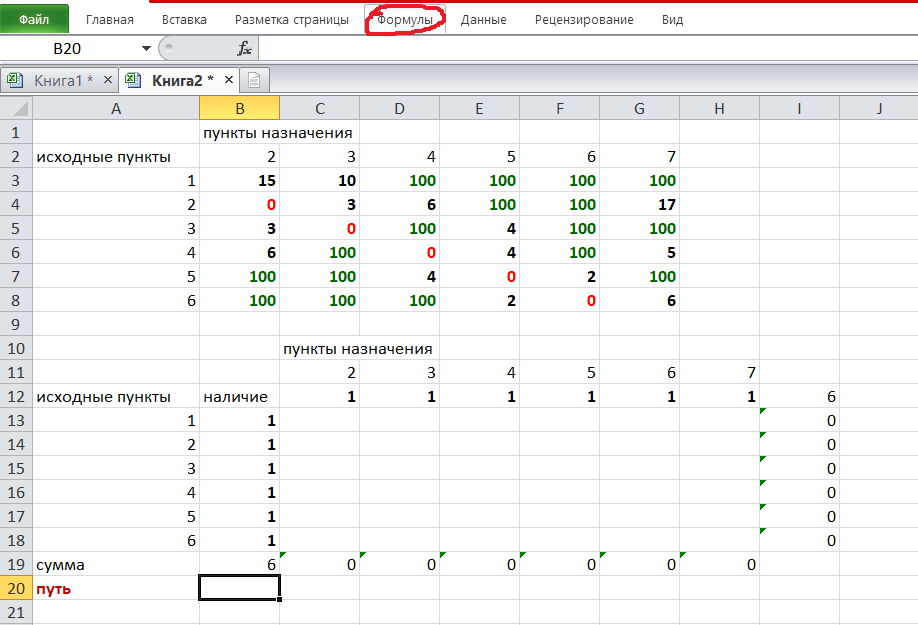 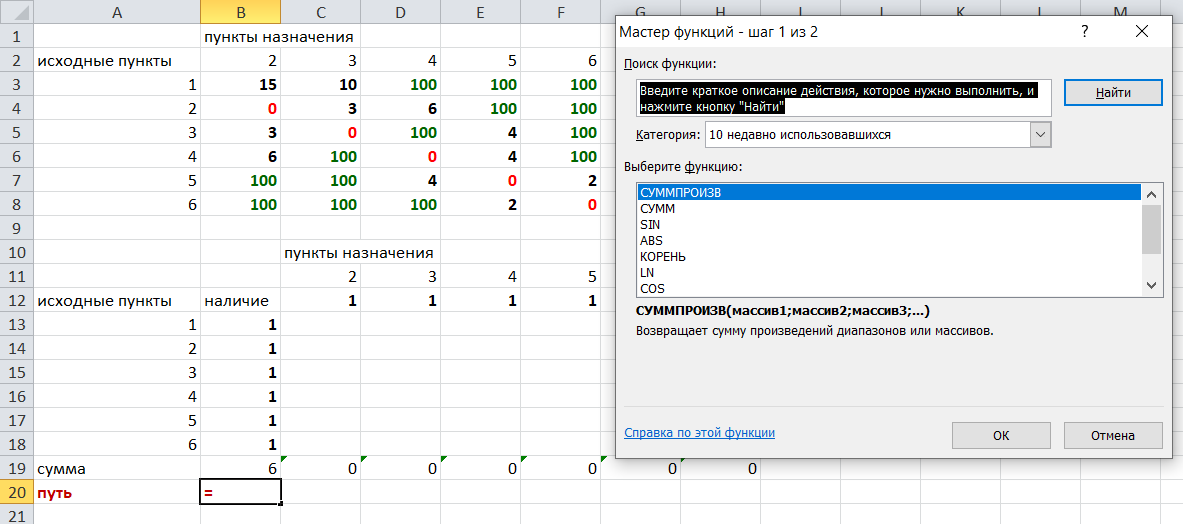 В качестве массива 1 выделяем все ячейки внутри первой таблицы: 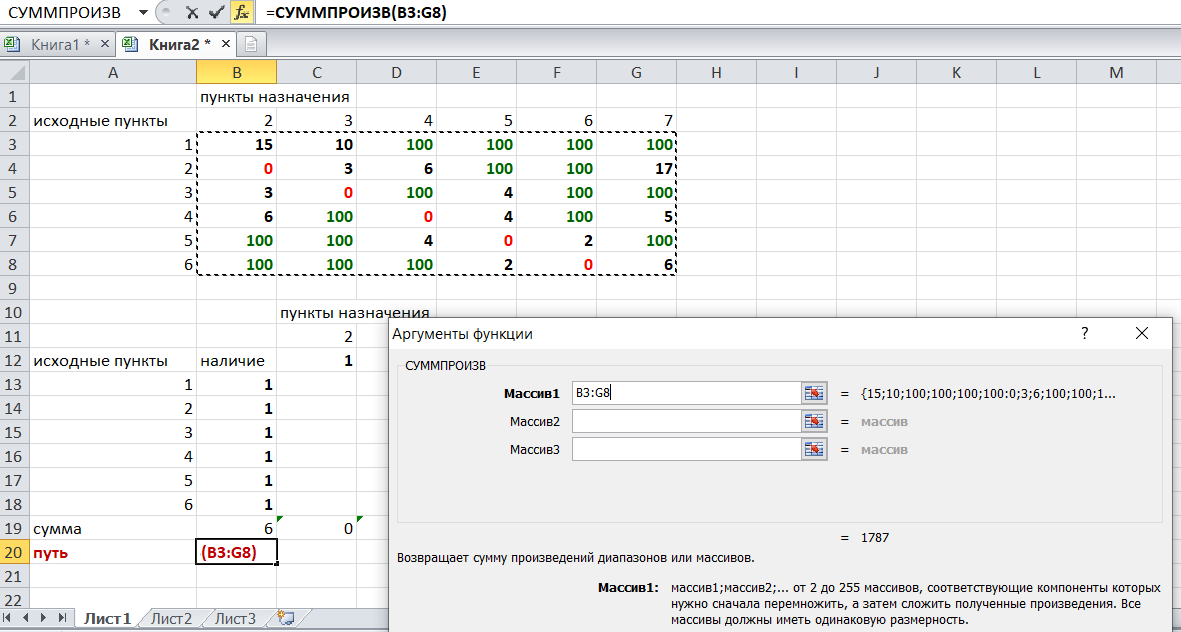 В качестве массива 2 выбираем ячейки внутри второй таблицы: 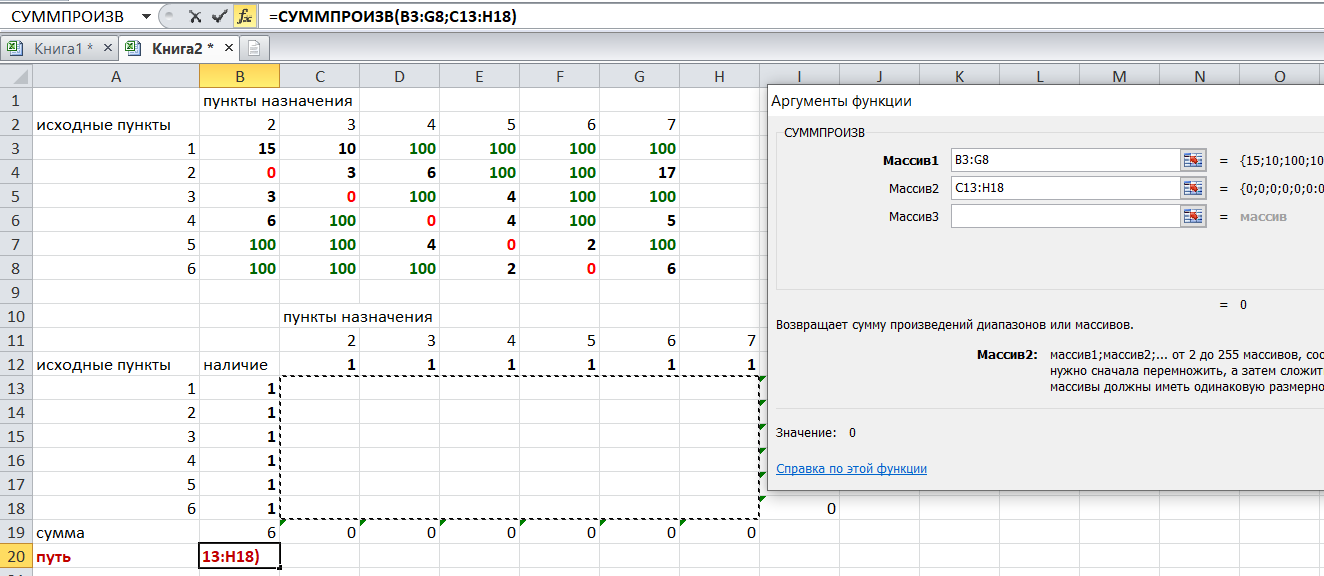 Массив 3 не заполняем. Нажимаем ОК. 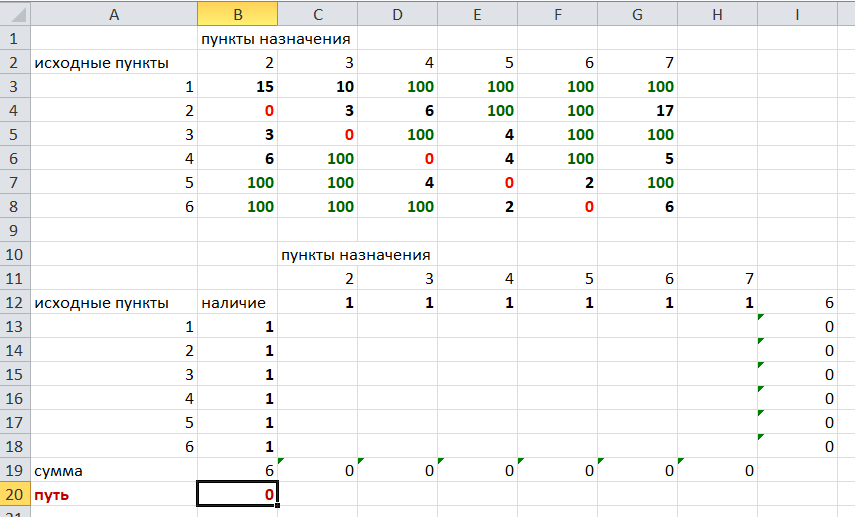 Выделяем ячейку соответствующую пройденному пути, там у нас пока записано число 0. На вкладке «данные» находим «поиск решения». Нам надо, чтобы пройденный путь был самым коротким, поэтому выбираем «оптимизировать целевую функцию» на «минимум». 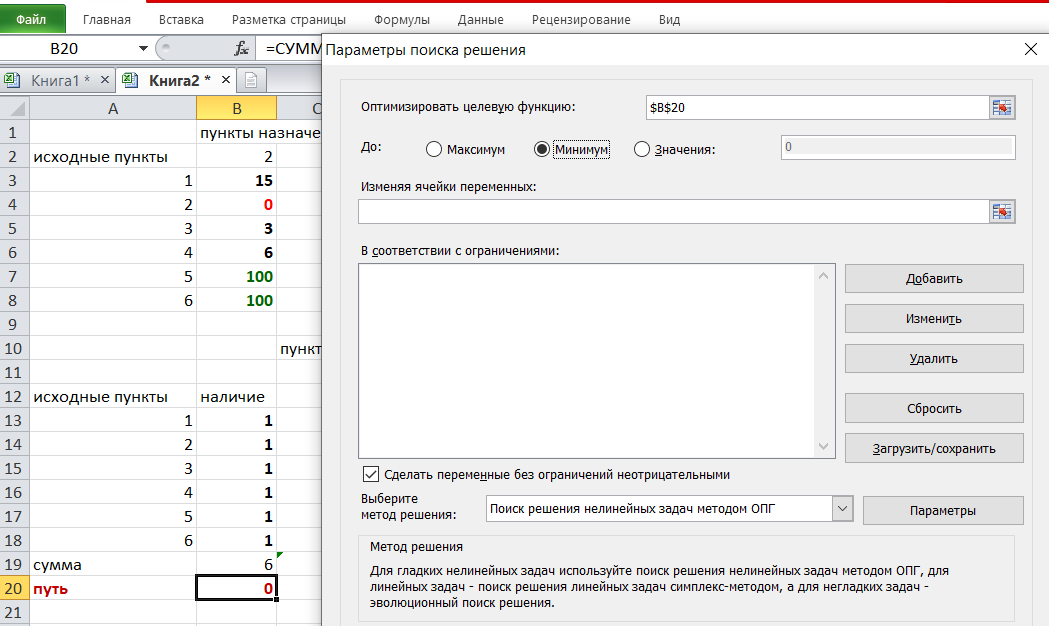 Изменять будем ячейки, стоящие внутри второй таблицы. 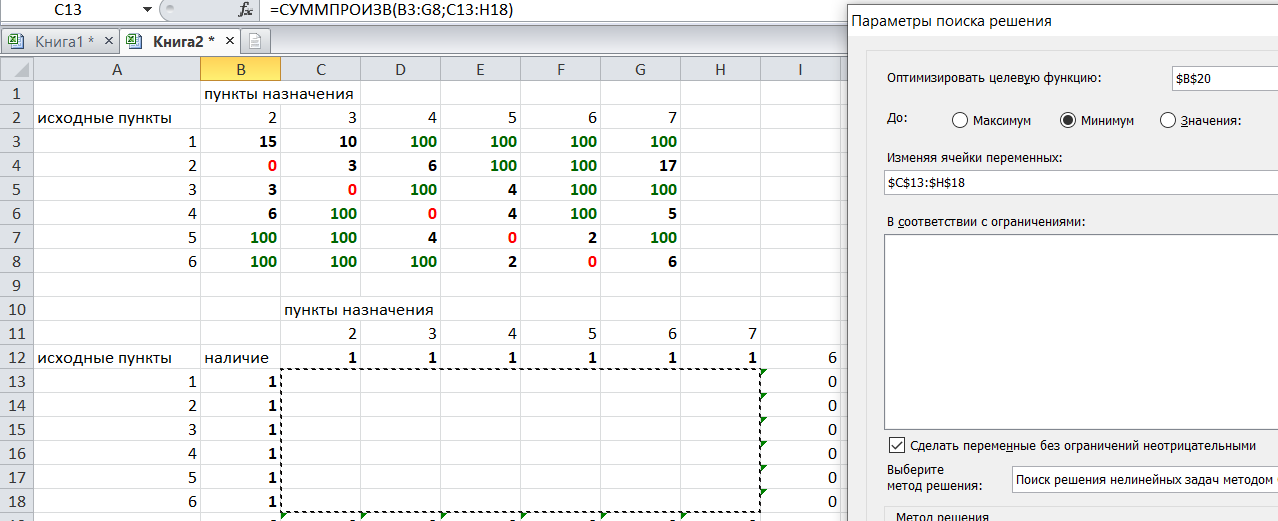 Теперь необходимо добавить ограничения. Числа стоящие внутри второй таблицы должны быть положительными. 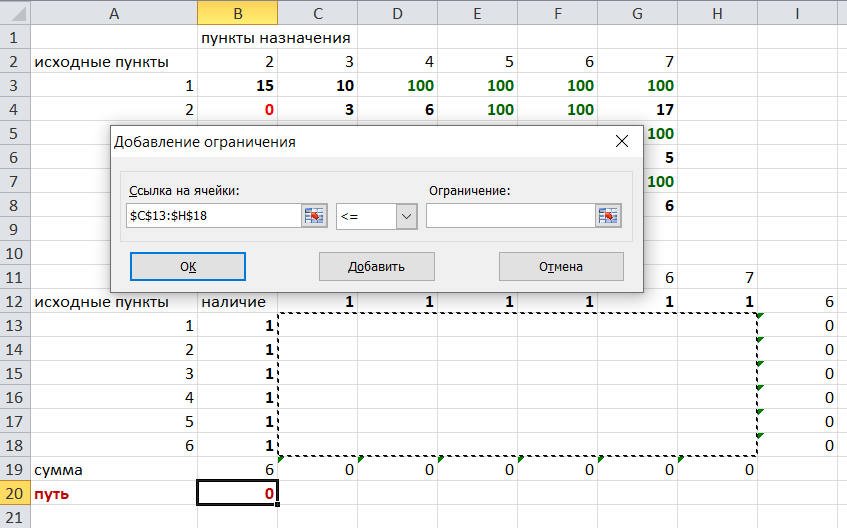 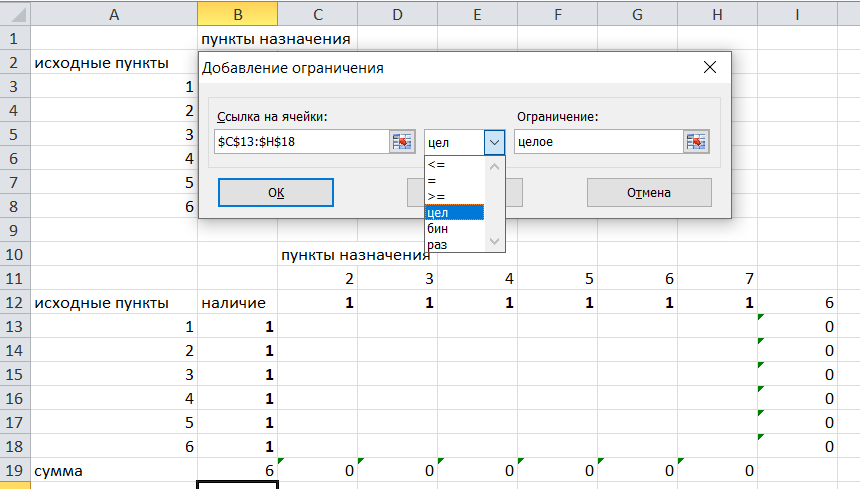 Числа внутри второй таблицы должны быть неотрицательными, добавим это ограничение: Выделяем ячейки 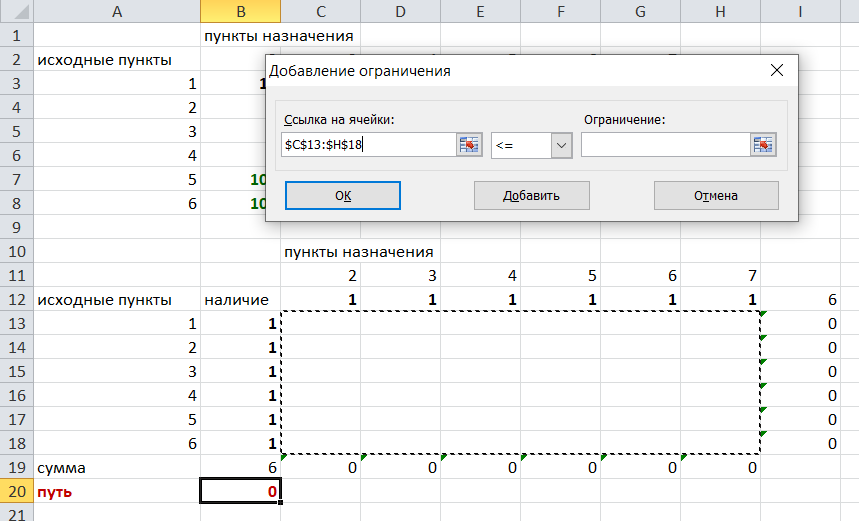 Добавляем условие неотрицательности: 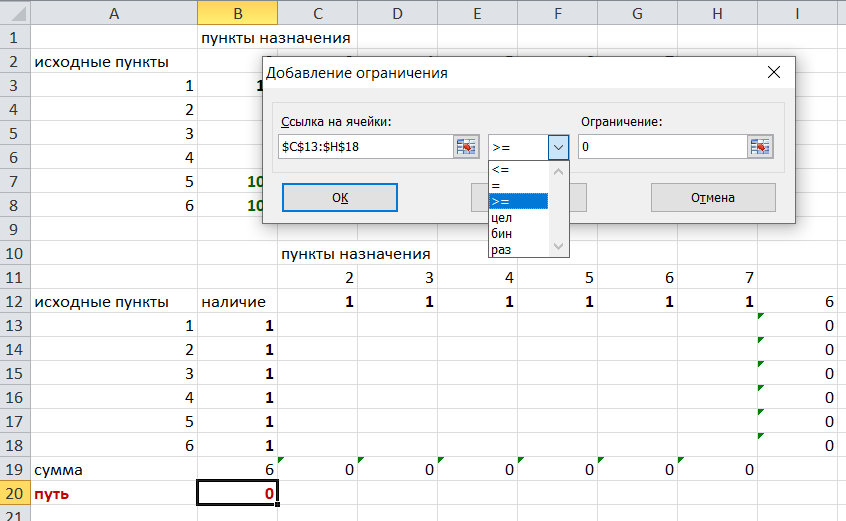 Суммы по столбцам внутри второй таблице должны быть равны 1. Это условие будет означать, что выйдя из какой-то вершины, мы можем попасть только в одну вершину, а не в 2 или 3 вершины сразу. То есть должны быть равны значения в выделенных ячейках: 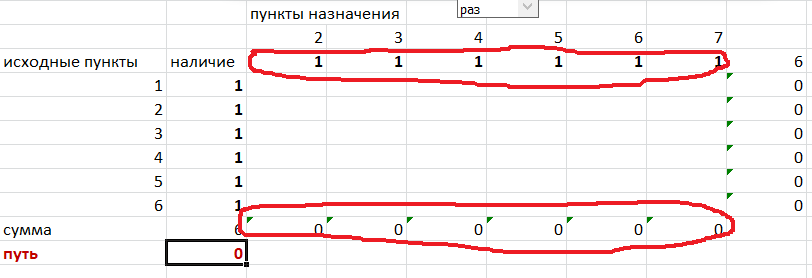 Добавим это ограничение: 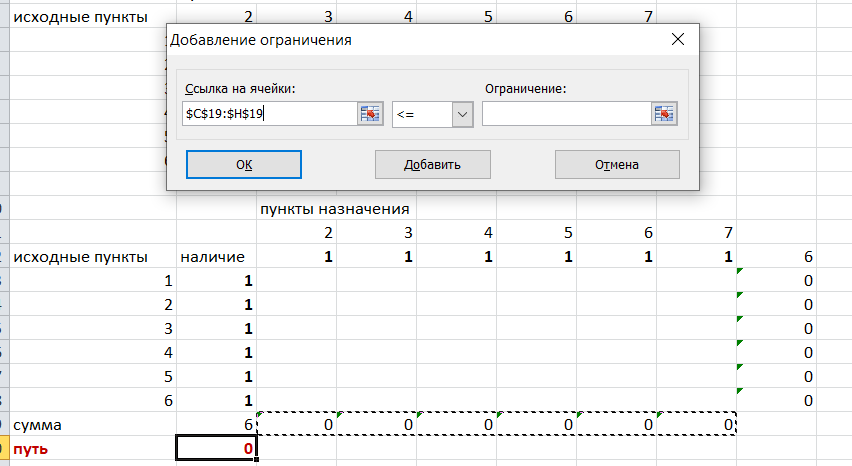 В качестве ограничения выбираем ячейки с 1: 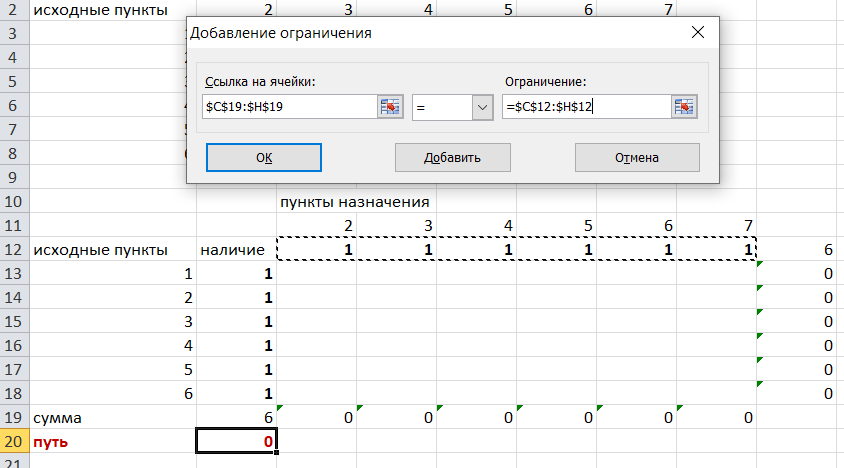 И добавим последнее ограничение. Суммы по строкам должны быть равны 1. То есть движение может идти только из одной вершины в одну. Нам надо добавить равенство значений в выделенных ячейках:  Добавим это ограничение: 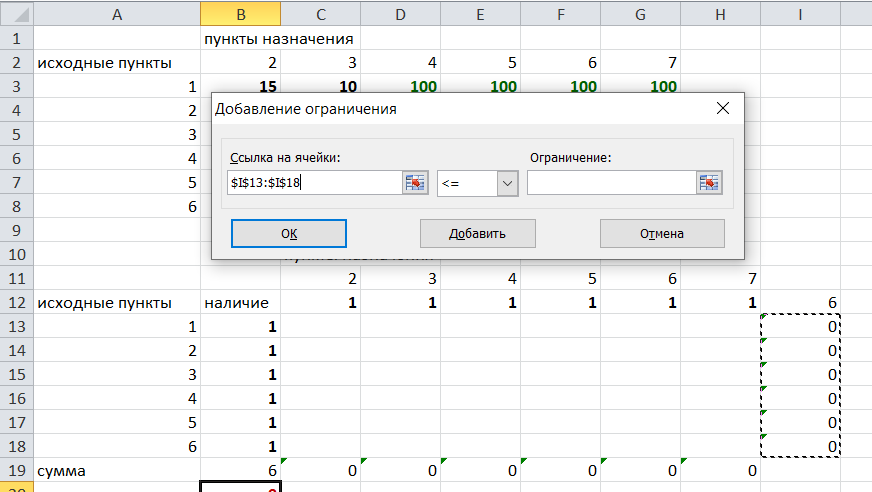 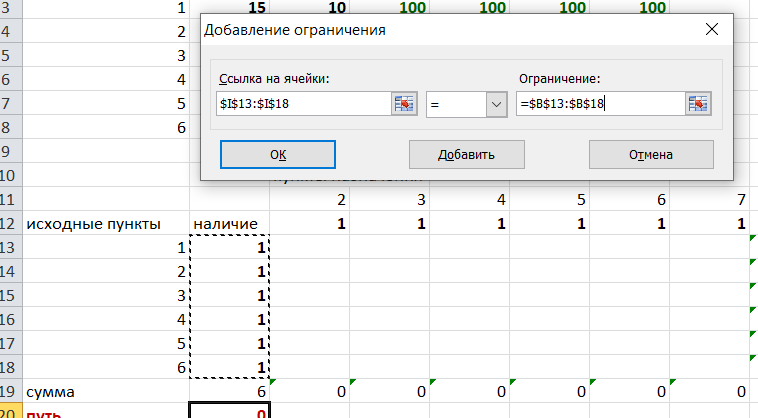 Нажимаем ОК. Выбираем Поиск решения линейных задач симплекс-методом. Находим решение. 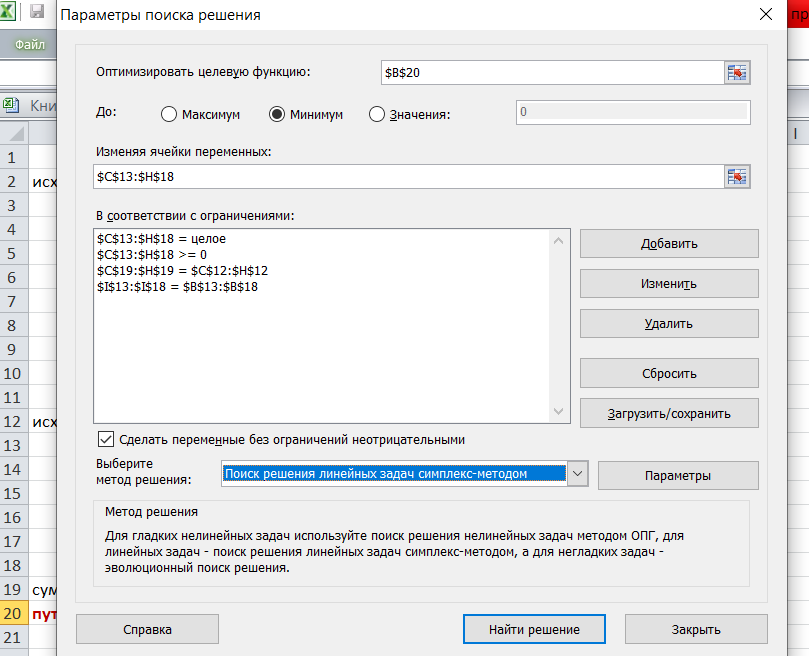 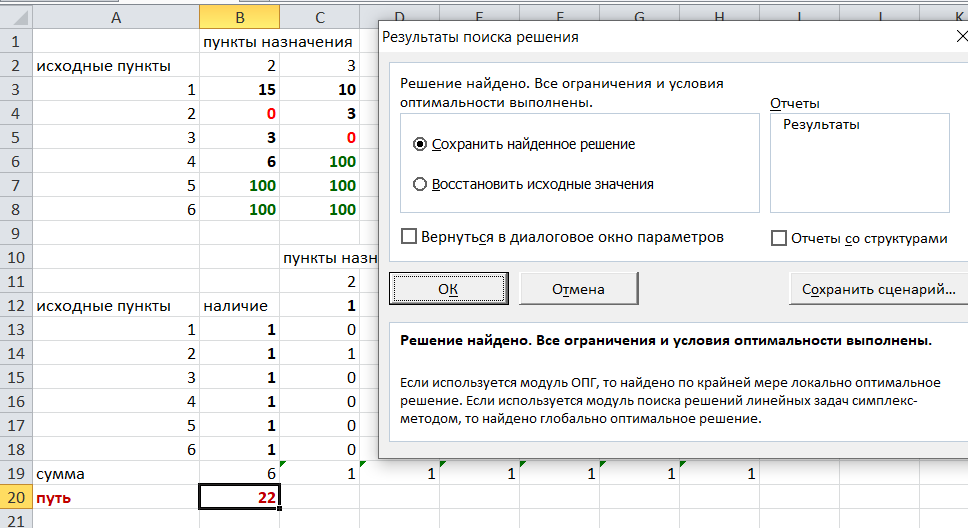 Нажимаем ОК. Получившееся решение: 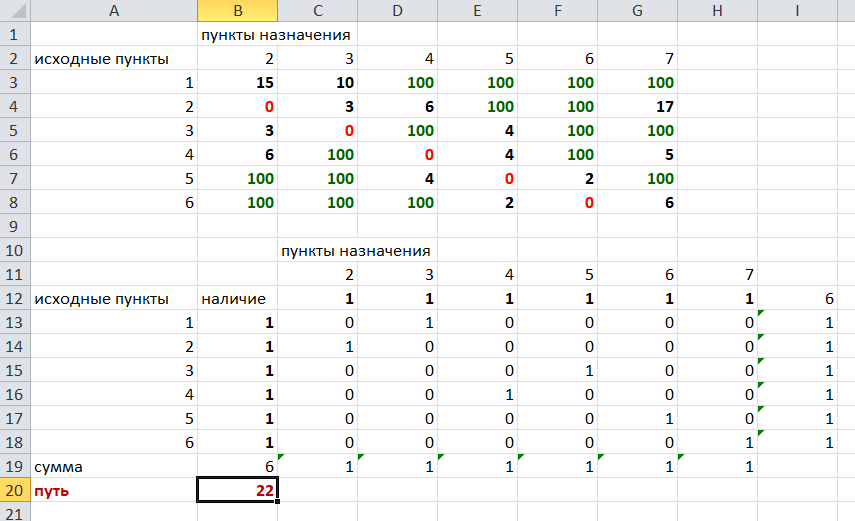 Их второй таблицы мы видим, что кратчайший путь из вершины 1 в вершину 7 составит 22. Давайте посмотрим, по каким вершинам он пройдет. 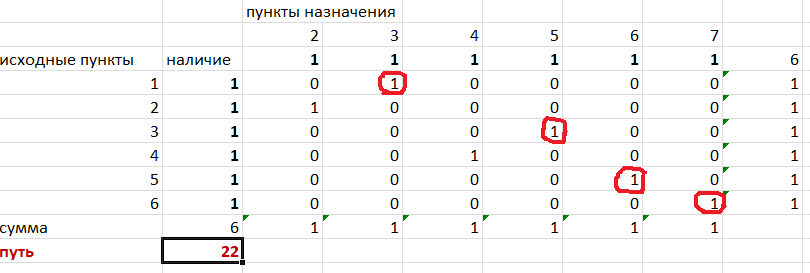 Из первой строки мы находим, что 1 стоит только в столбце «пункт назначения3». Все остальные ячейки 0. Это значит, что из первой вершины движение по кратчайшему пути идет только в вершину 3. Поэтому далее мы должны сразу перейти в строку «исходные пункты3». В этой строке 1 стоит в «пункте назначения 5». Значит из вершины 3 переходим в вершину 5. По оставшимся строкам видим, что движение идет в вершину 6 и 7. Таким образом кратчайший путь 1-3-5-6-7 и составляет он 22 (условные единицы, если исходные расстояния были даны в км, значит 22 км). Ответ: путь 1-3-5-6-7 – кратчайший. Его длина 22. Решите предложенную задачу по описанному алгоритму в Excel. Полученное решение высылайте на эл. почту. |
