моделирование. Задачи. В узел в мы можем попасть только из узлов 1 или 7

• Название: В узел в мы можем попасть только из узлов 1 или 7
• Анкор: моделирование
• Дата: 28.04.2022
• Размер: 144.82 Kb.
• Имя файла: Задачи.docx
• Тип: Задача; #503111

Задача 1.

Требуется проложить трубопровод на дачном массиве между двумя пунктами А и В таким образом, чтобы затраты на проведение работ (в тыс. р.) были минимальные.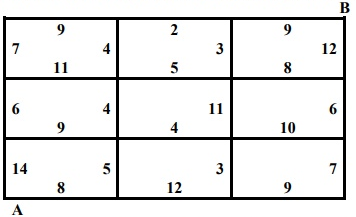


Процедуру условной оптимизации будем разворачивать в обратном направлении — от конца к началу.

Прежде всего произведем условную оптимизацию последнего, шага. Рассмотрим отдельно правый верхний угол нашей прямоугольной сетки.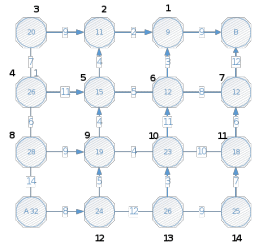


В узел В мы можем попасть только из узлов 1 или 7.

Если мы находимся в узле 1, у нас нет выбора (управление вынужденное): надо идти направо, и это обойдется нам в 9 единиц. Запишем это число 9 в кружке узла 1, а оптимальное управление покажем стрелкой, исходящей из 1 и направленной вправо.

Для узла 7 управление тоже вынужденное (вверх), расход до конца равен 12, мы его запишем в кружке узла 7. Таким образом, условная оптимизация последнего шага сделана, и условный оптимальный выигрыш для каждого из узлов 1 и 7 найден и записан в соответствующем кружке.

В узел 1 можно попасть из узлов 2 или 6.

Если мы находимся в узле 2, у нас нет выбора (управление вынужденное): надо идти направо, и это обойдется нам в 11 (9+2) единиц.

Если мы находимся в узле 6, из него можно идти вверх и вправо. Минимальное из 9+3=12 и 12+8=20 запишем узел 6.

Если мы находимся в узле 11, у нас нет выбора (управление вынужденное): надо идти вверх, и это обойдется нам в 18 (12+6) единиц.

И так далее. В итоге: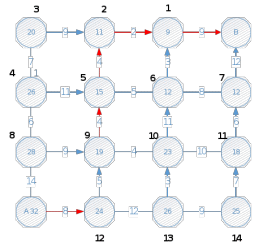



Кратчайший путь А-12-9-5-2-1-В

Стоимость = 32 д.е.

Задача 2.

Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции.

Инвестиции,	Прирост выпуска продукции, млн. р.
млн. р.	Предприятие 1	Предприятие 2	Предприятие 3	Предприятие 4
50	14	11	15	13
100	32	30	33	32
150	39	39	42	37
200	44	45	47	44
250	50	52	55	52

Занесем исходные данные в таблицу

f1	f2	f3	f4	xi
0	0	0	0	0
14	11	15	13	50
32	30	33	32	100
39	39	42	37	150
44	45	47	44	200
59	52	55	52	250

Условная оптимизация.

1-ый шаг. k = 4.

Допустим, что все средства в количестве x₄ = 250 отданы предприятию 4. В этом случае, максимальный доход, как это видно из таблицы, составит f₄(u₄) = 52, следовательно, F₄(e₄) = f₄(u₄)

e3	u4	e4 = e3 - u4	f4(u4)	F*4(e4)	u4(e4)
50	0	50	0
	50	0	13	13	50
100	0	100	0
	50	50	13
	100	0	32	32	100
150	0	150	0
	50	100	13
	100	50	32
	150	0	37	37	150
200	0	200	0
	50	150	13
	100	100	32
	150	50	37
	200	0	44	44	200
250	0	250	0
	50	200	13
	100	150	32
	150	100	37
	200	50	44
	250	0	52	52	250

2-ый шаг. k = 3.

Определяем оптимальную стратегию при распределении денежных средств между предприятиями 3, 4. При этом рекуррентное соотношение Беллмана имеет вид: F₃(e₃) = max(x₃ ≤ e₃)(f₃(u₃) + F₄(e₃-u₃))

e2	u3	e3 = e2 - u3	f3(u3)	F*3(e2)	F2(u3,e2)	F*3(e3)	u3(e3)
50	0	50	0	13	13
	50	0	15	0	15	15	50
100	0	100	0	32	32
	50	50	15	13	28
	100	0	33	0	33	33	100
150	0	150	0	37	37
	50	100	15	32	47	47	50
	100	50	33	13	46
	150	0	42	0	42
200	0	200	0	44	44
	50	150	15	37	52
	100	100	33	32	65	65	100
	150	50	42	13	55
	200	0	47	0	47
250	0	250	0	52	52
	50	200	15	44	59
	100	150	33	37	70
	150	100	42	32	74	74	150
	200	50	47	13	60
	250	0	55	0	55

3-ый шаг. k = 2.

Определяем оптимальную стратегию при распределении денежных средств между предприятиями 2, 3, 4. При этом рекуррентное соотношение Беллмана имеет вид: F₂(e₂) = max(x₂ ≤ e₂)(f₂(u₂) + F₃(e₂-u₂))

e1	u2	e2 = e1 - u2	f2(u2)	F*2(e1)	F1(u2,e1)	F*2(e2)	u2(e2)
50	0	50	0	15	15	15	0
	50	0	11	0	11
100	0	100	0	33	33	33	0
	50	50	11	15	26
	100	0	30	0	30
150	0	150	0	47	47	47	0
	50	100	11	33	44
	100	50	30	15	45
	150	0	39	0	39
200	0	200	0	65	65	65	0
	50	150	11	47	58
	100	100	30	33	63
	150	50	39	15	54
	200	0	45	0	45
250	0	250	0	74	74
	50	200	11	65	76
	100	150	30	47	77	77	100
	150	100	39	33	72
	200	50	45	15	60
	250	0	52	0	52

4-ый шаг. k = 1.

Определяем оптимальную стратегию при распределении денежных средств между предприятиями 1, 2, 3, 4. При этом рекуррентное соотношение Беллмана имеет вид: F₁(e₁) = max(x₁ ≤ e₁)(f₁(u₁) + F₂(e₁-u₁))

e0	u1	e1 = e0 - u1	f1(u1)	F*1(e0)	F0(u1,e0)	F*1(e1)	u1(e1)
50	0	50	0	15	15	15	0
	50	0	14	0	14
100	0	100	0	33	33	33	0
	50	50	14	15	29
	100	0	32	0	32
150	0	150	0	47	47	47	0
	50	100	14	33	47
	100	50	32	15	47
	150	0	39	0	39
200	0	200	0	65	65	65	0
	50	150	14	47	61
	100	100	32	33	65
	150	50	39	15	54
	200	0	44	0	44
250	0	250	0	77	77
	50	200	14	65	79	79	50
	100	150	32	47	79
	150	100	39	33	72
	200	50	44	15	59
	250	0	59	0	59

Поясним содержимое таблиц и последовательность проведения расчетов.

Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 4-го шага столбцы 5 и 6 отсутствуют).

В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.

Безусловная оптимизация.

Из таблицы 4-го шага имеем F*₁(e⁰ = 250) = 79. То есть максимальный доход всей системы при количестве средств e⁰ = 250 равен 79

Из этой же таблицы получаем, что 1-му предприятию следует выделить u*₁(e⁰ = 250) = 50

При этом остаток средств составит:

e¹ = e⁰ - u¹ = 250 - 50 = 200

Из таблицы 3-го шага имеем F*₂(e¹ = 200) = 65. То есть максимальный доход всей системы при количестве средств e¹ = 200 равен 65

Из этой же таблицы получаем, что 2-му предприятию следует выделить u*₂(e¹ = 200) = 0

При этом остаток средств составит:

e² = e¹ - u² = 200 - 0 = 200

Из таблицы 2-го шага имеем F*₃(e² = 200) = 65. То есть максимальный доход всей системы при количестве средств e² = 200 равен 65

Из этой же таблицы получаем, что 3-му предприятию следует выделить u*₃(e² = 200) = 100

При этом остаток средств составит:

e³ = e² - u³ = 200 - 100 = 100

Последнему предприятию достается 100

Итак, инвестиции в размере 250 необходимо распределить следующим образом:

1-му предприятию выделить 50

2-му предприятию выделить 0

3-му предприятию выделить 100

4-му предприятию выделить 100

Что обеспечит максимальный доход, равный 79