Решение. Решение Задача 2 Условие задачи
 Скачать 240.5 Kb. Скачать 240.5 Kb.
|
|
Задача 1 Условие задачи: Кольцо из медного провода массой m=10 г помещено в однородное магнитное поле (B=0,5 Тл) так, что плоскость кольца составляет угол β=60° с линиями магнитной индукции. Определить заряд Q, который пройдет по кольцу, если снять магнитное поле. Решение:  Задача 2 Условие задачи: Альфа-частица, имеющая скорость v=2 Мм/с, влетает под углом α=30° к сонаправленному магнитному (В=1 мТл) и электрическому (Е=1 кВ/м) полям. Определить ускорение a* альфа-частицы. *Ускорение a определяется в момент вхождения заряженной частицы в область пространства, где локализованы однородные магнитное и электрическое поля. Решение:  Задача 3 Условие задачи: За время t=8 с при равномерно возраставшей силе тока в проводнике сопротивлением R=8 Ом выделилось количество теплоты Q=500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю. Решение: 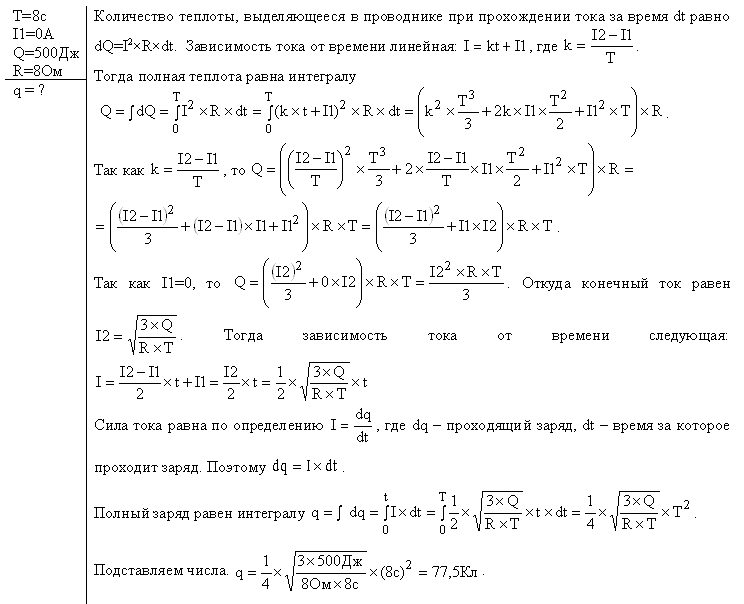 Задача 4 Условие задачи: Диск радиусом R=8 см несет равномерно распределенный по поверхности заряд (σ=100 нКл/м2). Определить магнитный момент pm, обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска. Угловая скорость вращения диска ω=60 рад/с. Решение: 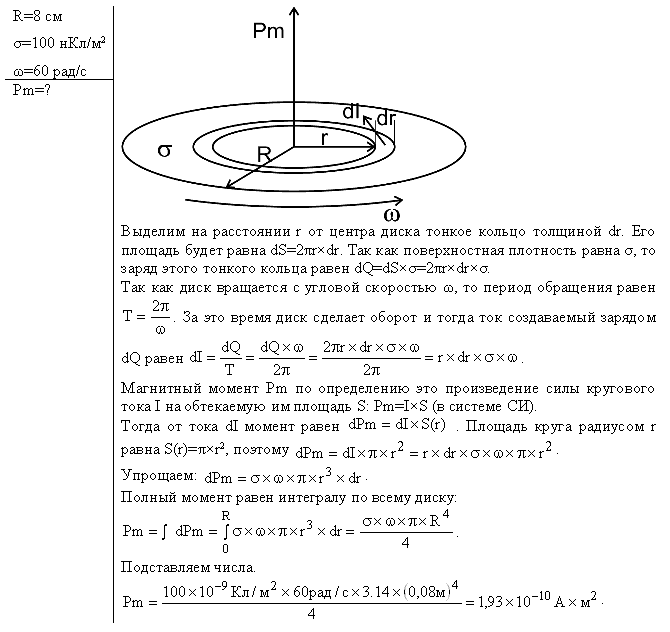 Задача 5  Задача 6 Условие задачи: На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2 (рис. 24). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1=4σ, σ2=σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ=30 нКл/м2, r=l,5R; 3) построить график E(r). Решение:  Задача 7 Условие задачи: В однородное электрическое поле напряженностью Е=200 В/м влетает (вдоль силовой линии) электрон со скоростью v0=2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной. Решение:  Задача 8 Пластины плоского конденсатора площадью S = 0,01 м2 каждая притягиваются друг к другу с силой F = 30 мН. Пространство между пластинами заполнено слюдой. Найти заряды q, находящиеся на пластинах, напряженность Е поля между пластинами и объемную плотность энергии W0 поля. Решение:  Задача 9 В простейшей модели атома водорода считается, что электрон движется вокруг неподвижного протона по окружности радиусом 5*10 в -10 м. Какие в этой модели скорость электрона и частота его вращения? Решение: ma=F=k* qQ/R^2 a=k/m*qQ/R^2 a=Rw^2 w=(k/m*qQ/R^3)^(1/2) U=w/2Pi=(k/m*qQ/R^3)^(1/2)/2Pi - частота вращения v=Rw=(k/m*qQ/R)^(1/2) – скорость ^- знак степени: ^(1/2) - корень квадратный ^2- квадрат k -коэффициент, в системе си равне 1/4PiE0, в СГС - 1 |
