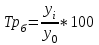Судебная статистика. Решение задачи. Индекс физического объема преступлений против собственности равен

• Название: Решение задачи. Индекс физического объема преступлений против собственности равен
• Анкор: Судебная статистика
• Дата: 05.05.2022
• Размер: 43.51 Kb.
• Имя файла: Судебная статистика.docx
• Тип: Решение; #513096

1. Задача 1

В первом полугодии 2012 г. в районном отделе внутренних дел г. М. было зарегистрировано следующее количество преступлений против собственности: 200 краж стоимостью 3000 р., 26 грабежей стоимостью 13 000 р., 5 разбоев стоимостью 7000 р.

В первом полугодии 2013 г. в этом же райотделе было зарегистрировано следующее количество преступлений против собственности: 215 краж стоимостью 3500 р., 15 грабежей стоимостью 10 000 р., 7 разбоев стоимостью 12 000 р. Определите индекс физического объема преступлений против собственности.
Решение задачи.

Индекс физического объема преступлений против собственности равен:

I_ф = (215 ∙ 3500 + 15 ∙ 10000 + 7 ∙ 12000) / (200 ∙ 3000 + 26 ∙ 13000

+ 5 ∙ 7000) = (752500 + 150000 + 84000) / (600000 + 338000 + 35000) =

= 986500 / 973000 = 1,014 или 101,4%.
Ответ: Индекс физического объема преступлений против собственности равен 1,014 или 101,4%.

2. Задача № 2-3

Дано два ряда чисел:

1) 2, 4, 8, 9, 11, 4;

2) от 0 до 3, от 3 до 5, от 6 до 8, от 8 до 10, от 11 до 12, от 0 до 15.
Вычислите среднее квадратическое отклонение и коэффициент вариации этих рядов и определите ряд менее количественно неоднородный.
Решение задач.

Находим среднюю арифметическую первого ряда:

Х1 = (2 + 4 + 8 + 9 + 11 + 4) / 6 = 38 / 6 = 6,33

Находим дисперсию первого ряда:

D1 = [(2 – 6,33)² + (4 – 6,33)² + (8 – 6,33)² + (9 – 6,33)² + (11 – 6,33)² + (4 – 6,33)²] / 6 = (18,7489 + 5,4289 + 2,7889 + 7,1289 + 21,8089 + +5,4289) / 6 = 10,222

Находим среднее квадратическое отклонение первого ряда, извлекая квадратный корень из дисперсии:

М1 = 3,197

Находим коэффициент вариации первого ряда:

V1 = M1 / X1 ∙ 100% = 3,197 / 6,33 ∙ 100% = 50,5%

Заменим второй ряд средними интервальными значениями:

1,5, 4, 7, 9, 11,5, 7,5

Находим среднюю арифметическую второго ряда:

Х2 = (1,5 + 4 + 7 + 9 + 11,5 + 7,5) / 6 = 40,5 / 6 = 6,75

Находим дисперсию второго ряда:

D2 = [(1,5 – 6,75)² + (4 – 6,75)² + (7 – 6,75)² + (9 – 6,75)² + (11,5 – 6,75)² + (7,5 – 6,75)²] / 6 = (27,5625 + 7,5625 + 0,0625 + 5,0625 + 22,5625 + +0,5625) / 6 = 10,5625

Находим среднее квадратическое отклонение второго ряда, извлекая квадратный корень из дисперсии:

М2 = 3,25

Находим коэффициент вариации первого ряда:

V2 = M2 / X2 ∙ 100% = 3,25 / 6,75 ∙ 100% = 48,1%

Так как V1 > V2, то первый ряд менее количественно неоднородный.

3. Задача 4

В районном отделе внутренних дел работают 7 следователей, которые расследуют уголовные дела в следующие сроки: один следователь расследует одно уголовное дело в срок от 15 суток до 30 суток; три следователя расследуют по одному уголовному делу в срок от 23 суток до 30 суток; два следователя расследуют по одному уголовному делу в срок от 28 суток до 45 суток; один следователь расследует одно уголовное дело в срок от 2 суток до 2 месяцев. Определите средний срок расследования уголовного дела в указанном районном отделе МВД.
Решение задачи.

Находим средние сроки расследования:

а) для следователя, который расследует одно уголовное дело в срок от 15 суток до 30 суток:

X1 = (15 + 30) / 2 = 22,5 дней.

б) для трех следователей, которые расследуют по одному уголовному делу в срок от 23 суток до 30 суток:

X2 = (23 + 30) / 2 = 26,5 дней.

в) для двух следователей, которые расследуют по одному уголовному делу в срок от 23 суток до 30 суток:

X3 = (28 + 45) / 2 = 36,5 дней.

г) для следователя, которые расследуют по одному уголовному делу в срок от 2 суток до двух месяцев:

X4 = (2 + 60) / 2 = 31 дней.

Тогда средний срок расследования уголовного дела в указанном районном отделе МВД будет равен:

Х = (22,5 ∙ 1 + 26,5 ∙ 3 + 36,5 ∙ 2 + 31 ∙ 1) / 7 = (22,5 + 79,5 + 73 + 31) / 7 = 29,4 дней.

Ответ: 29,4 дней.
4. Задача 5

В г. Ш за 12 месяцев 2009 г. было зарегистрировано следующее количество преступлений:

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь	Июль	Август	Сентябрь	Октябрь	Ноябрь	Декабрь
Всего	215	230	243	237	245	251	249	306	309	312	321	333

Исходя из этих данных, определите средний темп прироста преступности за указанный период в г. Ш.
Решение задачи.

Методы расчета показателей динамики представлены в таблице:

Наименование показателя	Метод расчета
	Цепные (с переменной базой сравнения)	Базисные (с постоянной базой сравнения)
1. Абсолютный прирост
2. Темп роста
3. Темп прироста

Применяя указанные формулы, рассчитаем показатели динамики преступности в г. Ш и запишем их в расчетную таблицу

Показатели	Базисный месяц	Месяцы анализируемого периода
		2	3	4	5	6	7	8	9	10	11	12
Количество преступлений	215	230	243	237	245	251	249	306	309	312	321	333
Базисные темпы роста, %	100	107	113	110	114	117	116	142	144	145	149	155
Базисные темпы прироста, %		7	13	10	14	17	16	42	44	45	49	55
Базисные аб-солютные приросты		15	28	22	30	36	34	91	94	97	108	118
Цепные темпы роста, %		107	106	98	103	102	99	123	101	101	103	104
Цепные темпы прироста, %		7	-1	-8	5	-1	-3	24	-22	0	2	1
Цепные абсолютные приросты		15	13	-6	8	6	-2	57	3	3	9	12

Среднемесячное количество преступлений для интервального ряда вычисляем по формуле средней арифметической простой:

, где y_i - сумма уровней ряда, n – их число.

_

у = (215 + 230 + 243 + 237 + 245 + 251 + 249 + 306 + 309 + 312 + 321 +

+ 333) / 12 = 271

Находим среднемесячный темп роста, который служит сводной обобщающей характеристикой изменения уровня динамического ряда. Он исчисляется по формуле средней геометрической: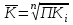

где Кi - цепные коэффициенты роста, n – число коэффициентов роста, П – символ произведения.

_

К = ( 1,107 ∙ 1,106 ∙ 0,98 ∙ 1,103 ∙ 1,102 ∙ 0,99 ∙ 1,123 ∙ 0,99 ∙ 1,123 ∙

∙ 1,101 ∙ 1,101 ∙ 1,103 ∙ 1,104)^1/11 = 2,66094^1/11 = z

lnZ = 1/11 ∙ ln 2,66094 = 0,08897

Z = e^0,08897 = 1.093 или 109,3%,

Среднегодовой темп прироста определяем как разность между среднегодовым темпом роста, выраженным в процентах, и 100%.

Тпр=109,3 – 100 = 9,3 %.

Находим средний абсолютный прирост преступлений:

, где y_ц – цепные абсолютные приросты, y_б =y_n-y₀, n – число цепных приростов.

∆y = (15 + 13 – 6 + 8 + 6 – 2 + 57 + 3 + 3 + 9) / 11 = 11

то есть в среднем за каждый месяц рассматриваемого периода количество преступлений увеличивалось в среднем на 11 или на 9,3%.

Ответ. Средний темп прироста преступности за указанный период в г. Ш. составляет 9,3%.

Список использованных источников
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики.- М.: Финансы и статистика, 2015.

2. Теория статистики: Учебник / Под ред. Шмойловой Р.А..- М.: Финансы и кредит, 2014.

3. Салин В.Н., Чурилова Э.Ю. Курс теории статистики.- М.: Финансы и статистика, 2016.

4. Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика. Учебник.- М.: Юристъ, 2017.

5. Харченко Л.Л., Долженкова В.Г. и др. Статистика: Курс лекций / Под ред. В.Г.Ионина.- Новосибирск: Изд-во НГАЭиУ, М.: ИНФРА-М, 2015.- 310 с.

6. Теория статистики: Учебник / Под ред. Громыко Г.Л..- М.: ИНФРА-М, 2015.

7. Гусаров В.М. Статистика.- М.: ЮНИТИ, 2011.

8. Статистика / Под ред. Елисеевой И.И.- М.: Проспект, 2013.