Решение задачи из раздела Статика. Решение задачи из раздела Статика
 Скачать 41.36 Kb. Скачать 41.36 Kb.
|
|
Решение задачи из раздела Статика Найти силу натяжения упругой нити, удерживающей груз в состоянии равновесия на идеально гладкой наклонной плоскости. 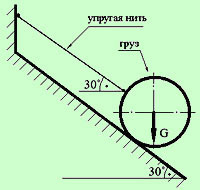 Исходные данные: Вес груза G = 100 Н, угол наклона поверхности указан на рисунке. Решение: Поскольку груз находится в равновесии, решение задачи возможно с применением методов Статики, т. е. с на основе анализа причин, по которым тело находится в неподвижном состоянии (в равновесии). Итак, сначала необходимо определить – под влиянием каких сил груз находится в состоянии равновесия. Кроме силы тяжести G, на груз наложены две связи, ограничивающие его перемещение: гибкая связь (упругая нить) и наклонная плоскость. Реакция гибкой связи Rн направлена вдоль линии этой связи (вдоль нити), а реакция плоскости Rп всегда перпендикулярна этой плоскости и приложена в точке касания телом плоскости (см. схему). Задача может быть решена двумя методами. Определив направление реакций, можно решить эту задачу графическим методом, построив силовой треугольник, который будет замкнутым, поскольку векторная сумма сил равна нулю (равновесие груза). Для построения векторной цепочки (в нашем случае – треугольник) откладываем силу тяжести груза G в определенном масштабе (поскольку нам известны и направление, и величина этой силы).  Для реакций мы знаем лишь их направление (величина сил неизвестна). От концов вектора силы G откладываем отрезки прямых, параллельные реакциям, и точка пересечения этих прямых позволит нам получить искомый треугольник сил. Теперь можно определить величину любой из реакций, измерив ее длину на чертеже линейкой и умножив на масштаб чертежа, который задает сила G. Порядок построений показан на рисунке а). Аналитическим методом эта задача решается с помощью уравнений равновесия, исходя из условия, что сумма проекций всех сил на любую координатную ось равна нулю. Разумеется, необходимо выбрать удобную систему координат, тогда для решения задачи потребуется минимальное количество уравнений. В нашем случае можно любую из координат расположить так, чтобы одна из неизвестных реакций была ей перпендикулярна, тогда проекция этой силы на данную координатную ось будет равна нулю. Поскольку нам необходимо найти силу натяжения нити (реакция Rн), то расположим координатную ось y так, чтобы реакция плоскости (Rп) была ей перпендикулярна (рис. в). Тогда реактивная сила Rп проецируется в точку, т. е. в ноль, и для решения задачи потребуется лишь сумма проекций сил G и Rн на ось y: ΣFy = 0 => Rн – G cos60˚ = 0, откуда найдем искомую реакцию Rн: Rн = G cos60˚ = 100×0,5 = 50 Н. |
