Уравнение параболического типа. Уравнения параболического типа. Решение задачи Коши Рассмотрим задачу Коши для уравнения теплопроводности,,, 5) с условием на прямой
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Разностные схемы для уравнений параболического типа 1. Решение задачи КошиРассмотрим задачу Коши для уравнения теплопроводности с условием на прямой t=0 Требуется найти функцию Будем считать, что задача (3.5), (3.6) имеет в верхней полуплоскости единственное решение 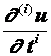 , i=1, 2 и , i=1, 2 и 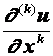 , k=1, 2, 3, 4. , k=1, 2, 3, 4.Запишем задачу (3.5), (3.6) в виде 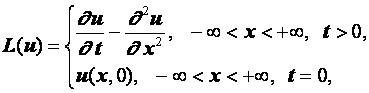 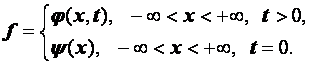 Будем далее считать, что t изменяется в пределах Г − объединение прямых t=0иt=T. Выберем прямоугольную сетку и заменим область Заменим задачу 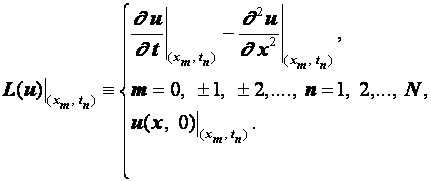 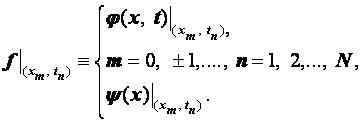 Для замены выражений 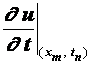 и и 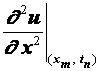 воспользуемся формулами численного дифференцирования. Имеем: воспользуемся формулами численного дифференцирования. Имеем: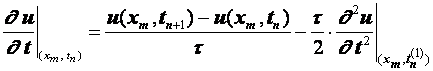 , (3.7) , (3.7)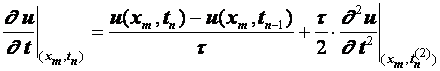 , (3.8) , (3.8)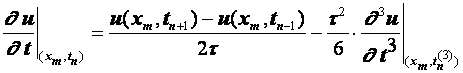 , (3.9) , (3.9)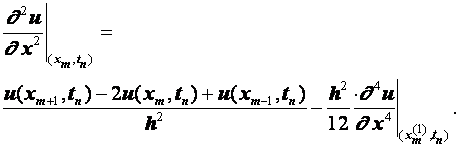 (3.10) (3.10)Назовем некоторую совокупность узлов, привлекаемых для замены задачи 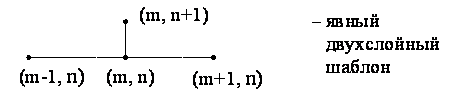 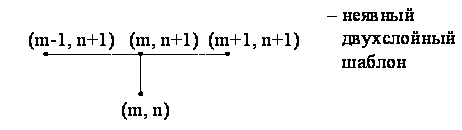 Рис. 3. Явный и неявный шаблоны Рассмотрим явный двухслойный шаблон. Для него 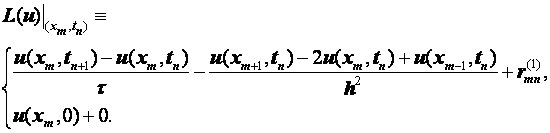 (3.11) (3.11)Здесь мы воспользовались формулами (3.7) и (3.10) и обозначили 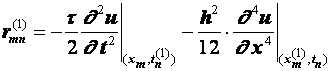 . .Введем обозначение 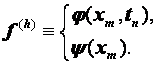 (3.12) (3.12)Теперь на основании формул (3.11), (3.12) можно записать разностную схему для задачи где разностный оператор 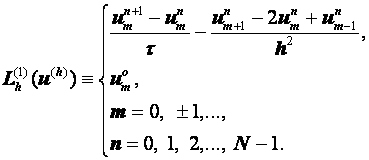 Аналогично, если использовать неявный двухслойный шаблон, можно получить такую разностную схему: где 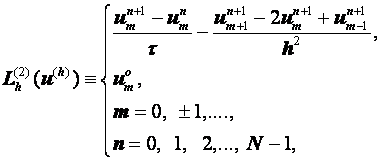 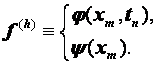 На основании формул (3.11) и (3.13) можно записать где 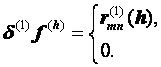 Аналогично, используя (3.11), (3.10), (3.14), получим 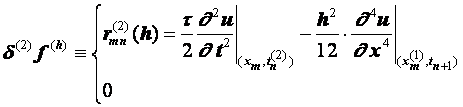 . .Выясним порядок аппроксимации разностных схем (3.13) и (3.14). В качестве 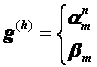 . . Норму в Пусть Предположим, что для 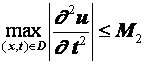 , , 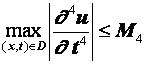 . .Тогда легко получить 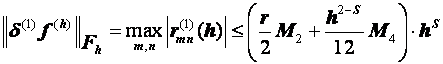 , (3.15) , (3.15)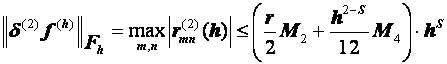 . (3.16) . (3.16)Для параболических уравнений, как мы увидим далее, в случае схемы (3.13) можно взять S=2, а в случае схемы (3.14) можно взять S=1. Из формул (3.15), (3.16) следует, что разностные схемы (3.13), (3.14) аппроксимируют задачу Разностная схема (3.13) позволяет по значениям решения на нулевом слое, то есть по значениям Разностная схема (3.14) такими свойствами не обладает. Действительно, если мы в (3.14) положим n=0, то в левой части полученной формулы будет линейная комбинация из значений 2. Устойчивость двухслойных разностных схемОпределим норму в пространстве Рассмотрим явную разностную схему (3.13). Выясним, при каких значениях r, Для доказательства устойчивости надо показать, что разностная схема однозначно разрешима и при любых 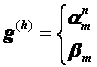 , , имеет место оценка где М – постоянная, не зависящая от Разностная схема (3.13) – явная, и поэтому ее однозначная разрешимость очевидна. Перепишем формулу Пусть выполнено условие 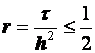 . (3.18) . (3.18)Тогда из (3.17) получим: или Неравенство (3.19) означает, что при Это свойство однородной разностной схемы принято называть принципом максимума. Положим в (3.19) Заметим, что 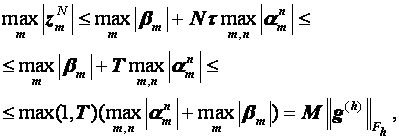 (3.20) (3.20)где обозначено 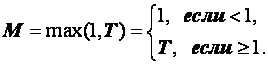 На основании (3.20) можно записать Таким образом, разностная схема (3.13) при выполнении условия (3.18), налагаемого на 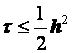 . (3.21) . (3.21)Это приводит к тому, что если мы желаем сохранить устойчивость, то при вычислениях по схеме (3.13) шаг по времени Обратимся теперь к разностной схеме (3.14), соответствующей шаблону, изображенному на рис. 4, 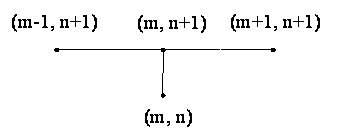 Рис. 4. Неявный двухслойный шаблон и перепишем ее в виде 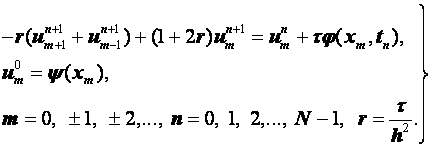 (3.22) (3.22)Посмотрим, какие надо проделать вычисления, чтобы, используя формулы (3.22), можно было вычислить, например, значения 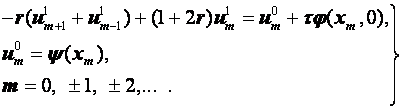 (3.23) (3.23)Формулы (3.23) представляют собой бесконечную систему линейных уравнений относительно неизвестных Решение таких систем является сложной и трудоемкой задачей, поэтому разностные схемы (3.14) неудобны для задач Коши на бесконечных отрезках и применяется редко. Однако если отрезок оси x, на котором рассматривается задача Коши, конечен, то есть Если, например, на отрезках прямых x=a и x=b, заданы условия 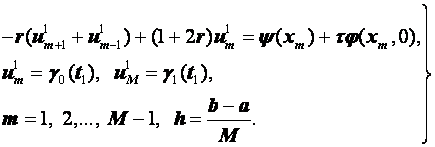 (3.24) (3.24)Формулы (3.24) представляют собой систему M+1 алгебраических уравнений относительно 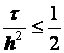 число временных слоев в случае явных схем может быть существенно большим по сравнению с числом временных слоев для неявных схем. Рассмотрим теперь вопрос о сходимости схемы (3.13). Эта схема аппроксимирует задачу (3.5), (3.6) с погрешностью порядка |
