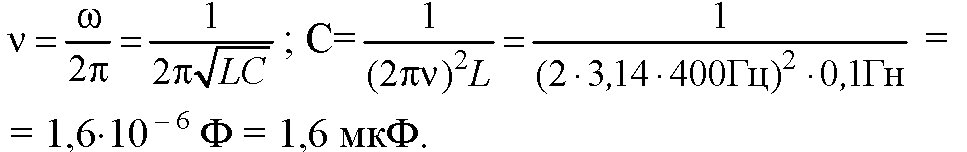Задачи на переменный ток. Решение задачи начнём с определения тока в цепи, но для этого нужно сначала определить реактивное сопротивление конденсатора
 Скачать 150.32 Kb. Скачать 150.32 Kb.
|
|
Задача 1 В сеть переменного тока включены последовательно катушка индуктивностью 3 мГн и активным сопротивлением 20 Ом и конденсатор емкостью 30 мкФ. НапряжениеUcна конденсаторе 50 В. Определите напряжение на зажимах цепи, ток в цепи, напряжение на катушке, активную и реактивную мощность. 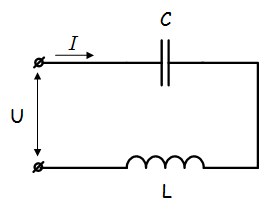 Решение задачи начнём с определения тока в цепи, но для этого нужно сначала определить реактивное сопротивление конденсатора. Как известно, реактивное сопротивление конденсатора зависит от частоты переменного тока (при её увеличении уменьшается, а при её уменьшении увеличивается), следовательно 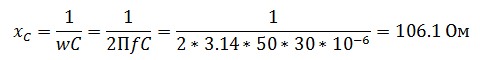 Ток в цепи находим из соображения, что элементы в цепи соединены последовательно, а значит, ток на конденсаторе и катушке будет одним и тем же. 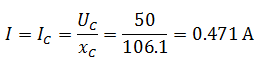 Следующим шагом мы определяем индуктивное сопротивление и напряжение катушки 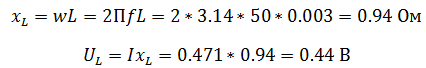 Зная активное сопротивление обмотки катушки, можем определить падение напряжения на нем Теперь, когда мы знаем напряжение на каждом из элементов, мы можем определить напряжение на зажимах цепи, которое будет равно 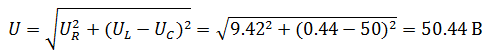 Активную мощность в данном случае можно определить как мощность, выделяемую на обмотке катушки Для определения реактивной мощности необходимо для начала определить угол сдвига ϕ 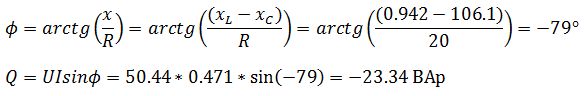 Так как реактивная мощность имеет отрицательное значение, то цепь имеет емкостной характер. Задача 2 В цепи как показано на схеме, подключены катушка, конденсатор и резисторы. Индуктивность катушки – 15 мГн, емкость конденсатора 20 мкФ,R1=10 Ом,R2=30 Ом. Напряжение источника 100 В, частота 100 Гц. Определить токи в цепи, активную, реактивную и полную мощность в цепи. 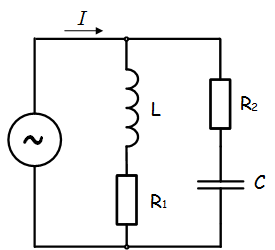 Данную задачу удобнее решать с помощью проводимостей, так как катушка и конденсатор соединены параллельно. Тогда активная проводимость первой ветви равна 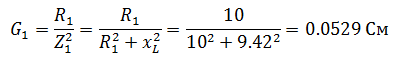 Реактивная проводимость первой ветви равна 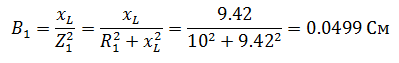 Полная проводимость первой ветви 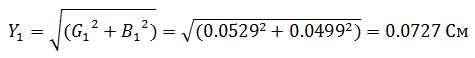 Аналогичный расчет произведем для второй ветви содержащей конденсатор 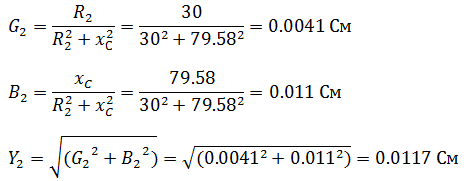 Полная проводимость цепи Токи в цепи определим зная напряжение и проводимости 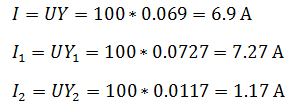 Коэффициент мощности определим по формуле 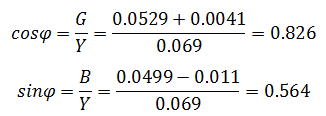 Активная мощность Реактивная мощность Полная мощность
Тема. Решение задач по теме "Переменный ток". Цели: - рассмотреть методы решения задач на использование закона Ома в цепях переменного тока. Ход занятия В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности. При решении задач на законы переменного тока нужно начертить электрическую цепь и проанализировать, как соединены резисторы, источники тока, катушки индуктивности, конденсаторы. Следует помнить, что сила тока, напряжение на различных элементах цепи и электродвижущая сила совершают гармонические колебания с различными фазами. Поэтому при последовательном соединении элементов цепи сила тока на всех участках цепи одинакова в каждый момент времени. Однако напряжение во всей цепи не равно сумме арифметических напряжений на отдельных участках. Оно находится по правилу векторного сложения с помощью векторной диаграммы, при этом учитывается наличие в цепи переменного тока, активного, индуктивного и емкостного сопротивлений. Если активное сопротивление в цепи отсутствует, то для решения задач часто используют формулу Томсона. Для решения задач на превращение электрической энергии в тепловую и механическую используют закон сохранения и превращения энергии. Качественные задачи 1. Вдоль жесткого провода, по которому пропускается переменный ток от городской сети, расположена мягкая тонкая металлическая нить. В одном случае через нить пропускается также переменный ток от городской сети. В другом случае через нить пропускается постоянный ток. Что будет происходить с нитью в каждом случае? 2. Какую траекторию опишет электрон, пролетая между пластинами плоского конденсатора, к которым подведено: 1) постоянное напряжение; 2) переменное напряжение высокой частоты? 3. Как изменится сопротивление, оказываемое линейным проводником току высокой частоты, если этому проводнику придать форму соленоида? 4. Через какую долю периода после замыкания заряженного конденсатора на катушку индуктивности энергия в контуре распределится между конденсатором и катушкой поровну? 5. В каких элементах закрытого колебательного контура (конденсаторе или катушке) сосредоточена энергия в моменты Примеры решения расчетных задач Задача 1. Определите сдвиг фаз колебаний напряжения Решение: Сдвиг фаз между током и напряжением в цепях переменного тока определяется соотношением 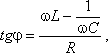 (1) (1)здесь 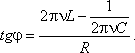 Мощность, которая выделяется в цепи, определится по формуле Для цепи переменного тока справедливо соотношение где Z - полное сопротивление (импеданс) цепи: Следовательно, мощность, которая выделяется в цепи (2) 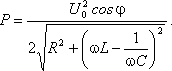 Подставив численные значения в (1), получим Ответ: 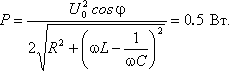 З 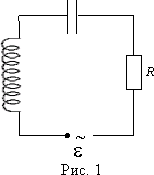 адача 2. Конденсатор неизвестной емкости, катушка с индуктивностью L и сопротивлением R подключены к источнику переменного напряжения адача 2. Конденсатор неизвестной емкости, катушка с индуктивностью L и сопротивлением R подключены к источнику переменного напряжения Решение: Из условия задачи видно, что сила тока и напряжение в цепи меняются синфазно. Это означает, что совпадают индуктивное и емкостное сопротивления. Напряжение на конденсаторе будет равно Поскольку Подставляя (5) в (4), получим: С учетом (3) соотношение (6) примет вид: Поэтому амплитудное значение напряжения между обкладками конденсатора будет равно Ответ: Задача 3. В электрической цепи из двух одинаковых конденсаторов емкости С и катушки с индуктивностью L, соединенных последовательно, в начальный момент времени один конденсатор имеет заряд q0, а второй не заряжен (рис. 2). Как будут изменяться со временем заряды конденсаторов и с 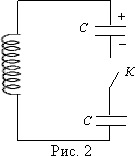 ила тока в контуре после замыкания ключа К? ила тока в контуре после замыкания ключа К?Решение: Цепь, приведенная на рис. 2, представляет собой колебательный контур. Сила тока в нем будет меняться по закону Чтобы ответить на вопрос задачи, нужно найти максимальное значение силы тока I0 и частоту колебаний где Сэкв - емкость системы из двух последовательно соединенных конденсаторов емкостью С: Подставляя значение Сэкв в (8), получим, что частота колебаний в контуре будет равна Подставим значение частоты (9) в выражение для силы тока (7), тогда получим, что сила тока в цепи будет меняться по закону Для определения I0 можно воспользоваться законом сохранения энергии. Пусть в некоторый момент времени заряд одного из конденсаторов равен q1 , тогда заряд второго конденсатора будет q2 = q0 - q1 . В начальный момент времени энергия контура сосредоточена в электрическом поле заряженного конденсатора, в произвольный момент времени она перераспределяется между энергией электрического поля двух заряженных конденсаторов и энергией магнитного поля, сосредоточенного в катушке индуктивности. Следовательно, согласно закону сохранения энергии, Отсюда можно найти зависимость силы тока от заряда q1. Чтобы найти максимальное значение силы тока, нужно взять производную от I по q1 и приравнять ее к нулю. Из последнего выражения видно, что максимальное значение силы тока достигается при Подставляя полученное значение для максимального значения силы тока в (10), получим, что сила тока в цепи будет меняться по закону Чтобы найти закон изменения зарядов на пластинах конденсатора, воспользуемся выражением Решая уравнение, получим: Разные знаки означают, что в начальный момент времени любой конденсатор может либо иметь заряд q0, либо быть незаряженным. Пусть Тогда Ответ: Задача 4. Имеются два колебательных контура с одинаковыми катушками и конденсаторами. В катушку одного из контуров вставили железный сердечник, увеличивший ее индуктивность в n = 4 раза. Найдите отношение резонансных частот контуров и их энергий, если максимальные заряды на конденсаторах одинаковы. Решение: Резонансные частоты контуров могут быть определены по формуле Томсона: Отсюда Ответ: 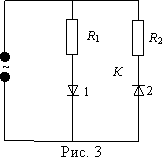 Задача 5. Два сопротивления R1 и R2 и два диода подключены к источнику переменного тока с напряжением U так, как показано на рис. 3. Найдите среднюю мощность, выделяющуюся в цепи. Решение: Ток половину периода идет через один диод (например, 1). За это время на сопротивлении R1 выделяется средняя мощность В течение второго полупериода ток идет через диод 2, выделяя на нем среднюю мощность Таким образом, за полный период выделяется средняя мощность Ответ: Задачи для самостоятельной работы 1 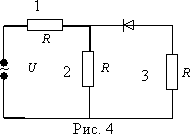 . Три одинаковых резистора 1, 2, 3, имеющих сопротивление R, включены в цепь с диодом, как показано на рис. 4. Определите мощность, выделяющуюся на резисторе 3. Напряжение источника переменного тока равно U. . Три одинаковых резистора 1, 2, 3, имеющих сопротивление R, включены в цепь с диодом, как показано на рис. 4. Определите мощность, выделяющуюся на резисторе 3. Напряжение источника переменного тока равно U.Ответ: 2. На какую длину волны настроен колебательный контур, если он состоит из катушки с индуктивностью L = 2 Ответ: 3. Электропечь сопротивлением R = 22 Ом питается от генератора переменного тока. Определите количество теплоты Q, выделяемое печью за время t = 1 час, если амплитуда силы тока I0 = 10 А. Ответ: 4. Заряженный конденсатор емкостью С = 0,2 мкФ подключили к катушке с индуктивностью L = 8 мГн. Через какое время от момента подключения энергия электрического поля конденсатора станет равной энергии магнитного поля катушки? Ответ: 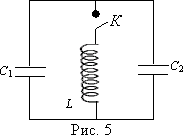 5. В колебательном контуре индуктивность катушки L = 2,5 мГн, а емкости конденсаторов C1 = 2,0 мкФ, C2 = 3,0 мкФ. Конденсаторы зарядили до напряжения U = 180 В и замкнули ключК (рис. 5). Определите период Т собственных колебаний и амплитудное значение силы тока I0 через катушку. Активное сопротивление контура пренебрежимо мало. Ответ: 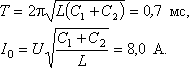 6  . Колебательный контур через ключ К подключен к источнику электродвижущей силы с некоторым внутренним сопротивлением r (рис. 6). Первоначально ключ К замкнут. После установления стационарного режима ключ размыкают и в контуре возникают колебания с периодом Т. При этом амплитуда напряжения на конденсаторе в n раз больше электродвижущей силы батареи. Определите индуктивность L катушки и емкость С конденсатора. Активное сопротивление контура пренебрежимо мало. . Колебательный контур через ключ К подключен к источнику электродвижущей силы с некоторым внутренним сопротивлением r (рис. 6). Первоначально ключ К замкнут. После установления стационарного режима ключ размыкают и в контуре возникают колебания с периодом Т. При этом амплитуда напряжения на конденсаторе в n раз больше электродвижущей силы батареи. Определите индуктивность L катушки и емкость С конденсатора. Активное сопротивление контура пренебрежимо мало.Ответ:  7. Заряженный конденсатор емкости С замыканием ключа К подключают к двум параллельно соединенным катушкам с индуктивностями L1 и L2(рис.7). Максимальный ток, протекающий через катушку L1, равен I1. Определите первоначальный заряд q0 на конденсаторе. Сопротивление катушек и подводящих проводов пренебрежимо мало. Ответ: Рекомендуемая литература 1. Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Электродинамика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 11-82. 2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 188-202. 3. Готовцев В.В. Лучшие задачи по электричеству. - М.; Ростов н/Д: Издательский центр "Март", 2004. - С. 172-188. |