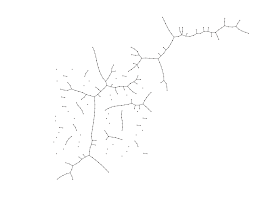
проект. Решение задачи поиска минимальных остовных деревьев ( mst minimum spanning tree) является распространенной задачей в различных областях исследований распознавание различных объектов,
 Скачать 1.81 Mb. Скачать 1.81 Mb.
|
Введение Решение задачи поиска минимальных остовных деревьев ( MST — minimum spanning tree) является распространенной задачей в различных областях исследований: распознавание различных объектов, компьютерное зрение, анализ и построение сетей (например, телефонных, электрических, компьютерных, дорожных и т.д.), химия и биология и многие другие. Существует по крайней мере три известных алгоритма, решающих данную задачу: Борувки, Крускала и Прима. Обработка больших графов (занимающих несколько ГБ) является достаточно трудоемкой задачей для центрального процессора (CPU) и является востребованной в данное время. Все более широкое распространение получают графические ускорители (GPU), способные показывать намного большую производительность, чем CPU. Но задача MST, как и многие задачи по обработке графов, плохо ложатся на архитектуру GPU. В данной статье будет рассмотрена реализация данного алгоритма на GPU. Также будет показано, как можно использовать CPU для построения гибридной реализации данного алгоритма на общей памяти одного узла (состоящего из GPU и нескольких CPU). Вариант 3- Алгоритм MST (Algorithm based on Minimum Spanning Tree) 1.Описание алгоритма кластерного анализа (со ссылками на литературу) Назначение: кластеризация больших наборов произвольных данных. Достоинства: выделяет кластеры произвольной формы, в т.ч. кластеры выпуклой и впуклой формы, выбирает из нескольких оптимальных решений самое оптимальное. Описание алгоритма [13] Шаг 1 Построение минимального остовного дерева: Связный, неориентированный граф с весами на ребрах G(V, E), в котором V – множество вершин(контактов), а E – множество их возможных попарных соединений (ребер), для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость соединения). Алгоритм Борувки: 1. Для каждой вершины графа находимо ребро с минимальным весом. 2. Добавляем найденные ребра к остовному дереву, при условии их безопасности. 3. Находим и добавляем безопасные ребра для несвязанных вершин к остовному дереву. 4. Общее время работы алгоритма: O(ELogV). Алгоритм Крускала: 1. Обход ребер по возрастанию весов. При условии безопасности ребра добавляем его к основному дереву. 2. Общее время работы алгоритма: O(ELogE). Алгоритм Прима: 1. Выбор корневой вершины. 2. Начиная с корня добавляем безопасные ребра к остовному дереву. Общее время работы алгоритма: O(ELogV). Шаг 2 Разделение на кластеры. Дуги с наибольшими весами разделяют кластеры. Принцип работы описанных выше групп методов в виде дендрограммы показан на рис. 1 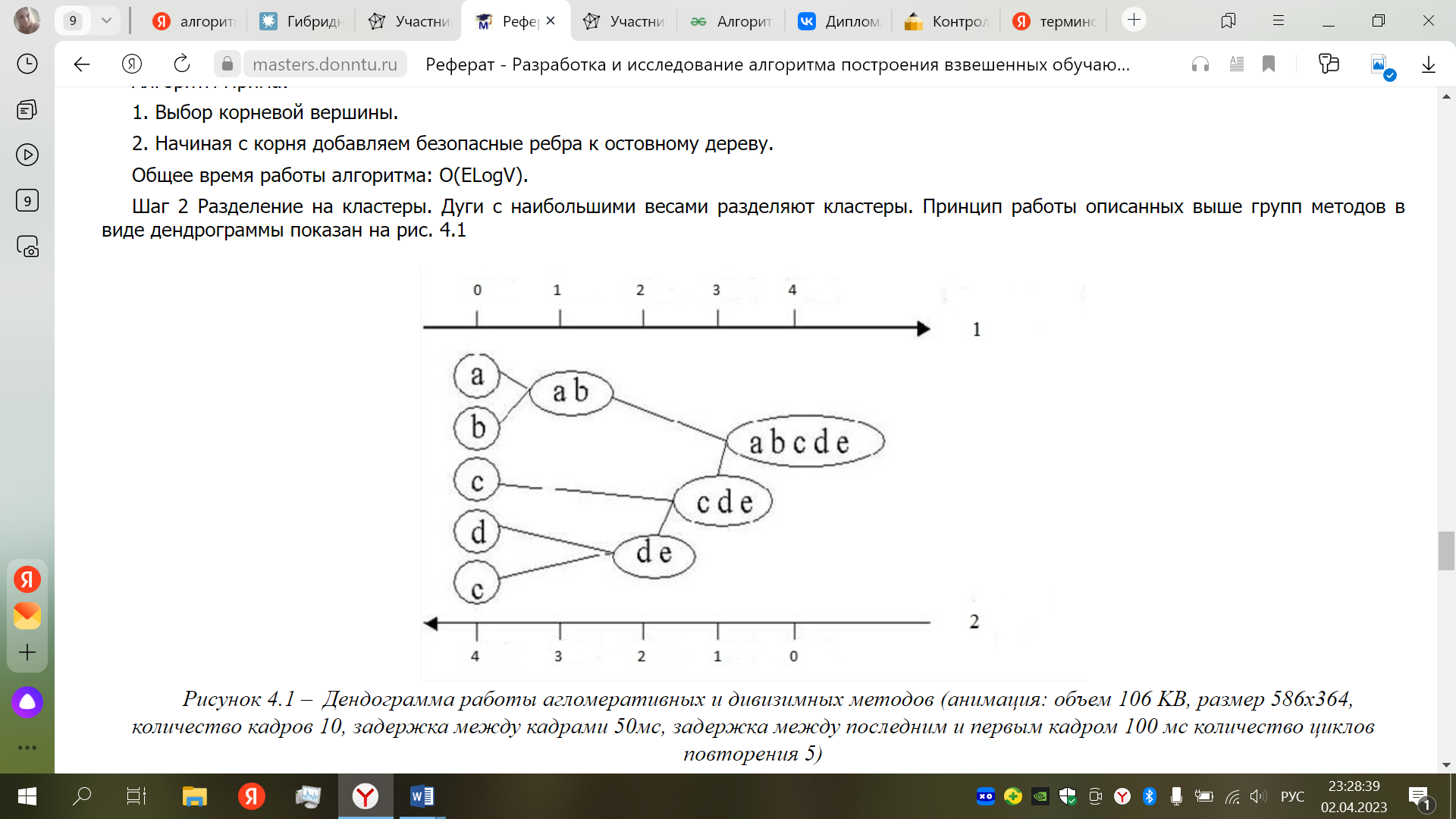 .1 – Дендограмма работы агломеративных и дивизимных методов (анимация: объем 106 KB, размер 586x364, количество кадров 10, задержка между кадрами 50мс, задержка между последним и первым кадром 100 мс количество циклов повторения 5) Алгоритм k-средних (k-means) Наиболее распространен среди неиерархических методов алгоритм k-средних, также называемый быстрым кластерным анализом. Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров. Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних, – наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа k может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции. Общая идея алгоритма: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга. Описание алгоритма: 1. Первоначальное распределение объектов по кластерам. Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр. Выбор начальных центроидов может осуществляться следующим образом: – выбор k-наблюдений для максимизации начального расстояния; – случайный выбор k-наблюдений; – выбор первых k-наблюдений. В результате каждый объект назначен определенному кластеру. 2.Итеративный процесс. Вычисляются центры кластеров, которыми затем и далее считаются покоординатные средние кластеров. Объекты опять перераспределяются. Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий: – кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации; – число итераций равно максимальному числу итераций. На рис. 2 приведен пример работы алгоритма k-средних для k, равного двум. 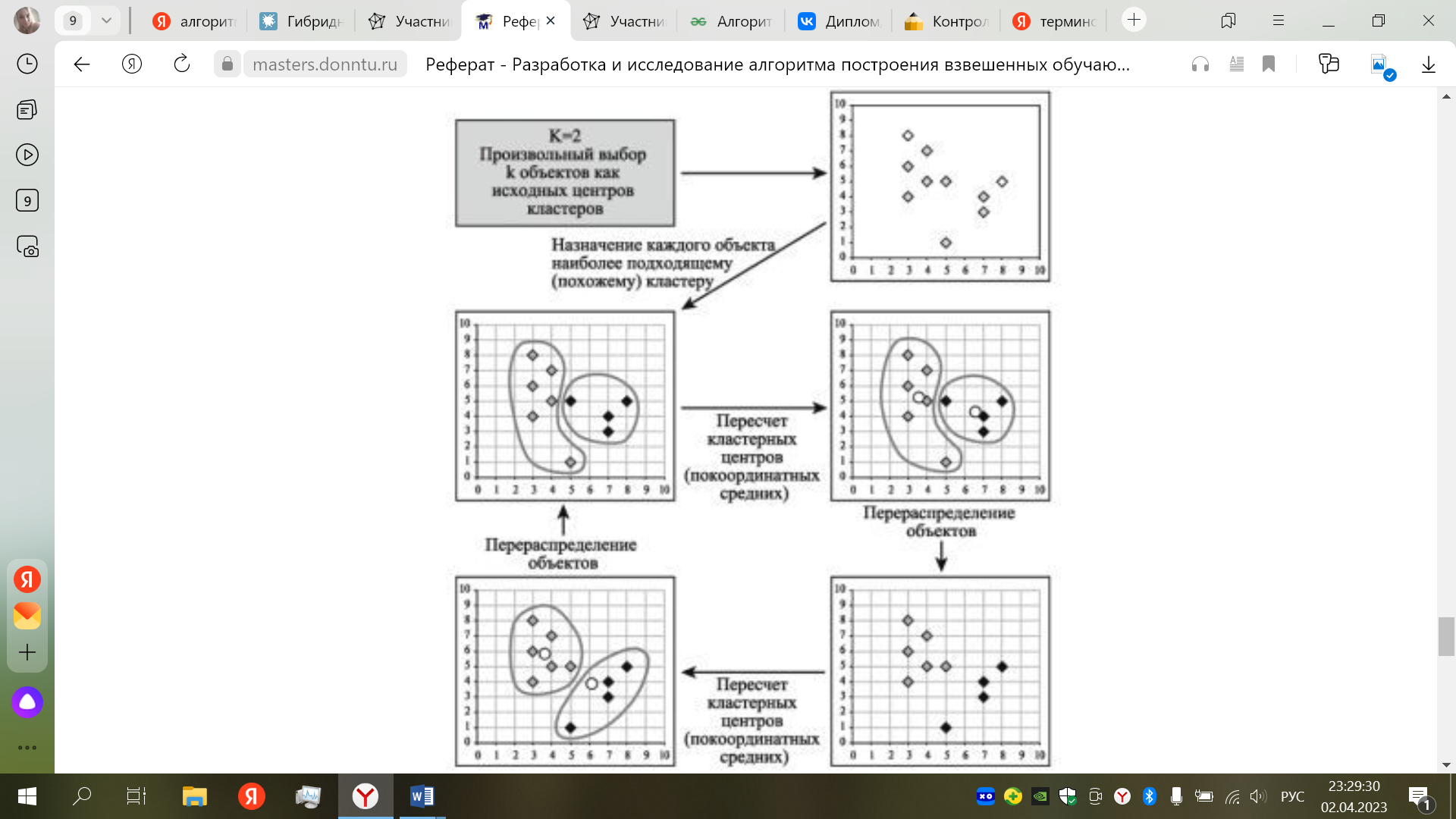 .2 – Пример работы алгоритма k-средних (k=2) Выбор числа кластеров является сложным вопросом. Если нет предположений относительно этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5 и т.д., сравнивая полученные результаты. После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера. При хорошей кластеризации должны быть получены сильно отличающиеся средние для всех измерений или хотя бы большей их части. Достоинства алгоритма k-средних: – простота использования; – быстрота использования; – понятность и прозрачность алгоритма. Недостатки алгоритма k-средних: – алгоритм слишком чувствителен к выбросам, которые могут искажать среднее. Возможным решением этой проблемы является использование модификации алгоритма – алгоритм k-медианы; – алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных. 2.Листинг программы кластерного анализа. Обширный класс алгоритмов кластеризации основан на представлении выборки в виде графа. Вершинам графа соответствуют объекты выборки, а рёбрам — попарные расстояния между объектами. Достоинством графовых алгоритмов кластеризации является наглядность, относительная простота реализации и возможность вносить различные усовершенствования, опираясь на простые геометрические соображения. Алгоритм минимального покрывающего дерева (MST) строит граф из N-1 рёбер так, чтобы они соединяли все N точек и обладали минимальной суммарной длиной. Такой граф называется кратчайшим незамкнутым путём, минимальным покрывающим деревом или каркасом графа. Описание работы алгоритма: Найти пару точек с наименьшим расстоянием (весом ребра) и соединить их ребром; пока в выборке остаются изолированные точки: найти изолированную точку, ближайшую к некоторой неизолированной; соединить эти две точки ребром; удалить K-1 самых длинных рѐбер; На последнем шаге алгоритм удаляет из полученного графа K-1 самых длинных рёбер, что приводит к распаду графа на отдельные связанные компоненты, которые и будут искомыми кластерами. Общеизвестны два недостатка этого алгоритма: ограниченная применимость. Алгоритм наиболее подходит для выделения кластеров типа сгущений или лент. Наличие разреженного фона или «узких перемычек» между кластерами приводит к неадекватным результатам; высокая трудоёмкость — для построения кратчайшего незамкнутого пути требуется O(N^3) операций. Для работы с графами будет использоваться NetworkX — библиотека для создания и манипуляции графами. Кроме этого, она предоставляет готовую реализацию алгоритма нахождения минимального остовного дерева и удобное API для визуализации результатов. Для начала необходимо получить исходные данные и расстояния между всеми элементами набора. from scipy.spatial.distance import pdist names, data = get_data() dist = pdist(data, 'euclidean') Функции get_data() и pdist() были описаны в первой заметке, поэтому не будем на них останавливаться. Следом попробуем построить граф, представляющий наш исходный набор данных. Каждая вершина этого графа будет обозначать отдельный объект исходной выборки и будет связана со всеми остальными вершинами посредством взвешенных рёбер. Вес каждого ребра будет равен расстоянию близости между объектами. from collections import deque import networkx as nx s = nx.Graph() s.add_nodes_from(names) dq = deque(dist) len_x = len(names) for x in xrange(len_x - 1): for y in xrange(x + 1, len_x): s.add_edge(names[x], names[y], weight=dq.popleft()) В переменной s содержится исходный граф нашего набора данных. Следующим шагом построим минимальное покрывающее дерево полученного графа и отобразим гистограмму весов рёбер в нём (дабы выбрать пороговый уровень веса). import matplotlib.pyplot as plt mst = nx.minimum_spanning_tree(s) plt.hist([edge[2]['weight'] for edge in mst.edges_iter(data=True)], 100, color='red', alpha=0.3) 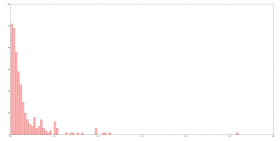 Теперь создадим ещё один граф, включающий все вершины нашего исходного набора, но добавим в него только те рёбра, которые являлись частью остовного дерева и весили меньше порогового уровня в 0.05 (выбран чисто эмпирически по гистограмме). r = nx.Graph() r.add_nodes_from(names) edges = [edge for edge in mst.edges_iter(data=True) if edge[2]['weight'] <= 0.05] r.add_edges_from(edges) Как вы могли заметить, в отличии от классического алгоритма MST, я предпочёл отрезать рёбра не по количеству кластеров, а по пороговому уровню, как в иерархическом алгоритме. Это позволило снизить влияние на результат кластеризации качество предварительной подготовки данных. Что же, осталось лишь отобразить результат. Для этого в NetworkX также есть встроенные средства, а именно функция draw_graphviz. Интерес для нас представляет само остовное дерево и полученный граф кластеров. def graph_draw(g): """Draw graph""" plt.figure() nx.draw_graphviz(g, with_labels=False, node_size=3, prog='neato') graph_draw(mst) graph_draw(r) plt.show()
3. Результаты работы программы (скриншоты). Описание формата представления графов Кратко рассмотрим структуру хранения неориентированного взвешенного графа, так как в дальнейшем она будет упоминаться и преобразовываться. Граф задается в сжатом CSR (Compressed Sparse Row) [1] формате. Данный формат широко распространен для хранения разреженных матриц и графов. Для графа с N вершинами и M ребрами необходимо три массива: X, A и W. Массив X размера N + 1, остальные два – 2*M, так как в неориентированном графе для любой пары вершин необходимо хранить прямую и обратную дуги. В массиве X хранится начало и конец списка соседей, которые хранятся в массиве А, то есть весь список соседей вершины J находится в массиве A с индекса X[J] до X[J+1], не включая его. По аналогичным индексам хранятся веса каждого ребра из вершины J. Для иллюстрации на рисунке ниже слева показан граф из 6 вершин, записанный с помощью матрицы смежности, а справа – в CSR формате (для упрощения, вес каждого ребра не указан). 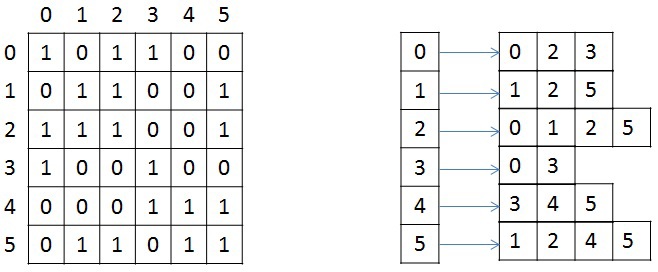 Тестируемые графы Сразу опишу на каких графах происходило тестирование, так как для описания алгоритмов преобразования и алгоритма MST потребуется знание структуры рассматриваемых графов. Для оценки производительности реализации используются два вида синтетических графов: RMAT-графы и SSCA2-графы. R-MAT-графы хорошо моделируют реальные графы из социальных сетей, Интернета [2]. В данном случае рассматриваются RMAT-графы со средней степенью связности вершины 32, а количество вершин является степенью двойки. В таком RMAT-графе имеется одна большая связная компонента и некоторое количество небольших связных компонент или висящих вершин. SSCA2-граф представляет собой большой набор независимых компонент, соединенных ребрами друг с другом [3]. SSCA2-граф генерируется таким образом, чтобы средняя степень связности вершины была близка к 32, а eё количество вершин также является степенью двойки. Таким образом, рассматриваются два совершенно разных по структуре графа. Преобразование входных данных Так как тестирование алгоритма будет производиться на графах RMAT и SSCA2, которые получаются с помощью генератора, то для улучшения производительности алгоритма необходимо проделать некоторые преобразования. Все преобразования не будут учтены в подсчете производительности. Локальная сортировка списка вершин Для каждой вершины выполним сортировку ее списка соседей по весу, в порядке возрастания. Это позволит частично упростить выбор минимального ребра на каждой итерации алгоритма. Так как данная сортировка является локальной, то она не дает полное решение задачи. Перенумерация всех вершин графа Занумеруем вершины графа таким образом, чтобы наиболее связные вершины имели наиболее близкие номера. В результате данной операции в каждой связной компоненте разница между максимальным и минимальным номером вершины будет наименьшей, что позволит лучшим образом использовать маленький кэш графического процесса. Стоит отметить, что для RMAT графов данная перенумерация не дает существенного эффекта, так как в данном графе присутствует очень большая компонента, которая не помещается в кэш даже после применения данной оптимизации. Для SSCA2 графов эффект от данного преобразования заметен больше, так как в данном графе большое количество небольших компонент. Отображение весов графа в целые числа В данной задаче нам не надо производить каких-либо операций над весами графа. Нам необходимо уметь сравнивать веса двух ребер. Для этих целей можно использовать целые числа, вместо чисел двойной точности, так как скорость обработки чисел одинарной точности на GPU намного выше, чем двойной. Данное преобразование можно выполнить для графов, у которых количество уникальных ребер не превосходит 2^32 (максимальное количество различных чисел, помещающихся в unsigned int). Если средняя степень связности каждой вершины равна 32м, то самый большой граф, который можно обработать с применением данного преобразования, будет иметь 2^28 вершин и будет занимать в памяти 64 ГБ. На сегодняшний день наибольшее количество памяти в ускорителях NVidia Tesla k40[4] / NVidia Titan X[5] и AMD FirePro w9100[6] составляет 12ГБ и 16ГБ соответственно. Поэтому на одном GPU с применением данного преобразования можно обработать достаточно большие графы. Сжатие информации о вершинах Данное преобразование применимо только к графам SSCA2 из-за их структуры. В данной задаче решающую роль играет производительность памяти всех уровней: начиная от глобальной памяти и заканчивая кэшем первого уровня. Для снижения трафика между глобальной памятью и L2 кэшем, можно хранить информацию о вершинах в сжатом виде. Изначально информация о вершинах представлена в виде двух массивов: массива X, в котором хранятся начало и конец списка соседей в массиве А (пример только для одной вершины): 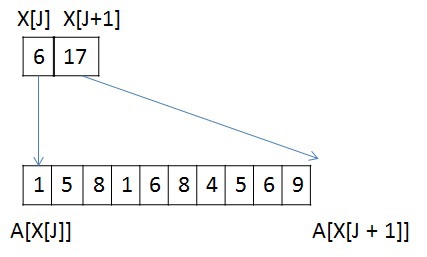 У вершины J есть 10 вершин-соседей, и если номер каждого соседа хранится с использованием типа unsigned int, то для хранения списка соседей вершины J потребуется 10 * sizeof(unsigned int) байт, а для всего графа — 2 * M * sizeof(unsigned int) байт. Будем считать, что sizeof(unsigned int) = 4 байта, sizeof(unsigned short) = 2 байта, sizeof(unsigned char) = 1 байт. Тогда для данной вершины необходимо 40 байт для хранения списка соседей. Не трудно заметить, что разница между максимальным и минимальным номером вершины в этом списке равна 8, причем для хранения данного числа необходимо всего 4 бита. Исходя из тех соображений, что разница между максимальным и минимальным номером вершины может быть меньше, чем unsigned int, можно представить номер каждой вершины следующим образом: base_J + 256 * k + short_endV, где base_J — например, минимальный номер вершины из всего списка соседей. В данном примере это будет 1. Данная переменная будет иметь тип unsigned int и таких переменных будет столько, сколько вершин в графе; Далее посчитаем разницу между номером вершины и выбранной базой. Так как в качестве базы мы выбрали наименьшую вершину, то данная разница будет всегда положительной. Для графа SSCA2 данная разница будет помещаться в unsigned short. short_endV — это остаток от деления на 256. Для хранения данной переменной будем использовать тип unsigned char; а k — есть целая часть от деления на 256. Для k выделим 2 бита (то есть k лежит в пределах от 0 до 3). Выбранное представление является достаточным для рассматриваемого графа. В битовом представление это выглядит так: 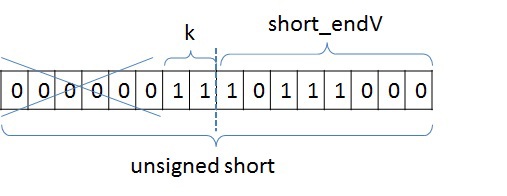 Тем самым для хранения списка вершин требуется (1 + 0,25) * 10 + 4 = 16,5 байт для данного примера, вместо 40 байт, а для всего графа: (2 * M + 4 * N + 2 * M / 4) вместо 2 * M * 4. Если N = 2 * M / 32, то общий объем уменьшится в (8 * M) / (2 * M + 8 * M / 32 + 2 * M / 4) = 2.9 раз Общее описание алгоритма Для реализации алгоритма MST был выбран алгоритма Борувки. Базовое описание алгоритма Борувки и иллюстрация его итераций хорошо представлена по этой ссылке [7]. Согласно алгоритму, все вершины изначально включены в минимальное дерево. Далее необходимо выполнить следующие шаги: Найти минимальные ребра между всеми деревьями для их последующего объединения. Если на данном шаге не выбрано ни одно ребро, то ответ задачи получен Выполнить объединение соответствующих деревьев. Данный шаг разбивается на два этапа: удаление циклов, так как два дерева могут в качестве кандидата на объединение указать друг друга, и этап объединения, когда выбирается номер дерева, в которое входят объединяемые поддеревья. Для определенности будем выбирать минимальный номер. Если в ходе объединения осталось лишь одно дерево, то ответ задачи получен. Выполнить перенумерацию полученных деревьев для перехода на первый шаг (чтобы все деревья имели номера от 0 до k) Этапы алгоритма В общем реализованный алгоритм выглядит следующим образом: 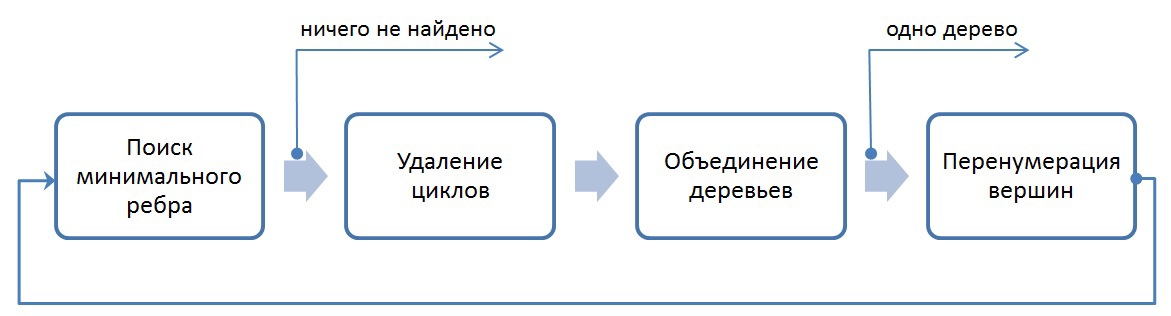 Выход из всего алгоритма происходит в двух случаях: если все вершины после N итераций объединены в одно дерево, либо если невозможно найти минимальное ребро из каждого дерева (в таком случае минимальные остовные деревья найдены). 1. Поиск минимального ребра. Сначала каждая вершина графа помещается в отдельное дерево. Далее происходит итеративный процесс объединения деревьев, состоящий из четырех рассмотренных выше процедур. Процедура поиска минимального ребра позволяет выбрать именно те ребра, которые будут входить в минимальное остовное дерево. Как было описано выше, на входе у данной процедуры преобразованный граф, хранящийся в формате CSR. Так как для списка соседей была выполнена частичная сортировка ребер по весу, то выбор минимальной вершины сводится к просмотру списка соседей и выбора первой вершины, которая принадлежит другому дереву. Если предположить, что в графе нет петель, то на первом шаге алгоритма выбор минимальной вершины сводится к выбору первой вершины из списка соседей для каждой рассматриваемой вершины, потому что список соседних вершин (которые составляют вместе с рассматриваемой вершиной ребра графа), отсортированы по возрастанию веса ребра и каждая вершина входит в отдельное дерево. На любом другом шаге необходимо просмотреть список всех соседних вершин по порядку и выбрать ту вершину, которая принадлежит другому дереву. Почему же нельзя выбрать вторую вершину из списка соседних вершин и положить данное ребро минимальным? После процедуры объединения деревьев (которая будет рассмотрена далее) может возникнуть ситуация, что некоторые вершины из списка соседних могут оказаться в том же дереве, что и рассматриваемая, тем самым данное ребро будет являться петлей для данного дерева, а по условию алгоритма необходимо выбирать минимальное ребро до других деревьев. Для реализации обработки вершин и выполнения процедуры поиска, объединения и слияния списков хорошо подходит Union Find [8]. К сожалению, не все структуры оптимально обрабатываются на GPU. Наиболее выгодно в данной задаче (как и в большинстве других) использовать непрерывные массивы в памяти GPU, вместо связных списков. Ниже будут рассмотрены похожие алгоритмы для поиска минимального ребра, объединения сегментов, удаления циклов в графе. Рассмотрим алгоритм поиска минимального ребра. Его можно представить в виде двух шагов: выбор минимального ребра исходящего из каждой вершины (которая входит в какой-то сегмент) рассматриваемого графа; выбор ребра минимального веса для каждого дерева. Для того, чтобы не перемещать информацию о вершинах, записанную в формате CSR, будем использовать два вспомогательных массива, которые будут хранить индекс начала и конца массива А списка соседей. Два данных массива будут обозначать сегменты списков вершин, принадлежащих одному дереву. Например, на первом шаге массив начал или нижних значений будет иметь значения 0..N массива X, а массив концов или верхних значений будет иметь значения 1..N+1 массива X. А далее, после процедуры объединения деревьев (которая будет рассмотрена далее), данные сегменты перемешаются, но массив соседей А не будет изменен в памяти. Оба шага могут быть выполнены параллельно. Для выполнения первого шага необходимо просмотреть список соседей каждой вершины (или каждого сегмента) и выбрать первое ребро, принадлежащее другому дереву. Можно выделить один warp (состоящий из 32х нитей) для просмотра списка соседей каждой вершины. Стоит помнить, что несколько сегментов массива соседних вершин А могут лежать не подряд и принадлежать одному дереву (красным выделены сегменты, принадлежащие дереву 0, а зеленым — дереву 1): 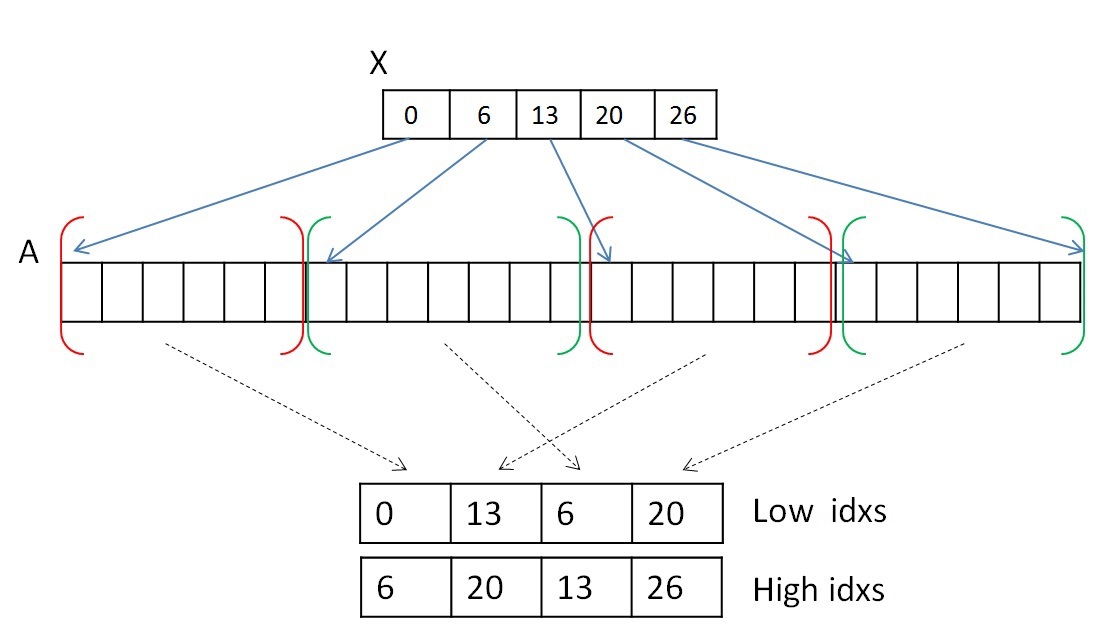 В силу того, что каждый сегмент списка соседей отсортирован, то не обязательно просматривать все вершины. Так как один warp состоит из 32х нитей, то просмотр будет осуществляться порциями по 32 вершины. После того, как просмотрены 32 вершины, необходимо объединить результат и если ничего не найдено, то просмотреть следующие 32 вершины. Для объединения результата можно воспользоваться алгоритмом scan [9]. Реализовать данный алгоритм внутри одного warp'а можно с помощью разделяемой памяти или с помощью новых shfl-инструкций [10] (доступных с архитектуры Kepler), которые позволяют обменяться данными между нитями одного warp'а за одну инструкцию. В результате проведения экспериментов выяснилось, что shfl-инструкции позволяют ускорить примерно в два раза работу всего алгоритма. Таким образом, данная операция может быть выполнена с использованием shfl-инструкций, например, так: unsigned idx = blockIdx.x * blockDim.x + threadIdx.x; // глобальный индекс нити unsigned lidx = idx % 32; #pragma unroll for (int offset = 1; offset <= 16; offset *= 2) { tmpv = __shfl_up(val, (unsigned)offset); if(lidx >= offset) val += tmpv; } tmpv = __shfl(val, 31); // рассылка всем нитям последнего значения. Если получено значение 1, то какая-то нить нашла // минимальное ребро, иначе необходимо продолжить поиск. В результате данного шага для каждого сегмента будет записана следующая информация: номер вершины в массиве А, входящее в ребро минимального веса и вес самого ребра. Если ничего не найдено, то в номер вершины можно записать, например, число N + 2. Второй шаг необходим для редуцирования выбранной информации, а именно — выбор ребра с минимальным весом для каждого из деревьев. Данный шаг делается из-за того, что сегменты, принадлежащие одному и тому же дереву, просматриваются параллельно и независимо, и для каждого из сегментов выбирается ребро минимального веса. В данном шаге один warp может редуцировать информацию по каждому дереву (по нескольким сегментам) и для редукции можно также применить shfl-инструкции. После выполнения данного шага будет известно с каким деревом каждое из деревьев соединено минимальным ребром (если оно существует). Для записи данной информации введем еще два вспомогательных массива, в одном из которых будем хранить номера деревьев, до которых есть минимальное ребро, во втором — номер вершины в исходном графе, которая является корнем входящих в дерево вершин. Результат данного шага проиллюстрирован ниже: 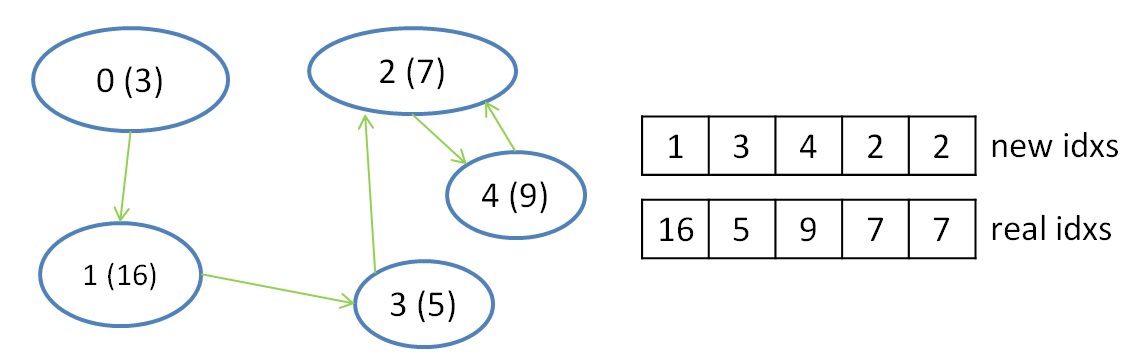 Стоит отметить, что для работы с индексами необходимо еще два массива, которые помогают конвертировать первоначальные индексы в новые индексы и получать по новому индексу первоначальный. Эти так называемые таблицы переконвертации индексов обновляются с каждой итерацией алгоритма. Таблица получения нового индекса по первоначальному индексу имеет размер N — количества вершин в графе, а таблица получения первоначального индекса по новому сокращается с каждой итерацией и имеет размер, равный количеству деревьев на какой-либо выбранной итерации алгоритма (на первой итерации алгоритма эта таблица имеет также размер N). 2. Удаление циклов. Данная процедура необходима для удаления циклов между двумя деревьями. Данная ситуация возникает тогда, когда у дерева N1 минимальное ребро до дерева N2, а у дерева N2 минимальное ребро до дерева N1. На картинке выше, есть цикл только между двумя деревьями с номерами 2 и 4. Так как деревьев на каждой итерации становится меньше, то будем выбирать минимальный номер из двух деревьев, составляющих цикл. В данном случае, 2 будет указывать на 2, а 4 продолжит указывать на 2. С помощью таких проверок можно определить такой цикл и устранить его в пользу минимального номера: unsigned i = blockIdx.x * blockDim.x + threadIdx.x; unsigned local_f = сF[i]; if (сF[local_f] == i) { if (i < local_f) { F[i] = i; . . . . . . . } } Данная процедура может быть выполнена параллельно, так как каждая вершина может быть обработана независимо и записи в новый массив вершин без циклов не пересекаются. 3. Объединение деревьев. Данная процедура производит объединение деревьев в более крупные. Процедура удаления циклов между двумя деревьями является по сути предобработкой перед данной процедурой. Она позволяет избежать зацикливания при объединении деревьев. Объединение деревьев представляет собой процесс выбора нового корня путем изменения ссылок. Если допустим дерево 0 указывало на дерево 1, а в свою очередь дерево 1 указывало на дерево 3, то можно сменить ссылку дерева 0 с дерева 1 на дерево 3. Данное изменение ссылки стоит производить, если изменение ссылки не приводит к появлению цикла между двумя деревьями. Рассматривая пример выше, после процедур удаления циклов и объединения деревьев останется только одно дерево с номером 2. Процесс объединения можно представить примерно так: 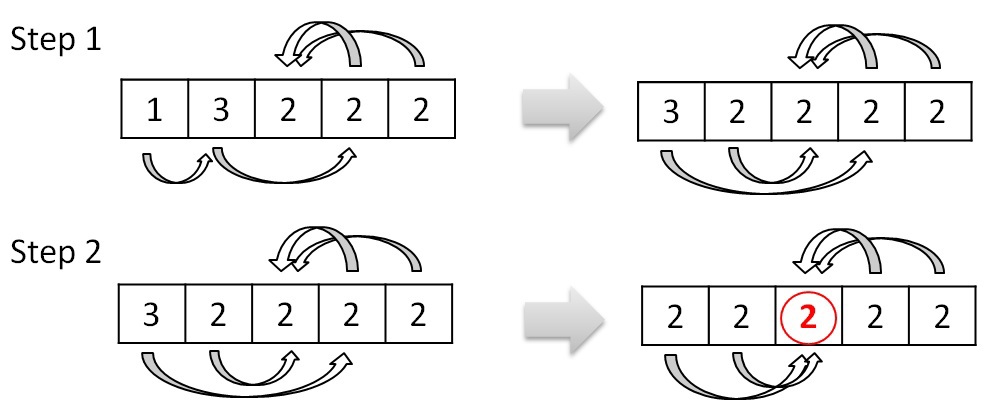 Структура графа и принцип его обработки таков, что не возникнет ситуации, когда будет происходить зацикливание процедуры и она также может быть выполнена параллельно. 4. Перенумерация вершин (деревьев). После выполнения процедуры объединения необходимо перенумеровать полученные деревья так, чтобы их номера шли подряд от 0 до P. По построению, новые номера должны получить элементы массива, удовлетворяющие условию F[i] == i (для рассмотренного примера выше, данному условию удовлетворяет только элемент с индексом 2). Тем самым, с помощью атомарных операций можно разметить весь массив новыми значениями от 1… (P+1). Далее выполнить заполнение таблиц получения нового индекса по первоначальному и первоначального индекса по новому:  Работа с данными таблицами описана в процедуре поиска минимального ребра. Следующая итерация не может корректно выполняться без обновления данных таблиц. Все описанные операции выполняются параллельно и на GPU. Подведем небольшой итог. Все 4 процедуры выполняются параллельно и на графическом ускорителе. Работа ведется с одномерными массивами. Единственная трудность — во всех данных процедурах присутствует косвенная индексация. И чтобы уменьшить кэш-промахи от такой работы с массивами, были использованы различные перестановки графа, описанные в самом начале. Но, к сожалению, не для каждого графа удается сократить потери от косвенной индексации. Как будет показано далее, при таком подходе на RMAT-графах достигается не очень высокая производительность. Поиск минимального ребра занимает до 80% времени работы всего алгоритма, тогда как на остальные приходится оставшиеся 20%. Это связано с тем, что в процедурах объединения, удаления циклов и перенумерации вершин работа ведется с массивами, длина которых постоянно уменьшается (от итерации к итерации). Для рассматриваемых графов необходимо проделать порядка 7-8 итераций. Это означает, что количество обрабатываемых вершин уже на первом шаге становится намного меньше, чем N / 2. В то время как в основной процедуре поиска минимального ребра работа идет с массивами вершин А и массивом весов W (хоть и выбираются определенные элементы). Дополнительно к хранению графа было использовано еще несколько массивов длины N: массив нижних значений и массив верхних значений. Использовались для работы с сегментами массива А; массив-таблица для получения первоначального индекса по новому; массив-таблица для получения нового индекса по первоначальному; массив для номеров вершин и массив для соответствующих им весов, использующиеся во втором шаге процедуры поиска минимального ребра; вспомогательный массив, позволяющий определить в первом шаге процедуры поиска минимального ребра к какому дереву принадлежит тот или иной сегмент. Гибридная реализация процедуры поиска минимального ребра. Алгоритм описанный выше в конечном счете не плохо выполняется на одном GPU. Решение данной задачи организовано таким образом, что можно попробовать распараллелить данную процедуру еще и на CPU. Конечно, это можно сделать только на общей памяти, и для этого был использовал стандарт OpenMP и передача данных между CPU и GPU по шине PCIe. Если представить выполнение процедур на одной итерации на линии времени, то картина при использовании одного GPU будет примерно такой:  Изначально все данные о графе хранятся как на CPU так и на GPU. Для того, чтобы CPU мог считать, необходимо передать информацию о перемещенных во время объединения деревьев сегментах. Также для того, чтобы GPU продолжил итерацию алгоритма, необходимо вернуть посчитанные данные. Логичным было бы использование асинхронного копирования между хостом и ускорителем:  Алгоритм на CPU повторяет алгоритм, используемый на GPU, только для распараллеливания цикла используется OpenMP [11]. Как и стоило ожидать, CPU считает не так быстро как GPU, да и накладные расходы на копирование тоже мешают. Чтобы CPU успевало посчитать свою часть, данные для обсчета надо делить в отношении 1: 5, то есть не более 20%-25% отдавать на CPU, а остальное обсчитывать на GPU. Остальные процедуры не выгодно считать и там и там, так как они занимают очень мало времени, а накладные расходы и медленная скорость CPU только увеличивают время алгоритма. Также очень важна скорость копирования между CPU и GPU. На тестируемой платформе поддерживался PCIe 3.0, который позволял достигать 12GB/s. На сегодняшний день количество оперативной памяти на GPU и CPU существенно отличается в пользу последнего. На тестовой платформе было установлено 6 GB GDDR5, в то время как на CPU было целых 48 GB. Ограничения по памяти на GPU не позволяют обсчитывать большие графы. И тут нам может помочь CPU и технология Unified Memory [12], которая позволяет обращаться с GPU в память CPU. Так как информация о графе необходима только в процедуре поиска минимального ребра, то для больших графов можно сделать следующее: сначала поместить все вспомогательные массивы в памяти GPU, а далее расположить часть массивов графа (массив соседей A, массив X и массив весов W) в памяти GPU, а то что не уместилось — в памяти CPU. Далее, во время счета, можно делить данные так, чтобы на CPU обрабатывалась та часть, которая не поместилась на GPU, а GPU минимально использовал доступ в память CPU (так как доступ в память CPU с графического ускорителя осуществляется через шину PCIe на скорости не более 15 GB/s). Заранее известно в какой пропорции были поделены данные, поэтому для того, чтобы определить в какую память надо обращаться — в GPU или CPU — достаточно ввести константу, показывающую в какой точке разделены массивы и с помощью одной проверки в алгоритме на GPU можно определить куда надо делать обращение. Расположение в памяти данных массивов можно представить примерно так:  Тем самым можно обработать графы, которые изначально не помещаются на GPU даже при использовании описанных алгоритмов сжатия, но с меньшей скоростью, так как пропускная способность PCIe очень ограничена. Результаты тестирования Тестирование производилось на GPU NVidia GTX Titan, у которого 14 SMX с 192 cuda ядрами (всего 2688) и на процессоре 6 cores (12th) Intel Xeon E5 v1660 с частотой 3,7 Ггц. Графы, на которых производилось тестирование, описаны выше. Приведу только некоторые характеристики:
Видно, что граф масштаба 16 достаточно мал (порядка 25 МБ) и даже без преобразований легко помещается в кэш одного современного процессора Intel Xeon. А так как веса графа занимают 2/3 от общего количества, то фактически необходимо обрабатывать порядка 8 МБ, что всего примерно в 5 раза больше L2 кэша GPU. Однако большие графы требуют достаточного количества памяти и даже граф 24 масштаба уже не помещается в память тестируемого GPU без сжатия. Исходя из представления графа, 26 масштаб является последним, у которого количество ребер помещается в unsigned int, что является некоторым ограничением алгоритма для дальнейшего масштабирования. Данное ограничение легко обходится путем расширения типа данных. Как мне кажется, пока это не так актуально, так как обработка одинарной точности (unsigned int) осуществляется во много раз быстрее, чем двойной (unsigned long long) и количество памяти пока достаточно мало. Производительность будет измеряться в количестве обработанных ребер в секунду (traversed edges per second — TEPS). Компиляция осуществлялась с использованием NVidia CUDA Toolkit 7.0 с опциями -O3 -arch=sm_35, Intel Composer 2015 с опциями -O3. Максимальную производительность реализованного алгоритма можно увидеть на графике ниже: 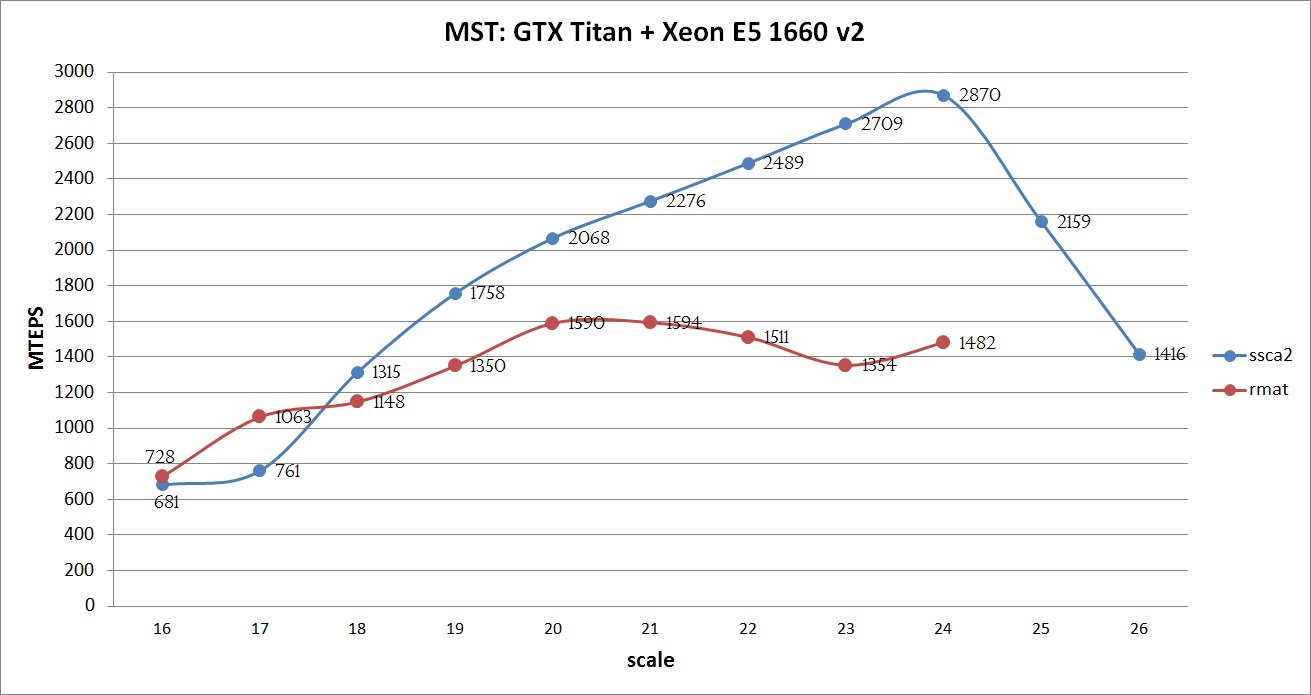 На графике видно, что с использованием всех оптимизаций SSCA2 графы показывают хорошую эффективность: чем больше граф, тем лучше производительность. Данный рост сохраняется до тех пор, пока все данные помещаются в память GPU. На 25 и 26 масштабах был использован механизм Unified Memory, который позволил получить результат, правда с более низкой скоростью (но как будет продемонстрировано ниже, быстрее, чем только на CPU). Если бы расчет выполняется на Tesla k40 с 12ГБ памяти и отключенным ECC и процессором Intel Xeon E5 V2/V3, то вполне возможно можно было бы достичь порядка 3000 MTEPS на графе SSCA2 масштаба 25, а также попытаться обработать не только граф 26го масштаба, но и 27. Для RMAT графа такой эксперимент не проводился, в силу его сложной структуры и плохой адаптации алгоритма. Сравнение производительности различных алгоритмов Данная задача решалась в рамках конкурса конференции GraphHPC 2015. Я бы хотел привести сравнение с программой, написанной Александром Дарьиным, который по мнению авторов занял первое место в данном конкурсе. Так как в общей таблице есть результаты на тестовой платформе, предоставленной авторами, то не лишним было бы привести графики на CPU и GPU на описанной платформе (GTX Titan + Xeon E5 v2). Ниже представлены результаты для двух графов: 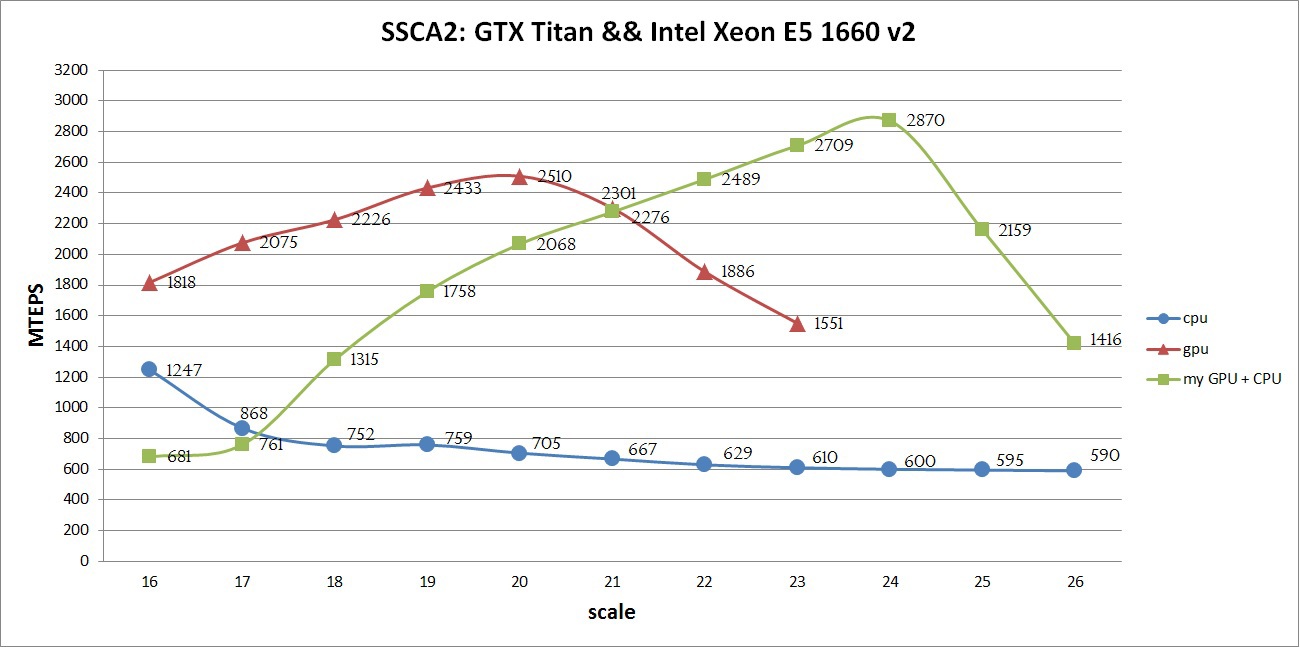 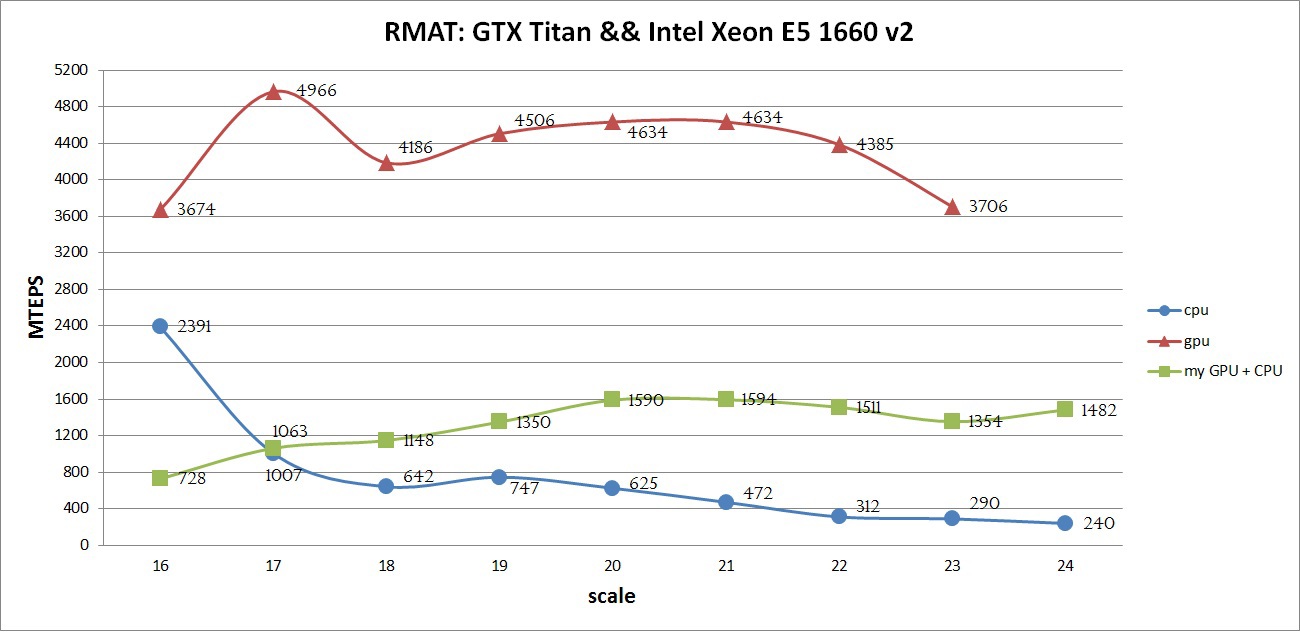 Из приведенных графиков видно, что описанный в данной статье алгоритм больше оптимизирован для SSCA2 графов, в то время как алгоритм, реализованный Александром Дарьиным, хорошо оптимизирован для RMAT графов. В данном случае нельзя сказать однозначно какая из реализаций является лучшей, потому что у каждой есть свои преимущества и недостатки. Также не ясен критерий, по которому надо оценивать алгоритмы. Если говорить про обработку больших графов, то тот факт, что алгоритм может обработать графы 24-26 масштаба, является большим плюсом и преимуществом. Если говорить о средней скорости обработки графов любой величины, то не ясно, какую именно среднюю величину считать. Ясно только одно — один алгоритм хорошо обрабатывает SSCA2 графы, второй — RMAT. Если объединить две эти реализации, то средняя производительность будет порядка 3200 MTEPS для 23 масштаба. Презентация описания некоторых оптимизаций алгоритма Александра Дарьина можно посмотреть здесь. Из зарубежных статей можно выделить следующие. 1) [13] Из данной статьи были использованы некоторые идеи при реализации описанного алгоритма. Напрямую сравнивать полученные авторами результаты нельзя, так как тестирование производилось на старой NVidia Tesla S1070. Достигнутая авторами производительность на GPU колеблется от 18-36 MTEPS. Опубликована в 2009 и в 2013 годах. 2) [14] реализация алгоритма Прима на GPU. 3) [15] реализация k NN-Boruvka на GPU. Также существуют некоторые параллельные реализации на CPU. Но высокой производительности в зарубежных статьях я так и не смог найти. Может кто-нибудь из читателей сможет подсказать, если я что-то упустил. Также стоит отметить, что в России публикаций по этой теме практически нет (за исключением Зайцева Вадима), что очень печально, как мне кажется. Список источников Айзерман М.А., Браверман Э.М., Глушков В.М. и др. Теория распознавания образов и обучающих систем. – Изв. АН СССР, Техническая кибернетика № 5, 1963, с. 98-101. Вайнцвайг М.Н. Алгоритм обучения распознавания образов «Кора». В сб.: Алгоритмы обучения распознавания образов. – М.: 1972, с. 110-116. Васильев В.И. Распознающие системы: Справочник. / В.И. Васильев – К.: Наукова думка, 1983. – 423 с. Загоруйко Н.Г. Прикладные методы анализа знаний и данных / Н.Г. Загоруйко. – Новосибирск: Издательство института математики, 1999. – 270 с. Волченко Е.В. Сеточный подход к построению взвешенных обучающих выборок w-объектов в адаптивных системах распознавания // Вісник Національного технічного університету «Харківський політехнічний інститут». Збірник наукових праць. Тематичний випуск: Інформатика i моделювання. – Харків: НТУ «ХПІ», 2011. – № 36. – С. 12-22. Волченко Е.В. Модифицированный метод потенциальных функций / Е.В. Волченко II Бионика интеллекта. – 2006. – № 1 (64). – С. 86-92. Волченко Е. В., Кузьменко И. Ю. Анализ методов нахождения выбросов в обучающих выборках / Харьковский Политехнический Институт // Материалы ХI Международной научно-технической конференции/ Секция «Молодые ученые«. – Харьков, ХПИ – 2011, , с. 12-13. Автореферат магистерской работы Шкарпеткина Ю.Г. «Исследование и разработка метода заполнения пропусков в взвешенных обучающих выборках данных» [Электронный ресурс]. – Режим доступа: http://masters.donntu.org/2012/iii/shkarpetkina/diss/index.htm Чубукова И.А. Data Mining. Учебное пособие. – М.: Интернет-Университет Информационных технологий; БИНОМ. Лаборатория знаний, 2006. – 382 с.: ил., табл. – (Серия «Основы информационных технологий») Паклин Н. «Кластеризация категорийных данных: масштабируемый алгоритм CLOPE». [Электронный ресурс]. – Режим доступа: http://www.basegroup.ru/clusterization/clope.htm Sudipto Guha, Rajeev Rastogi, Kyuseok Shim «CURE: An Efficient Clustering Algorithm for Large Databases». Proceedings of the 1998 ACM SIGMOD international conference on Management of data pp.. 73-84 Tian Zhang, Raghu Ramakrishnan, Miron Livny «BIRCH: An Efficient Data Clustering Method for Very Large Databases». Proceedings of the 1996 ACM SIGMOD international conference on Management of data pp. 103-114 Daniel Fasulo «An Analysis Of Recent Work on Clustering Algorithms». [Электронный ресурс]. – Режим доступа: http://logic.pdmi.ras.ru/ics/papers/aca.pdf Паклин Н. «Алгоритмы кластеризации на службе Data Mining». [Электронный ресурс]. – Режим доступа: http://www.basegroup.ru/clusterization/datamining.htm | ||||||||||||||||||||||||||||||||||||||||||||