лаба 7. лабораторная работа 7 тидз. Решение задачи регрессии с помощью нейронной сети
 Скачать 198.25 Kb.
|
|
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича» Кафедра «Информационных управляющих систем» Дисциплина «Теория информации, данные, знания» ОТЧЁТ по лабораторной работе № 7 ««Решение задачи регрессии с помощью нейронной сети»» Выполнили: студент группы ИСТ-031 Белослудцева Ирина «05» апреля 2022г. _________/______________/ Принял: старший преподаватель кафедры «___» ________ 2022 г. _________/А.М. Струев / Санкт-Петербург 2022 Цель работы – исследование принципов разработки нейронной сети на примере задачи регрессии. Задачи исследования: предсказать функцию sin (x) предсказать функцию y = 2x * sin(2−x) получить метрику MAE = 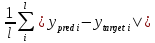 Результаты исследования (Вариант 6) В ходе предсказания функции sin (x) с помощью нейронной сети при начальных параметрах:
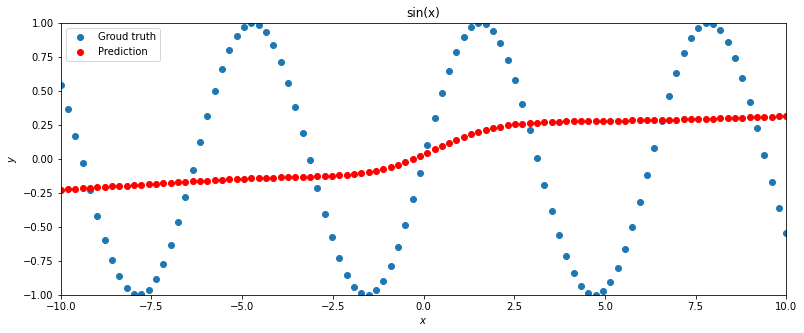 Получаем результат, который не соответствует необходимым требованиям. При смене метода оптимизации с SGD на ADAM и тех же значениях n_hidden_neurons и lrполучаем наиболее точный результат  Найдём минимальное значение n_hidden_neurons, при котором сеть будет давать удовлетворительные результаты. В ходе постепенного уменьшения значения n_hidden_neurons получаем, что n_hidden_neurons =13 - минимальное значение, при котором сеть дает удовлетворительные результаты, с учётом того, что используется метод оптимизации ADAM, так как метод оптимизации SGD не даёт хороших результатов ни при каких значениях. Путём исследования определяем, что 0,01 - наилучшее значение шага градиентного спуска lr в интервале 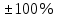 от номинального значения. 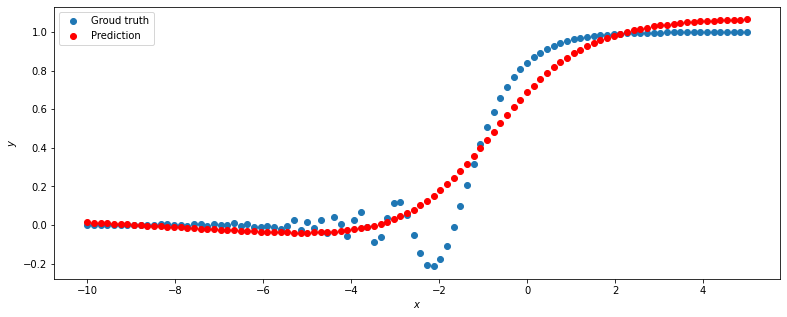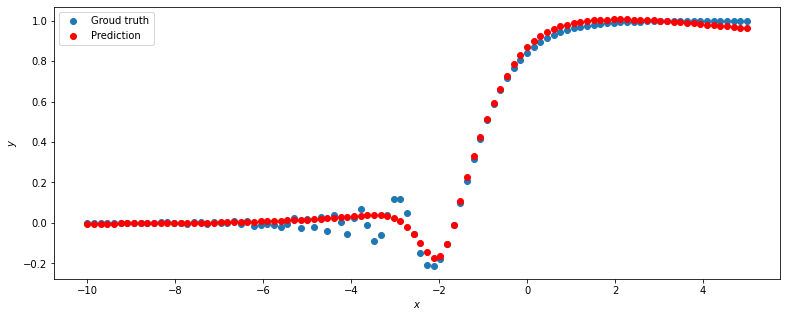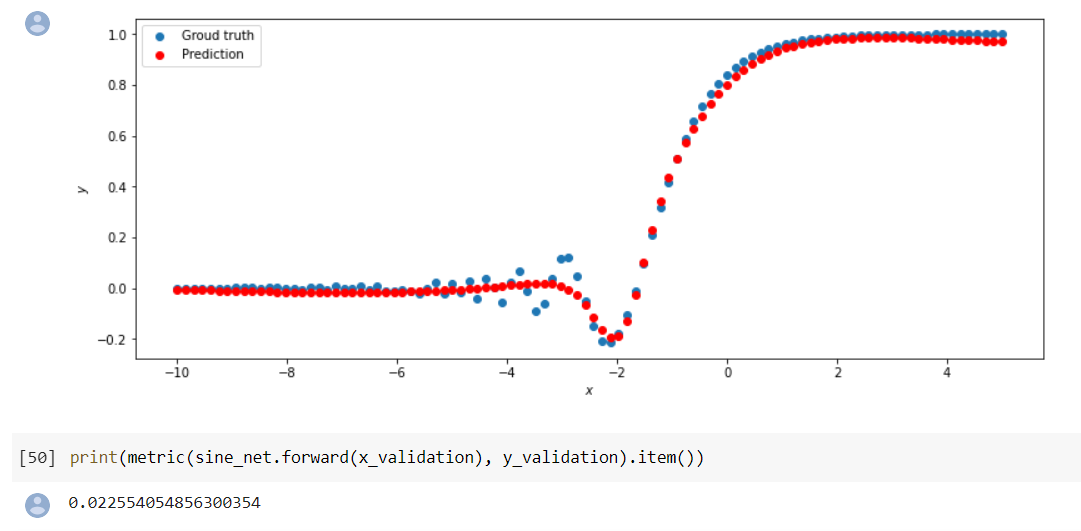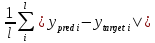(при (при n_hidden_neurons = 12) Меняем нейронную сеть для предсказания функции y = 2x * sin(2−x) Для получения лучшего результата изменяем метод оптимизации на ADAM  Чтобы вычислить метрику MAE = не хуже 0.03 нужно изменить метод оптимизации на ADAM, а значения n_hidden_neurons и lr оставляем прежними, то есть n_hidden_neurons = 20, lr = 0,01Вывод: Исследовав принципы разработки нейронной сети на примере задачи регрессии, я поняла, что метод оптимизации, количество нейронов и шаг градиентного спуска оказывают большое влияние на результат работы нейронной сети. |