ТФКП_контрольная работа. ЗАДАНИЯ. Решение Задание Представить комплексное число в тригонометрической форме Решение
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
Задание 1. Выполнить указанные действия: 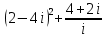 Решение: 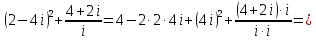 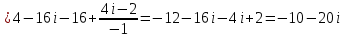 Задание 2. Представить комплексное число в тригонометрической форме: 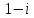 Решение: r=|z|= 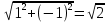 , тогда cosφ= , тогда cosφ=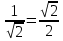 , sinφ= , sinφ=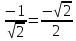 argz=φ= argz=φ=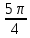 так получаем запись в тригонометрической форме: z1 = 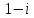 = = 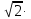 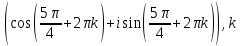 Z ZЗадание 3. Вычислить корень 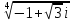 Решение: Представим комплексное число, являющееся подкоренным выражением, в тригонометрической форме: r=|z1|= 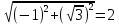 , тогда cosφ= , тогда cosφ=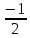 , sinφ= , sinφ=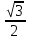 argz=φ= 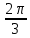 так получаем запись в тригонометрической форме: z1 = 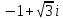 = = 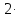 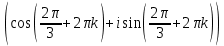 ) )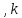 Z Zr=|z|= 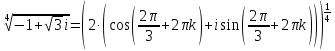 = =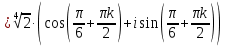 Задание 4. Представить число в показательной форме: 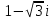 Решение: r=|z1|= 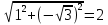 , тогда cosφ= , тогда cosφ=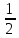 , sinφ= , sinφ=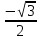 argz=φ= argz=φ=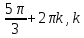 Z Zтак получаем запись в показательной форме: z1 = 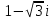 = = 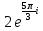 Задание 5. Определить и построить множество точек, удовлетворяющих данным уравнениям или неравенствам: 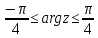 Решение: argz1= 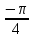 , argz2= , argz2=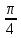 - границы области. - границы области.Данная область представляет собой часть плоскости, ограниченной двумя лучами, лежащими на прямых у=х и у=-х, с началом в т. (0; 0) 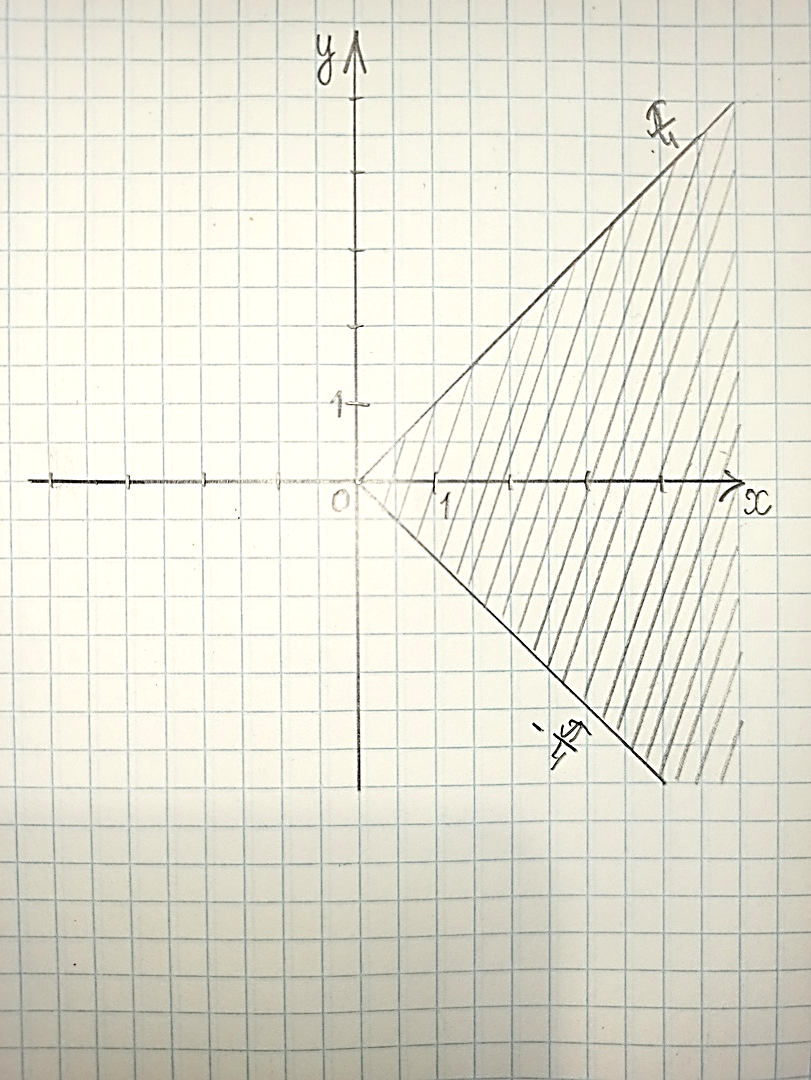 |
