Задания по химии с решением. Решение Закон гласит количества эквивалентов вступающих в реакцию веществ равны
 Скачать 64.02 Kb.
|
|
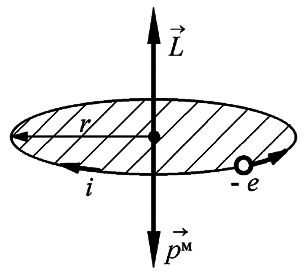
1. При восстановлении 1,17 г оксида олова водородом образовалось 0,16 г воды. Вычислите эквивалентную массу олова. Дано: 1,17 г оксида олова, 0,16 г воды Решение: Закон гласит: количества эквивалентов вступающих в реакцию веществ равны. 0.16г воды — это 0.16*16/18 = 0.1422 г кислорода Исходный оксид олова содержал 1.0278г олова и 0.1422г кислорода. Если атомная масса 118 г/моль, то фактор экв. равен 2, и формула оксида SnO. экв. масса кислорода = 8 г/(моль*экв) кол-во экв. кислорода 0.1422/8 = 0.017775 моль*экв. олова столько же, значит его экв. масса: 1.0278 / 0.017775 = 57.9 г / (моль*экв) Ответ: 57,9 г. 2. Объясните физический смысл орбитального квантового числа. Укажите значения, которые оно может принимать и формы орбиталей, которые им соответствуют. В квантовых состояниях с заданным значением главного квантового числа  азимутальное квантовое число может иметь следующие значения: .Из выводов предыдущего параграфа следует, что стационарные волновые функции  , описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии  , но и оператора квадрата момента импульса  , причем .Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
Проанализируем эту формулу квантования момента импульса. Сравнивая ее с условием квантования момента импульса движущегося электрона в теории Бора, можно заметить, что эти условия не совпадают. И дело не только в отличии числовых значений, рассчитанных по этим формулам. Принципиальное отличие этих соотношений состоит в том, что в квантовой механике возможны состояния атома с нулевым моментом импульса. Во всех  -состояниях и, частности, в основном  -состоянии, когда  , по формуле получаем  .При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса. Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем - таков вывод современной физики. Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно охарактеризовать орбитальным магнитным моментом  .В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса  со скоростью  , величина орбитального механического момента равна  . Если время полного оборота электрона  , то такому движению соответствует замкнутый ток ,который можно охарактеризовать величиной магнитного момента  .Связь механического и магнитного моментов при этом определяется гиромагнитным отношением
Так как заряд электрона отрицателен, то для орбитального движения направление вектора магнитного момента противоположно направлению вектора механического момента импульса  .Для расчета орбитального магнитного момента в квантовой теории следует определить пространственную плотность электрического тока  через плотность потока вероятностей  по формуле:  . Плотность потока вероятности при этом можно найти по формуле, зная волновую функцию электрона в заданном квантовом состоянии атома. Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле.
Итак, в любом квантовом состоянии атом водорода обладает не только механическим моментом  , величина которого определяется формулой, но и магнитным моментом.
Здесь универсальная постоянная 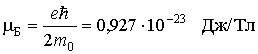 служит единицей измерения магнитных моментов атомов и называется магнетоном Бора. Если атом переходит из одного квантового состояния в другое с испусканием (поглощением) фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое число  изменяется на единицу. Это правило, согласно которому для оптических переходов  , называется правилом отбора. Наличие такого правила отбора обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.Физический смысл орбитального квантового числа l заключается в том, что оно определяет значение углового момента. Дискретность l определяет дискретные значения L, т.е. величина углового момента квантуется. Для состояния с l = 0 угловой момент равен нулю. 3. Укажите тип кристаллической решетки и характер связи в кристаллах NaCl и Na. Чему равно координационное число натрия в этих решетках? Натрий - элемент IA группы ПСХЭ Д.И. Менделеева, порядковый номер 11, имеет на внешнем энергетическом уровне 1 электрон, следовательно - типичный металл. Металлы могут образовывать всего 2 вида химической связи: а) Металлическая связь (для металлического натрия - простого вещества); б) Ионная химическая связь (в соединения с атомам элементов-неметаллов). Строение кристаллических решеток обусловлено видом химической связи. Для веществ с металлической связью образуется металлическая кристаллическая решетка (в узлах КР находятся атом-ионы натрия, а между ними располагаются делокализованные общие электроны, принадлежащие сразу всем атом-ионам - электронный газ). В случае металлического натрия кристаллическая решетка кубическая гранецентрированная. Вещества с ионной химической связью обладают ионной кристаллической решеткой (в узлах находятся ионы Na+ и Cl-, при этом они чередуются между собой через один). Тип кристаллической решетки в этом случае кубическая. Таким образом один атом натрия в обоих случаях координирует 8 соседних частиц. Значит, координационное число натрия равно 8. 4. Определить, на сколько градусов необходимо повысить температуру, чтобы скорость реакции увеличилась в 27 раз (температурный коэффициент (γ) равен 3). Дано: скорость реакции увеличилась в 27 раз (γ) = 3 Решение: По правилу Вант-Гоффа имеем V2/V1 = гамма^ (t2-t1)/10 V2/V1 - отношение скоростей реакций при температурах t2 и t1 (по условию 27) А гамма - температурный коэффициент(по условию 3) 27= 3^(t2-t1)/10 (t2-t1)/10 = 3 t2-t1 = 30 Ответ: на 30 градусов 5. Вычислите энергию Гиббса тепловой денатурации трипсина при 50о С, если при 25оС ∆Н0реакции= 283 кДж/моль, а ∆S0 реакции =288 Дж/(моль·К). Считать, что изменение энтальпии и энтропии не зависит от температуры в данном диапазоне. Дано: ∆Н0реакции= 283 кДж/моль ∆S0 реакции =288 Дж/(моль·К) Решение:  283 кДж/моль – 323 К ∙ 288 · 103 кДж/моль ∙ K = 190 кДж/моль.Обратите внимание, что T · ΔS° = 323 ∙ 288 ∙ 10–3 = 93,024 кДж/моль, то есть ΔН° > T · ΔS° Ответ: > 0, реакция эндэргоническая за счет энтальпийного фактора. Реакция не может самопроизвольно протекать при данной температуре. 6. Рассчитайте объем раствора с массовой долей карбоната натрия 15% (g=1,16 г/см3), необходимый для приготовления 120 мл 0,45 М раствора Na2СО3. Дано: Доля карбоната натрия 15% (g=1,16 г/см3) 120 мл 0,45 М раствора Na2СО3. 1. Вычислим количество вещества Na2CO3 в 0,45М растворе объемом 120 мл: n(Na2CO3)= C(Na2CO3) ⋅ V(р-ра) = 0,45⋅ 0,12= 0,054 моль 2. Масса вещества составит: m(Na2CO3)= n(Na2CO3) M(Na2CO3)= 0,054 ·106 = 5,72 г 3. Вычислим массу раствора с массовой долей Na2CO3 0,15 mр—ра (Na2CO3)= m(Na2CO3)\ω(Na2CO3)=5,72\0,15 = 38,13 г 4. Vр—ра(Na2CO3)= mр—ра (Na2CO3)\ρр—ра(Na2CO3) = 38,13\1,16 = 32,8 мл Ответ: 32,8 мл 7. В желудке содержится соляная кислота, которая практически полностью диссоциирует в водных растворах. Рассчитайте рН желудочного сока, если массовая доля HCl в нем составляет в норме 0,05%. Плотность желудочного сока принять равной 1 г/см3. Дано: 0,05 % HCl в 100 г жел. сока. Решение: n(HCl)=m/M=0,5/36,5=0,014 моль при плотности жел. сока=1, мол. концентрация С (HCl)=n/V=0,014/0,1=0,14 моль/л HCl=H+ + Cl+ [H+]=C=0,14 моль/л pH=-lg[H+]=0,86 Ответ: 0,86 8. Запишите уравнение Гендерсона-Хасельбаха для расчета рН фосфатной и гидрокарбонатной буферной системы. Формула для расчета рН буферного раствора: рН = рК о + lg C о /С с Это уравнение Гендерсона – Хассельбаха. Для фосфатной буферной системы HPO42-/H2PO4- pH можно рассчитать по уравнению: 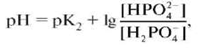 где K2 - константа диссоциации ортофосфорной кислоты по второй ступени. к гидрокарбонатной буферной системе (уравнение Гендерсона-Гассельбаха) имеет следующий вид: рН = 6,1 + lg ; рН = 6,1 + lg. где s´ -коэффициент растворимости СО2 в воде при парциальном давлении 101 кПа. 9. Имеются два раствора хлорида кальция и хлорида натрия с одинаковой процентной концентрацией 0,85% и одинаковой плотностью 1 г\мл при температуре 310 К. Будут ли эти растворы изотоничны по отношению друг к другу? Дано: хлорид натрия – 0,85% Плотность - 1 г/мл С-310 К. Решение: Моляльная концентрация соли в растворе равна:
сm (ZnCl2) = 0,85 г/136 г/моль 0,125 кг = 0,05 моль/кг; По закону Рауля понижение температуры кристаллизации без учета диссоциации электролита составляет: Ткр = Kкр сm = 1,86 град/кг моль 0,05 моль/кг = 0,093 град. Сравнивая найденное значение с экспериментально определенным понижением температуры кристаллизации, определяем изотонический коэффициент i: i = Ткр.эксп. / Ткр.выч. = 0,23/0,093 = 2,47. Зная изотонический коэффициент, можно найти кажущуюся степень диссоциации соли:
Ответ: = 0,735 10. Составьте ионные и молекулярные уравнения реакции гидролиза CH3COONH4 и рассчитайте Kг. (KдNH4OH = 1,8·10–5, KдCH3COOH=1,8·10–5). CH3COONH4 + HOH = NH4OH + CH3COOH CH3COO(-) + NH4(+) + HOH = NH4(+) + OH(-) + CH3COO(-) + H(+) NH4(+) + HOH = NH4(+) + H(+) + OH(-) CH3COONH4+ HOH ↔ NH4OH + CH3COOH. КД (NH4OH) = 1,8 · 10-5 рК = -ℓg КД = - ℓg 1,8 · 10-5 = -(ℓg 1,8 - ℓg 10-5) = -0,26 = 5 = 4,74. Определяем интервал буферного действия по формуле: рОН = рК ± 1. рОН = 4, 74 ± 1; рН = 3,74 -5,74. Ответ: значение рОН = 4,74 входит в интервал рК 3,74 – 5,74, поэтому такой аммиачный буфер можно приготовить. 11. Используя электронно-ионный метод, определите стехиометрические коэффициенты методом в следующей ОВР: Н2S + K2Cr2O7 + H2SO4 → S + Cr2(SO4)3 + K2SO4 + H2O Уравнения полуреакций выгляд так(в скобках степени окисления): S(2-)-2e = S(0), Cr2O7(2-)+14H(1+) +6e=2Cr(3+) + 7H2O. Т. о. коэффицент для серы 3. Полное уравнение: 3H2S+K2Cr2O7+4H2SO4 = 3S+Cr2(SO4)3+K2SO4+7H2O 12. Вычислите ЭДС марганцево-никелевого гальванического элемента (–)Мn/MnSO4׀׀NiSO4/Ni(+), если образующие его электроды опущены в растворы солей с одинаковой активностью катиона (Е0Mn/Мn2+ = – 1,05 B, Е0Ni/Ni 2+= –0,23 В). Mn | Mn+2 || Ni+2| Ni Ео (Mn(2+)/Mn) = − 1,18 В Ео (Ni(2+)/Ni) = − 0,25 B Поскольку в схеме гальванического элемента слева записывается анод, а справа – катод, то в данном гальваническом элементе анодом является алюминиевый электрод, а катодом – цинковый. В гальваническом элементе анодом становится металл, обладающего меньшим значением электродного потенциала, а катодом – металл с большим значением электродного потенциала. Поскольку марганец в ряду стандартных электродных потенциалов (электрохимическом ряду напряжений) стоит левее никеля, следовательно, марганец имеет меньший стандартный электродный потенциал восстановления, чем никель. Значит, в гальваническом элементе марганцевый электрод будет анодом, а никелевый – катодом. На аноде протекает процесс окисления, а на катоде – процесс восстановления. Процессы окисления-восстановления на электродах. Анод (-) Mn(0) – 2е = Mn(2+) | 1 – окисление на аноде Катод (+) Ni(2+) + 2e = Ni(0) | 1 – восстановление на катоде Суммируя реакции на аноде и катоде, получаем уравнение токообразующей реакции, которое в ионной форме, выражает происходящую в элементе реакцию. Mn + Ni(2+) → Mn(2+) + Ni Стандартная ЭДС гальванического элемента. ЭДСо = Ео (катода) – Ео (анода) = Ео (Ni(2+)/Ni) - Ео (Mn(2+)/Mn) = − 0,25 − (− 1,18) = 0,93 В Стандартная ЭДС гальванического элемента соответствует молярной концентрации ионов Mn(2+) и Ni(2+) в растворах электролитов равной 1моль/л. Список используемой литературы 1. https://ru.wikipedia.org/wiki/Оксид_меди(II) 2. https://studfile.net/preview/5364605/page:4/ 3. https://infopedia.su/13x4f13.html | ||||||||||||||||||||||||||||||||||||||||||
.
.
.
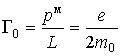