Решение Заменим опоры реакциями связи и изобразим эквивалентную схему нагружения

• Название: Решение Заменим опоры реакциями связи и изобразим эквивалентную схему нагружения
• Дата: 25.02.2022
• Размер: 487.81 Kb.
• Имя файла: Mekh_idz_1_melnik_V_a_5b03.docx
• Тип: Документы; #372948

Министерство НАУКИ И ВЫСШЕГО образования Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»


Школа базовой инженерной подготовки

Отделение общетехнических дисциплин

«Определение реакции опор плоской конструкции»
Индивидуальное задание № 1

Вариант - 10

по дисциплине:

МЕХАНИКА
Исполнитель:

Студент группы 5Б03 Мельник В.А. 19.09.21

Руководитель:

Преподаватель канд. физ. мат. наук Коноваленко И.С.


Томск – 2021

Техническая задача:

Стальная стержневая конструкция находится под действием сил, моментов и распределенной нагрузки. Определить реакции опор твердого тела. Сделать проверку. Длины участков заданы в метрах.

Индивидуальный шифр – 4 1 0 1 0.

Дано:

P₁ = 18 кН;

P₂ = 16 кН;

P₃ = 10 кН;

G = 14 кН;

q = 4 кН/м;

M = 4 кН·м;

Углы α = 45° и β=30°.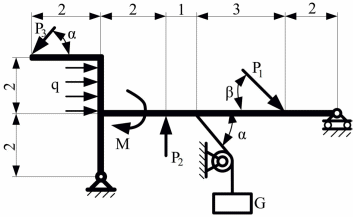



Рис. 1. Схема нагружения плоской конструкции


Решение:

Заменим опоры реакциями связи и изобразим эквивалентную схему нагружения.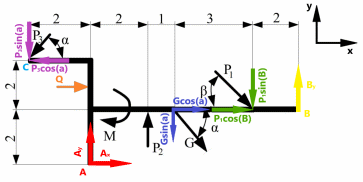


Рис.2 Эквивалентная схема нагружения

Для определения реакций запишем уравнения равновесия:

Q = 2·q = 8 кН

∑M_A = P₃·sin(α)·2 + P₃·cos(α)·4 – Q·3 – M + P₂·2 – G·sin(α)·3 – G·cos(α)·2 – P₁·cos(β)·2 – P₁·sin(β)·6 + B_y·8 = 0 (1)

∑M_B = P₃·sin(α)·10 + P₃·cos(α)·2 – Q·1 – M – P₂·6 + G·sin(α)·5 + P₁·sin(β)·2 – A_y·8 + A_x·2 = 0 (2)

∑F_ix = -P₃·cos(α) + Q + A_x + G·cos(α) + P₁·cos(β) = 0 (3)

Из (1) найдем B_y:

P₃·sin(α)·2 + P₃·cos(α)·4 – Q·3 – M + P₂·2 – G·sin(α)·3 – G·cos(α)·2 – P₁·cos(β)·2 – P₁·sin(β)·6 = -B_y·8

10·0,71·2 + 10·0,71·4 – 8·3 – 4 + 16·2 – 14·0,71·3 – 14·0,71·2 – 18·0,87·2 – 18·0,5·6 = - B_y·8

-88,42 кН = - B_y·8

B_y = 11,05 кН

Из (3) найдем A_x:

A_x = P₃·cos(α) - Q - G·cos(α) - P₁·cos(β)

A_x = 10·0,71 - 8 - 14·0,71 - 18·0,87

A_x = -26,5 кН

Из (2) найдем A_y:

A_y·8 = P₃·sin(α)·10 + P₃·cos(α)·2 – Q·1 – M – P₂·6 + G·sin(α)·5 + P₁·sin(β)·2 + A_x·2

A_y·8 = 10·0,71·10 + 10·0,71·2 – 8·1 – 4 – 16·6 + 14·0,71·5 + 18·0,5·2 + (-26,5)·2

A_y·8 = -8,1 кН

A_y = -1,01 кН
Проверка:

∑M_С = Q·1 + A_y·2 + A_x·4 – M + P₂·4 – G·sin(α)·5 + G·cos(α)·2 + P₁·cos(β)·2 – P₁·sin(β)·8 + B_y·10 = 0

8·1 + (-1,01)·2 + (-26,5)·4 – 4 + 16·4 – 14·0,71·5 + 14·0,71·2 + 18·0,87·2 – 18·0,5·8 + 11,05·10 = 0

-0,02 ≠ 0

Δ = (|-0,02|/110,5) · 100% = 0,0181%
Ответ: B_y = 11,05 кН

A_x = -26,5 кН

A_y = -1,01 кН

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОПОРАХ СОСТАВНОЙ КОНСТРУКЦИИ

Определить реакции опор и давление в промежуточном шарнире C заданной

составной конструкции, находящейся под действием внешних сил. Сделать

проверку.
Исходные данные: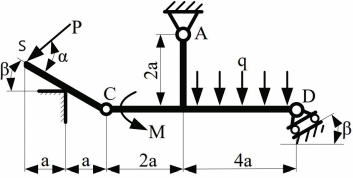



Рис.3 Составная конструкция
Сосредоточенная сила P =18 кН;

Распределенная нагрузка q=3 кН/м;

Сосредоточенный момент М=6 кНм;

Углы наклона α = 35° и β = 40°;

Длина a = 2 м.
Решение:
Данная конструкция состоит из двух тел, сочлененных шарниром C. Мысленно освобождаемся от связей, наложенных на каждое из тел, заменяя их на соответствующие реакции. Рассматриваем системы уравновешивающихся сил, приложенных к каждому телу в отдельности.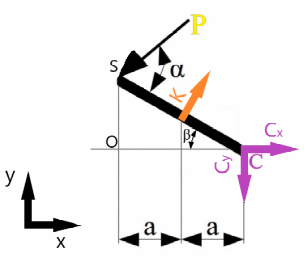



Рис. 4.1А. Эквивалентная схема нагружения левой части составной конструкции;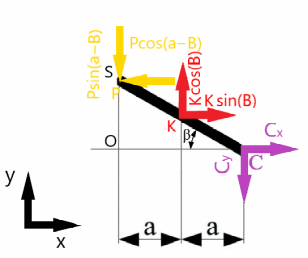


Рис. 4.1Б. Эквивалентная схема нагружения левой части составной конструкции;
Рассмотрим левую часть конструкции рис.4.1Б.

Для определения реакций составим уравнения равновесия:
∑M_С = P·sin(α-β)·2·a + P·cos(α-β)·2·a·tg(β) – K·cos(β)·a - K·sin(β)·a·tg(β) = 0

(1)

∑M_K = P·sin(α-β)·a + P·cos(α-β)·a·tg(β) + C_x·a·tg(β) – C_y·a = 0

(2)

∑F_ix = -P·cos(α-β) + K·sin(β) + C_x = 0

(3)

Из (1) найдем K:

P·sin(α-β)·2·a + P·cos(α-β)·2·a·tg(β) = K·cos(β)·a + K·sin(β)·a·tg(β)

P·sin(α-β)·2·a + P·cos(α-β)·2·a·tg(β) = K·(cos(β)·a + sin(β)·a·tg(β))

(P·sin(α-β)·2·a + P·cos(α-β)·2·a·tg(β))/(cos(β)·a + sin(β)·a·tg(β)) = K

(18·sin((-5)°)·2·2 + 18·cos((-5)°)·2·2·tg(40°))/(cos(40°)·2 + sin(40°)·2·tg(40°)) = K

20,42 кН = K

Из (3) найдем C_x:

-P·cos(α-β) + K·sin(β) = -C_x

(-18·cos((-5)°) + 20,42·sin(40°) = -C_x

-4,75 кН = -C_x

4,75 кН = C_x

Из (2) найдем C_y:

P·sin(α-β)·a + P·cos(α-β)·a·tg(β) + C_x·a·tg(β) – C_y·a = 0

P·sin(α-β)·a + P·cos(α-β)·a·tg(β) + C_x·a·tg(β) = C_y·a

18·sin((-5)°)·2 + 18·cos((-5)°)·2·tg(40°) + 4,75·2·tg(40°) = C_y·2

34,68 = C_y·2

17,34 кН = C_y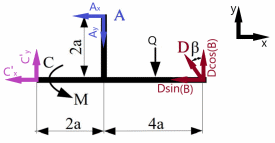



Рис. 4.2. Эквивалентная схема нагружения правой части составной конструкции;
Рассмотрим левую часть конструкции рис. 4.2.
Для определения реакций составим уравнения равновесия:
∑M_С = M + A_x·2·a – A_y·2·a – Q·4·a + D·cos(β)·6·a = 0

(4)

∑M_A = -Cꞌ_x·2·a– Cꞌ_y·2·a + M – Q·2·a - D·sin(β)·2·a + D·cos(β)·4·a = 0

(5)

∑F_jy = Cꞌ_y – A_y – Q + D·cos(β) = 0

(6)

Q = q·4·a = 3·4·2 = 24 кН

C_x = Cꞌ_x

C_y = Cꞌ_y
Из (5) найдем D:

-Cꞌ_x·2·a– Cꞌ_y·2·a + M – Q·2·a = D·sin(β)·2·a - D·cos(β)·4·a

-Cꞌ_x·2·a– Cꞌ_y·2·a + M – Q·2·a = D·(sin(β)·2·a - cos(β)·4·a)

(-Cꞌ_x·2·a– Cꞌ_y·2·a + M – Q·2·a)/(sin(β)·2·a - cos(β)·4·a) = D

(-4,75·2·2– 17,34·2·2 + 6 – 24·2·2)/(sin(40°)·2·2 - cos(40°)·4·2 = D

49.5 кН = D

Из (6) найдем A_y:

Cꞌ_y – Q + D·cos(β) = A_y

17,34 – 24 + 49,5·cos(40°) = A_y

31,5 кН = A_y

Из (4) найдем A_x:

M – A_y·2·a – Q·4·a + D·cos(β)·6·a = -A_x·2·a

6 – 31,5·2·2 – 24·4·2 + 49,5·cos(40°)·6·2 = -A_x·4

145,38 = -A_x·4

-36,35 кН = A_x

Проверка:

∑M_S = K·cos(β)·a + K·sin(β)·a·tg(β) + M + A_x· (2·a-2·a·tg(β)) – A_y·4·a – Q·6·a – D·sin(β)·2a·tg(β) + D·cos(β)·8·a = 0

20,42·cos(40°)·2 + 20,42·sin(40°)·2·tg(40°) + 6 + (-36,35)· (2·2-2·2·tg(40°)) – 31,5·4·2 – 24·6·2 – 49,5·sin(40°)·2·2·tg(40°) + 49,5·cos(40°)·8·2 = 0

-103,43=0

Δ = (|-103,43|/-669,71) · 100% = 15% (не знаю почему не сошлось, по решению ошибок не увидел)

Ответ: A_x = -36,35 кН

A_y = 31,5 кН

D = 49.5 кН

C_y = 17,34 кН

C_x = 4,75 кН