задача на теорему о движении центра масс механической системы. Практическая работа №3 (5). Решение Запишем исходное уравнение. В начальный момент времени, то есть, значит
 Скачать 383.66 Kb.
|
|
Вариант 7 С 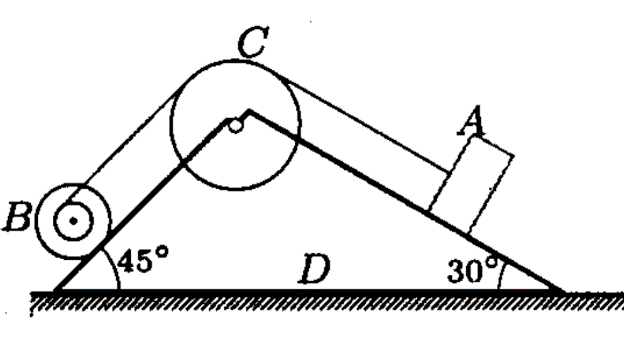 хема задачи приведена на рис.1. Дано:  ; ; ; см; ; см; ; .Определить:  и в тот момент времени, когда тело А пройдет расстояние м.Решение: 1. Запишем исходное уравнение  .В начальный момент времени  , то есть , значит .2. Вычисляем кинетическую энергию системы. Она равна сумме кинетических энергий отдельных тел:  .Здесь: Тело А совершает поступательное движение  .Так как  , то .Тело В совершает вращательное движение  .Так как 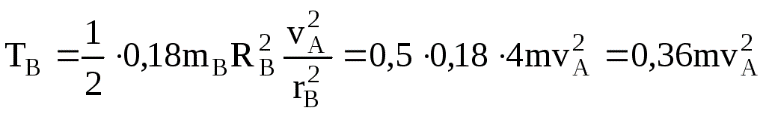 , и  , то .Тело Dсовершает плоскопараллельное движение  .Здесь 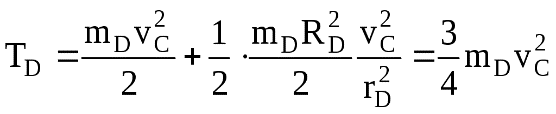 , а  , значит .Скорость точки С надо выразить через скорость точки А. Последовательно преобразовывая находим,  ; ; ; .Подставим известные значения  .Следовательно (при  ) находим .Таким образом  .3. Вычисляем сумму работ всех внешних сил 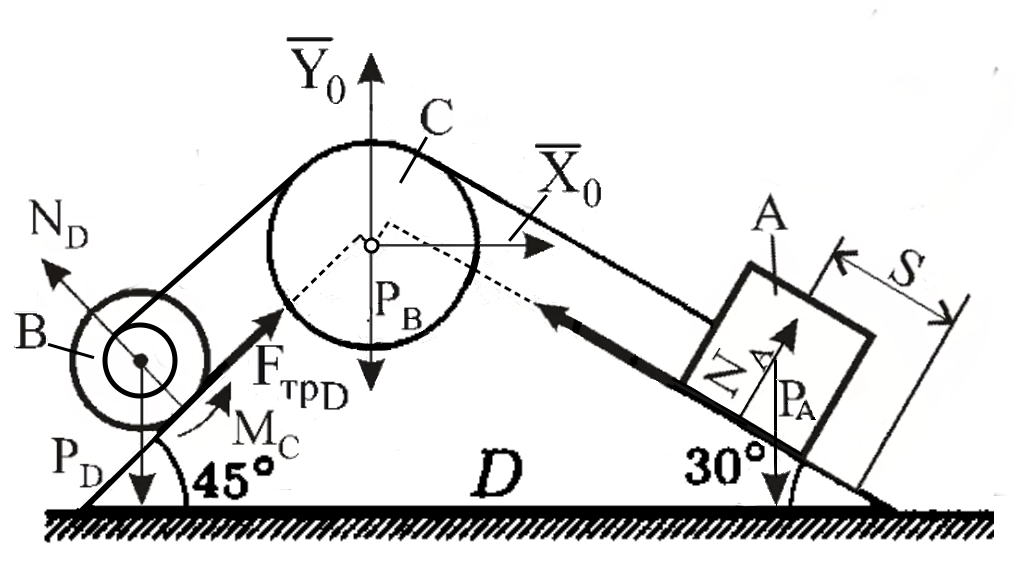 Рис.2. Изобразим еще раз схему, показанную на рис.1, и обозначим ее как рис.2. Приложим ко всем телам внешние активные силы и реакции связей. При движении тела А работу совершают только силы тяжести тел А и D: силы трения, приложенные к телу А:  и момент сопротивления качению, действующий на тело: .Остальные силы (  , , , , , ) работу не производят, так линии действия их перпендикулярны к скоростям движения соответствующих сил, или они приложены к неподвижным точкам, или (для силы ) – к мгновенному центру скоростей.Работу следует вычислять до 4 знака после запятой. Таким образом имеем  ,где:  ;  ;(т.к. 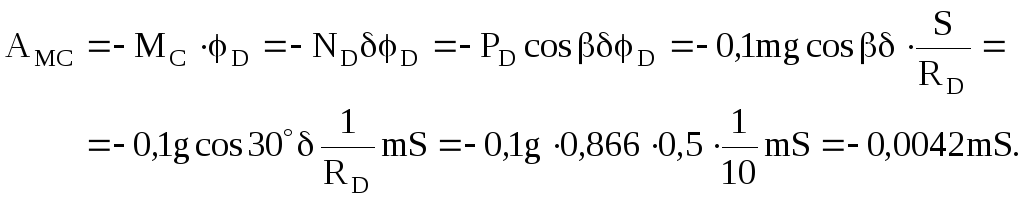 , то аналогично, ). Подставляя все значения, находим  .4. Определяем скорость и ускорение тела А. Приравняем  и : . (а)Отсюда, подставляя  м, находим м/с.Для определения ускорений надо взять от уравнения (а) (сокращая его на m) производную по времени  .Следовательно  м/с2. |