Лекция 3 СЛУ Метод Крамера. Решением слу называется упорядоченный набор значений неизвестных
 Скачать 291 Kb.
|
|
Лекция 3. Системы линейных уравнений. метод Крамера Содержание
1. Основные определения
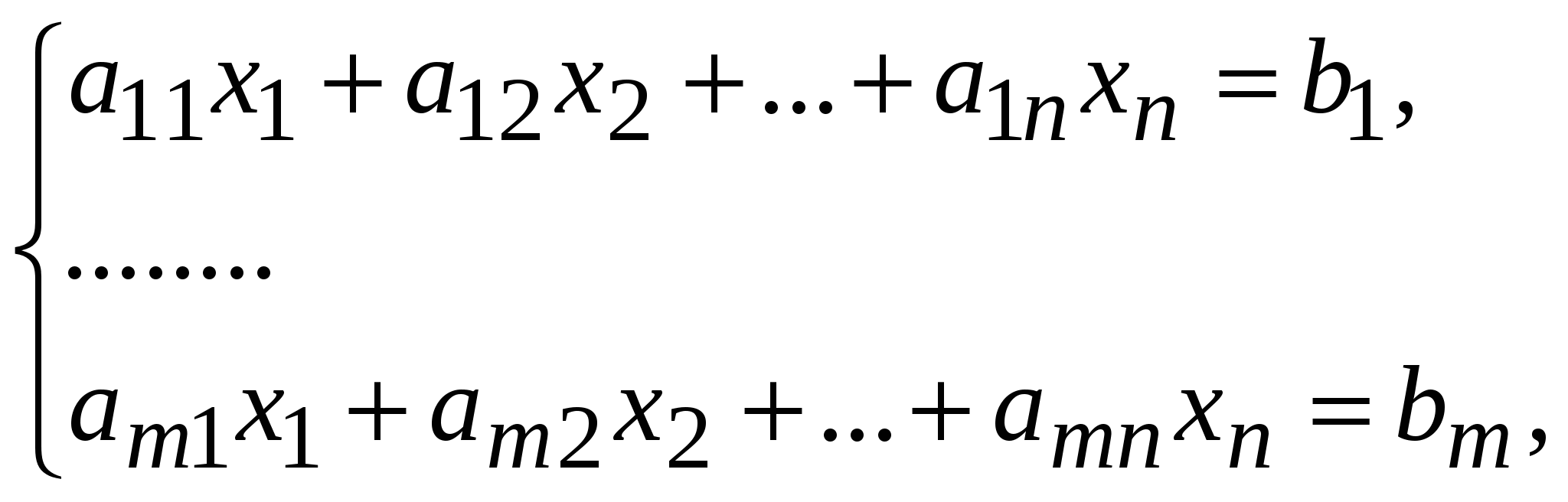 где числа  - коэффициенты при неизвестных,  - номер уравнения,  - номер неизвестной,  - свободные члены.
 ,который при подстановке в каждое уравнение системы вместо неизвестных соответственно  обращает их в верные равенства.
Система линейных уравнений называется: а) совместной, если она имеет хотя бы одно решение; б) несовместной, если она не имеет решений; в) определенной, если она имеет единственное решение; г) неопределенной, если она имеет бесконечное множество решений; д) однородной, если все свободные члены равны нулю  ; е) неоднородной, если есть  .2. Метод Крамера (определителей) решения систем линейных уравнений Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители. 2.1. Число уравнений и неизвестных равно 2 Рассмотрим систему линейных уравнений 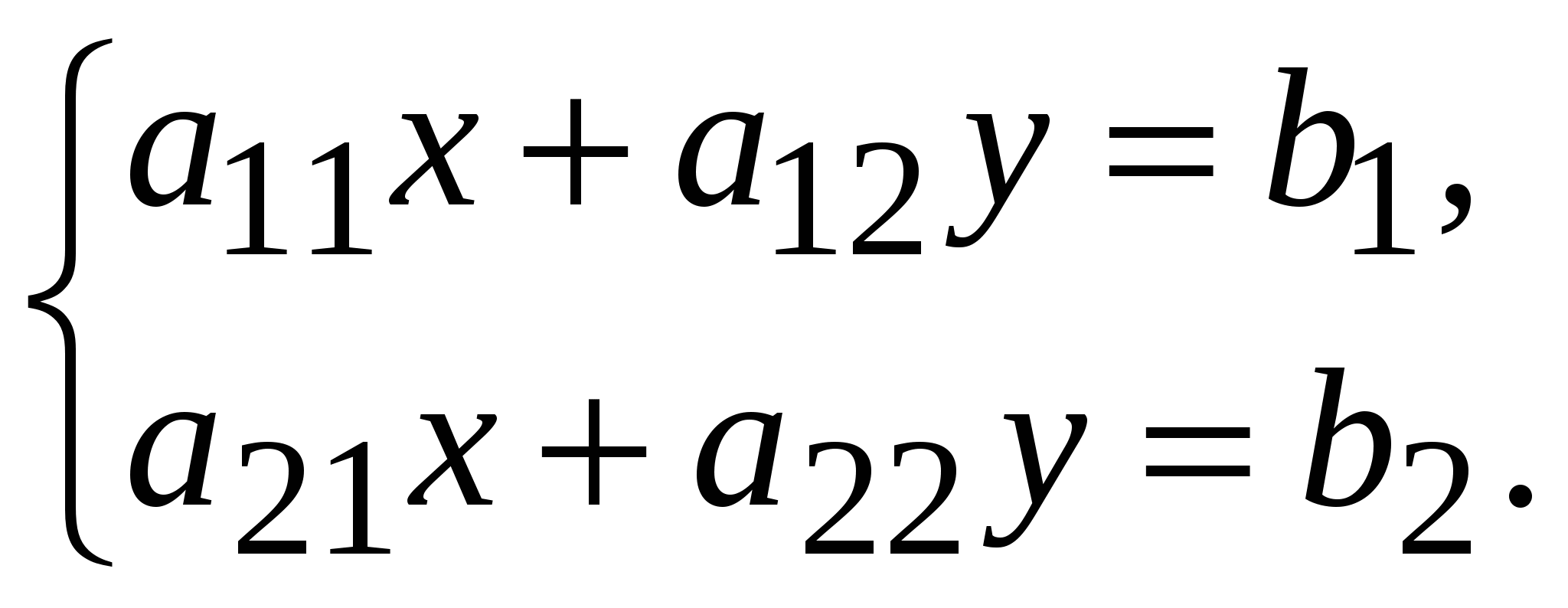 Вычисляются определители:  ,  ,  . Здесь - определитель системы, составленный из коэффициентов при неизвестных; - это определитель, полученный из определителя  заменой столбца коэффициентов при  на столбец свободных членов; - это определитель, полученный из определителя заменой столбца коэффициентов при  на столбец свободных членов.1. Если  , то система совместная и определенная, то есть имеет единственное решение, которое находится по формулам Крамера:   .2. Если  , а хотя бы один из определителей  ,  отличен от нуля, то система не имеет решений (несовместная). 3. Если  , то система имеет бесконечно много решений (совместная и неопределенная). Пример 1. Решить с помощью метода Крамера систему уравнений 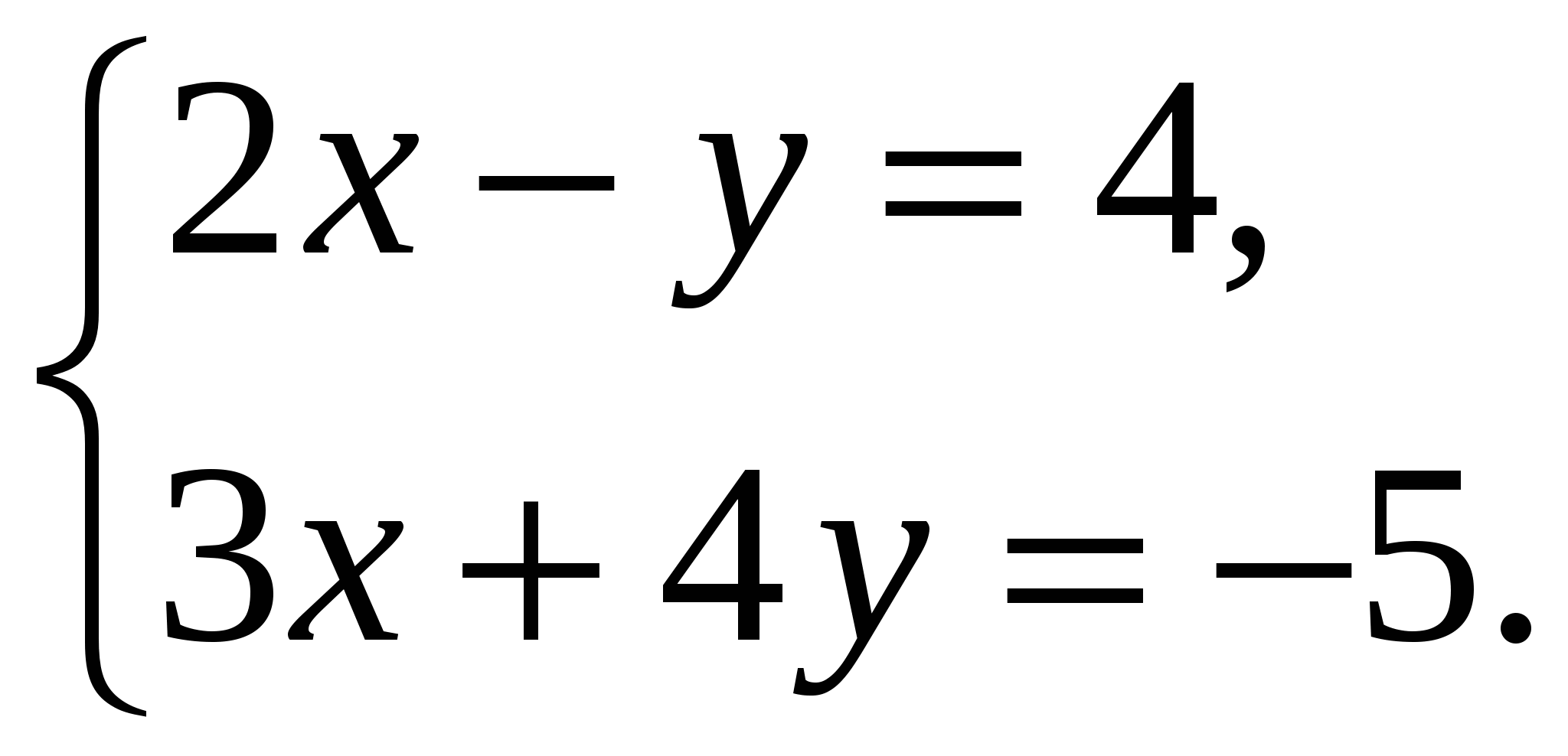 Решение  , поэтому СЛУ имеет единственное решение.  ,  .Тогда  ;  .Ответ: система уравнений совместна и определенна, ее единственное решение  .Пример 2. Решить с помощью метода Крамера систему уравнений 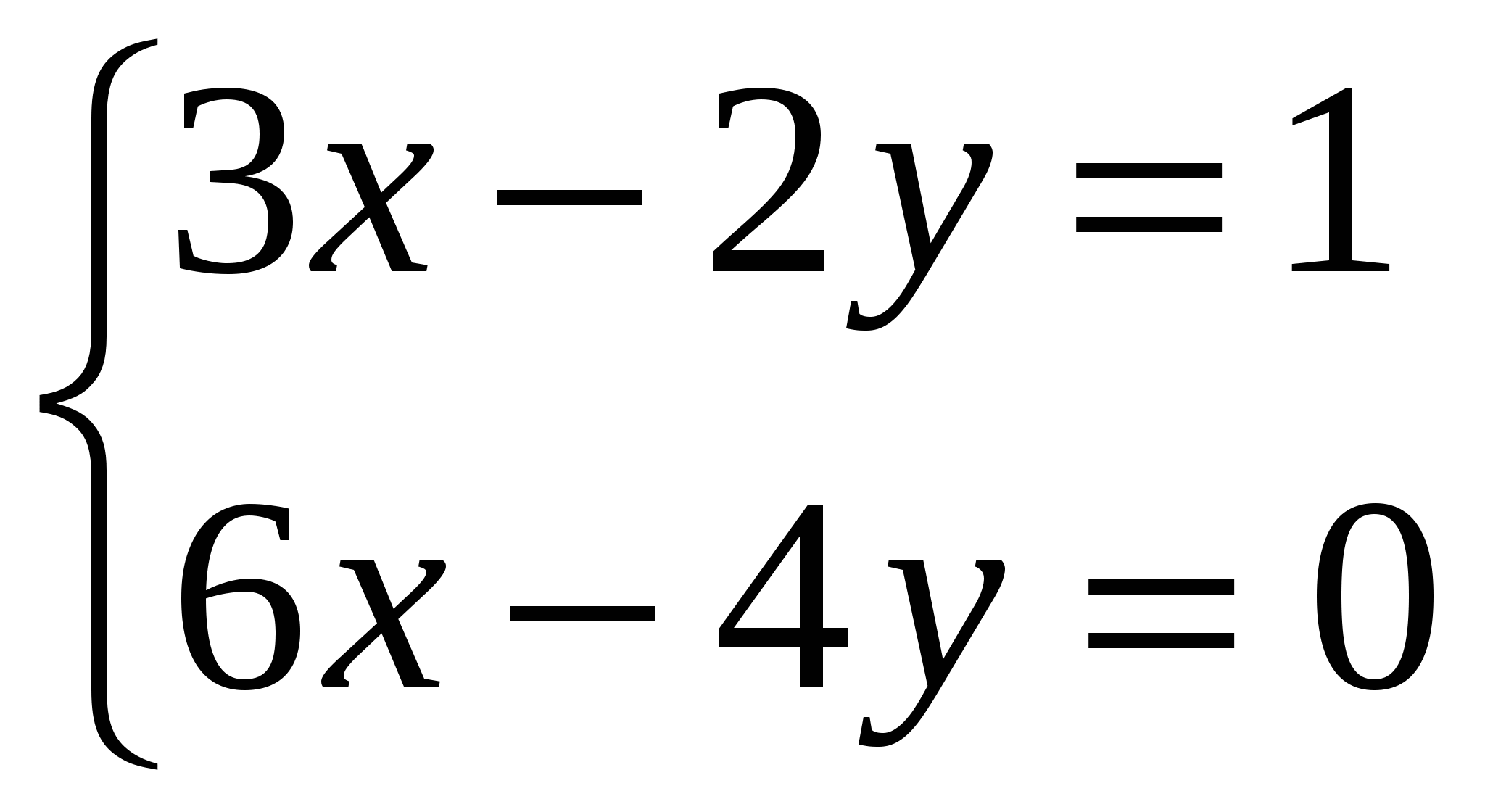 .Решение Определитель системы равен нулю:  , однако один из вспомогательных определителей не равен нулю:  , значит, СЛУ не имеет решений, то есть СЛУ несовместная. Пример 3. Решить с помощью метода Крамера систему уравнений 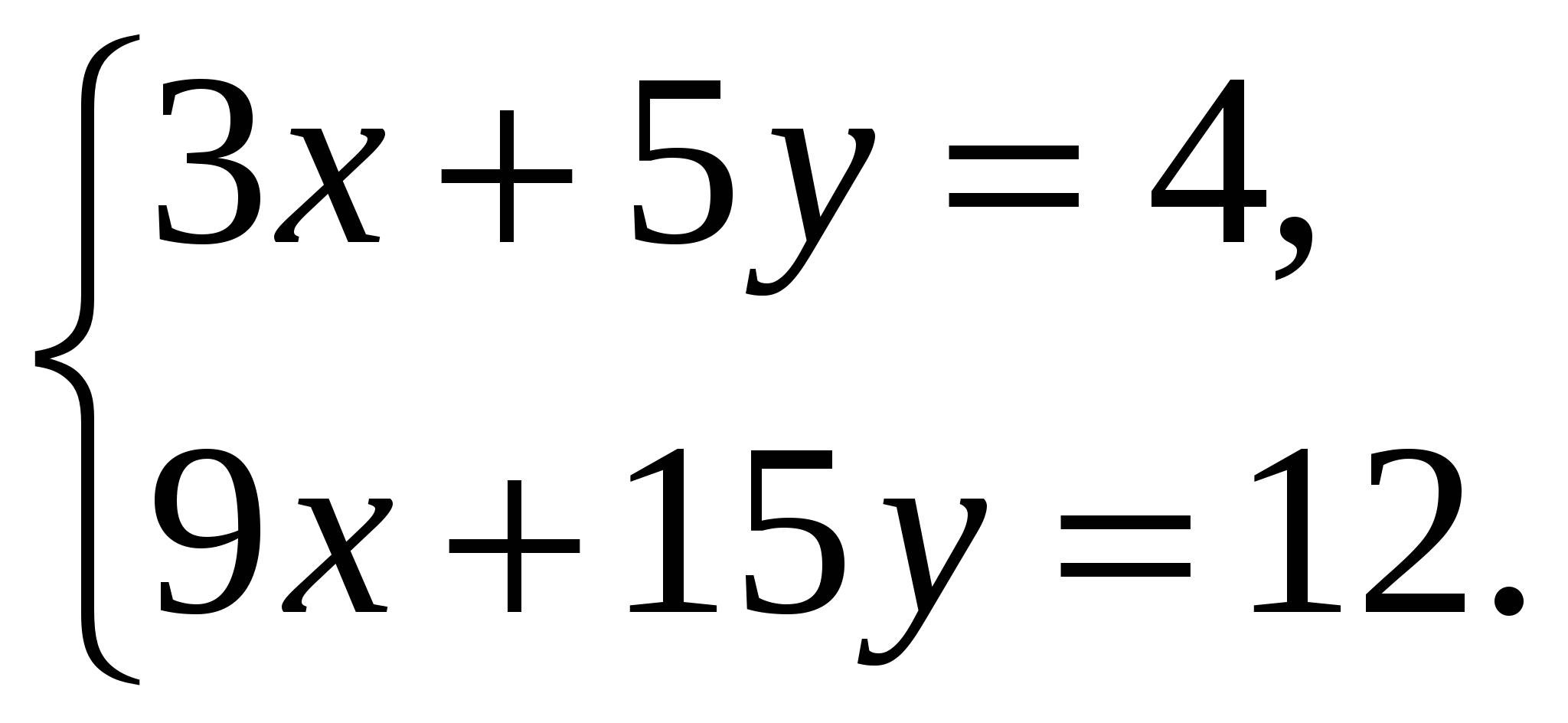 Решение  ,  ,  . Поэтому система имеет бесконечно много решений. Разделив коэффициенты 2-го уравнения на 3, получим: 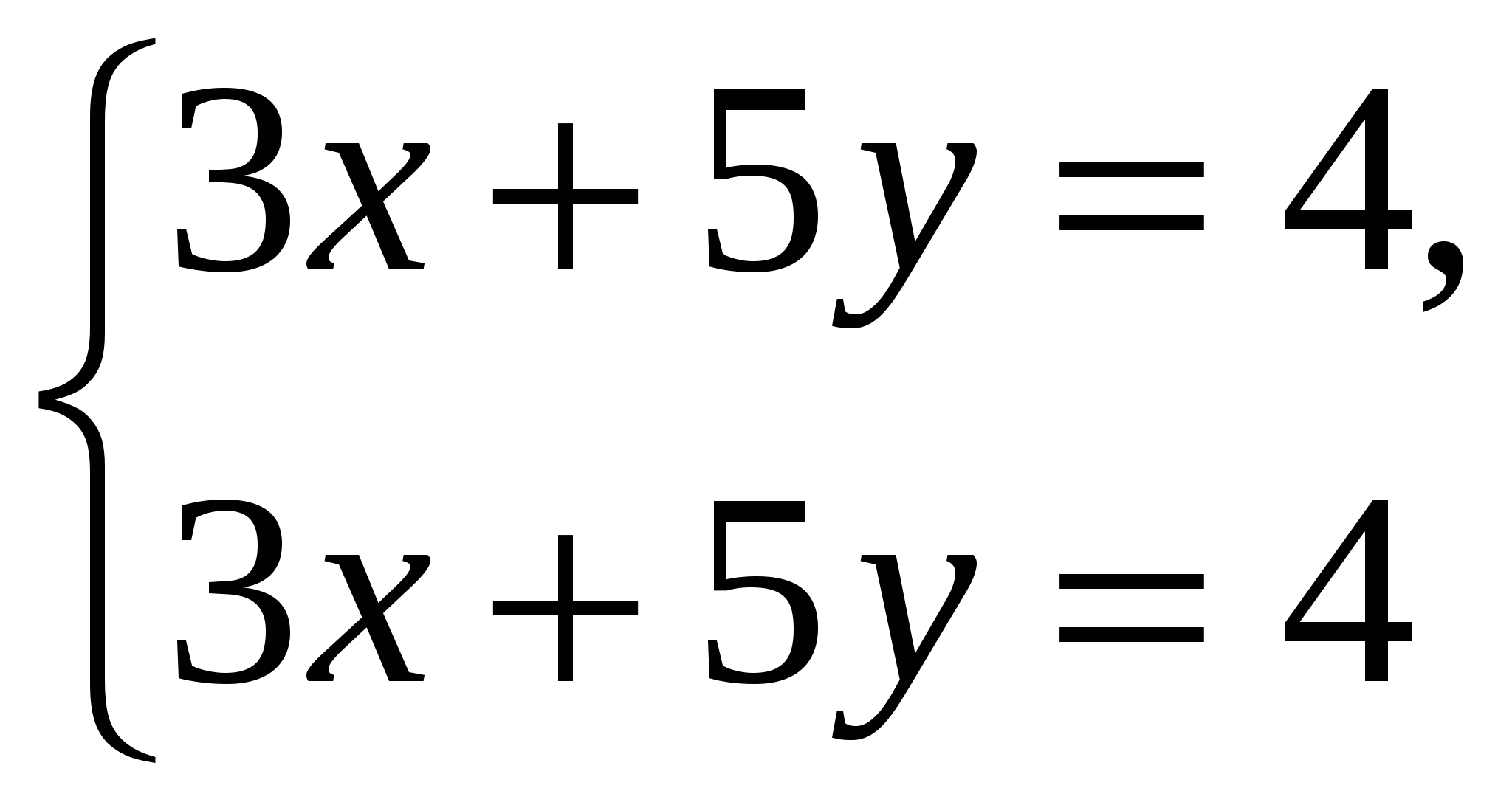 Оставим только одно из этих уравнений:  . Выразим через :  , значение - любое действительное число. Это и есть выражение для общего решения СЛУ. Ответ можно записать так:  , где  .Придавая различные значения, будем получать бесконечное множество частных решений. Например, при  получим  и первое частное решение  . При  получим  и второе частное решение  , и так далее. 2.2. Число уравнений и неизвестных равно 3 Рассмотрим СЛУ 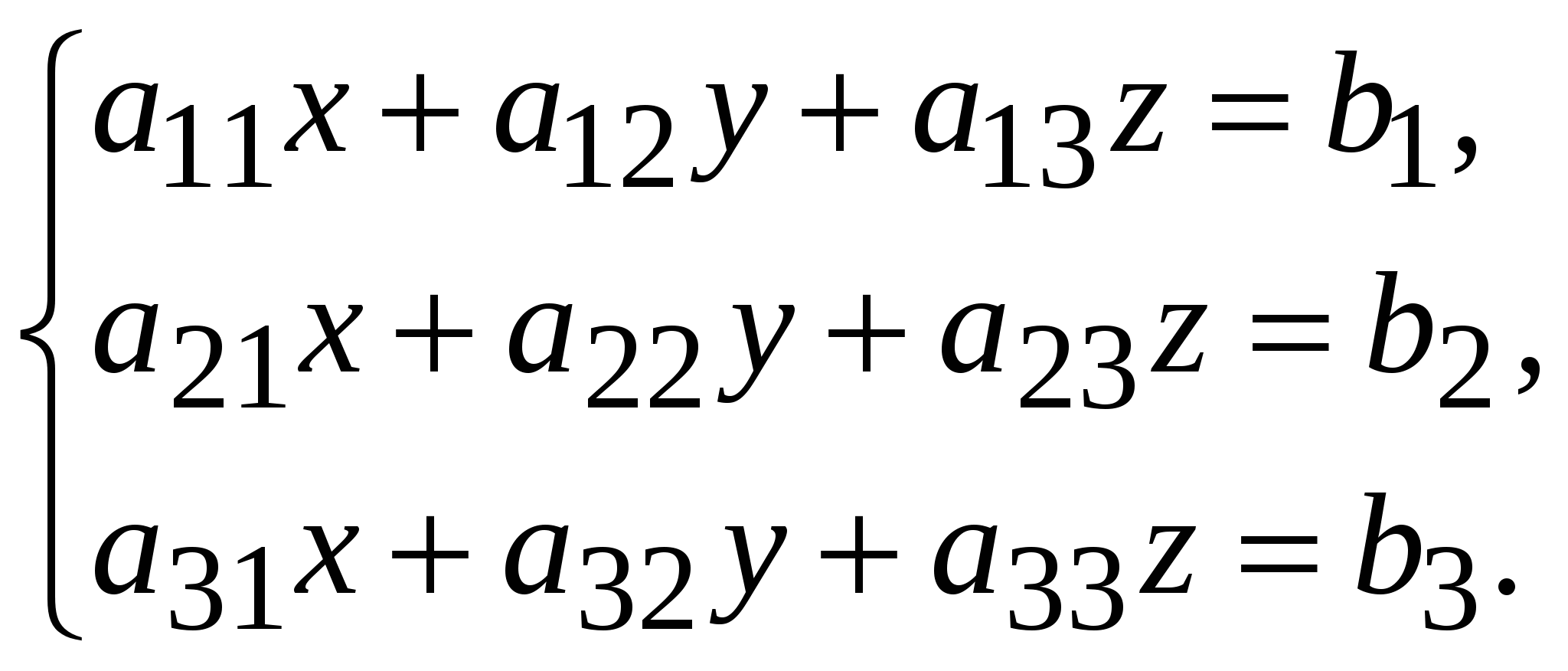 Вычисляются определители: 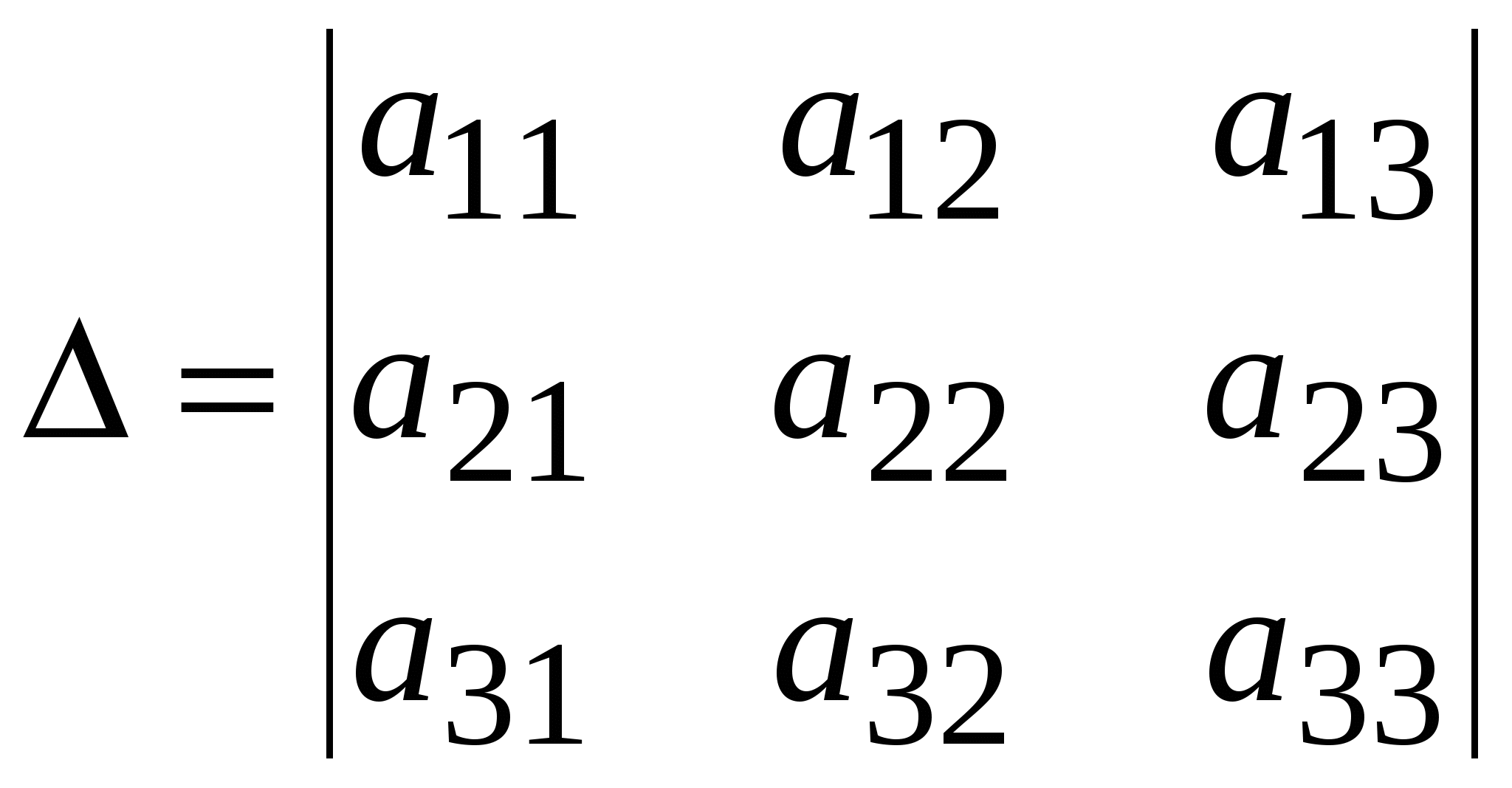 ,  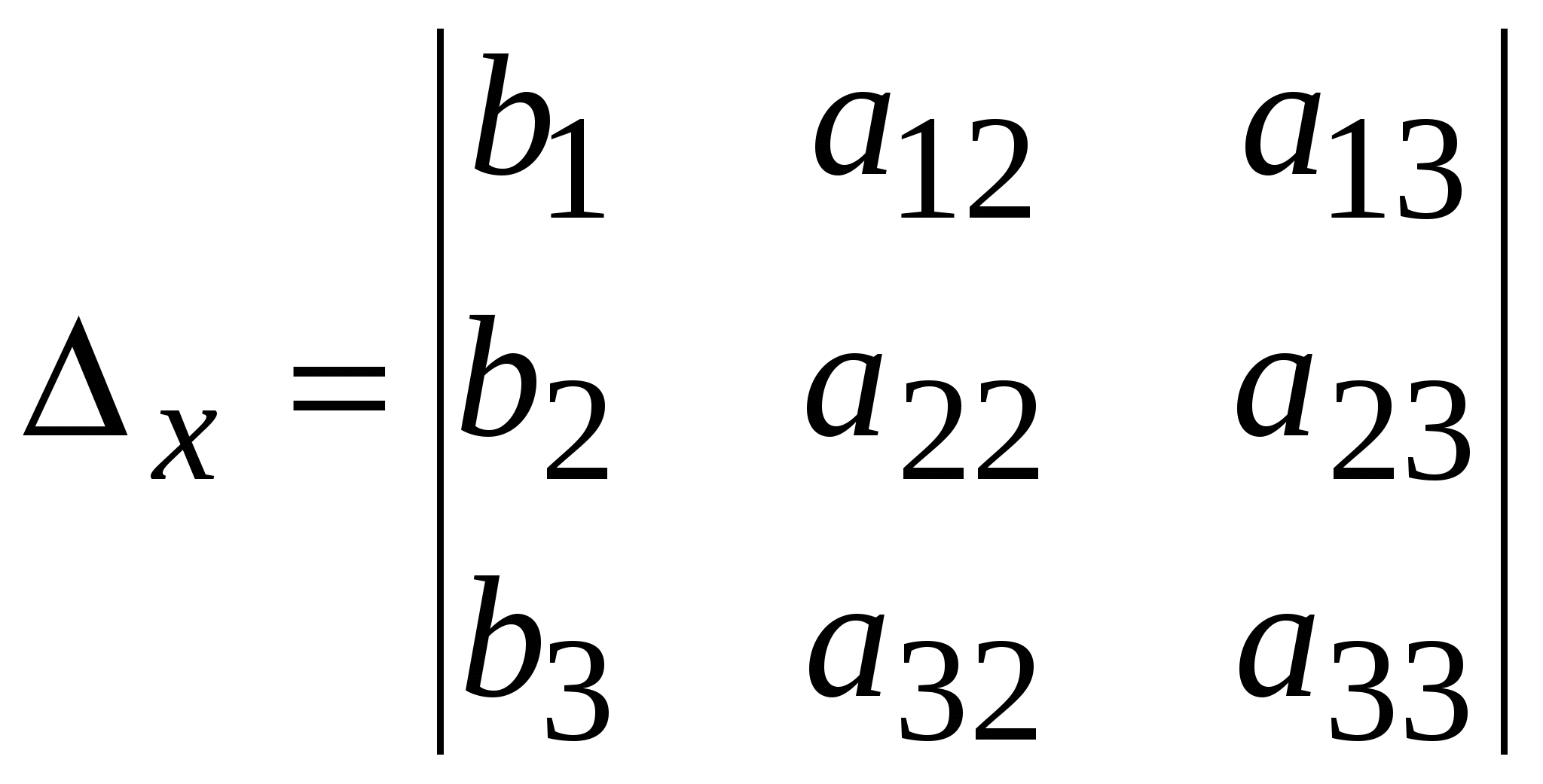,  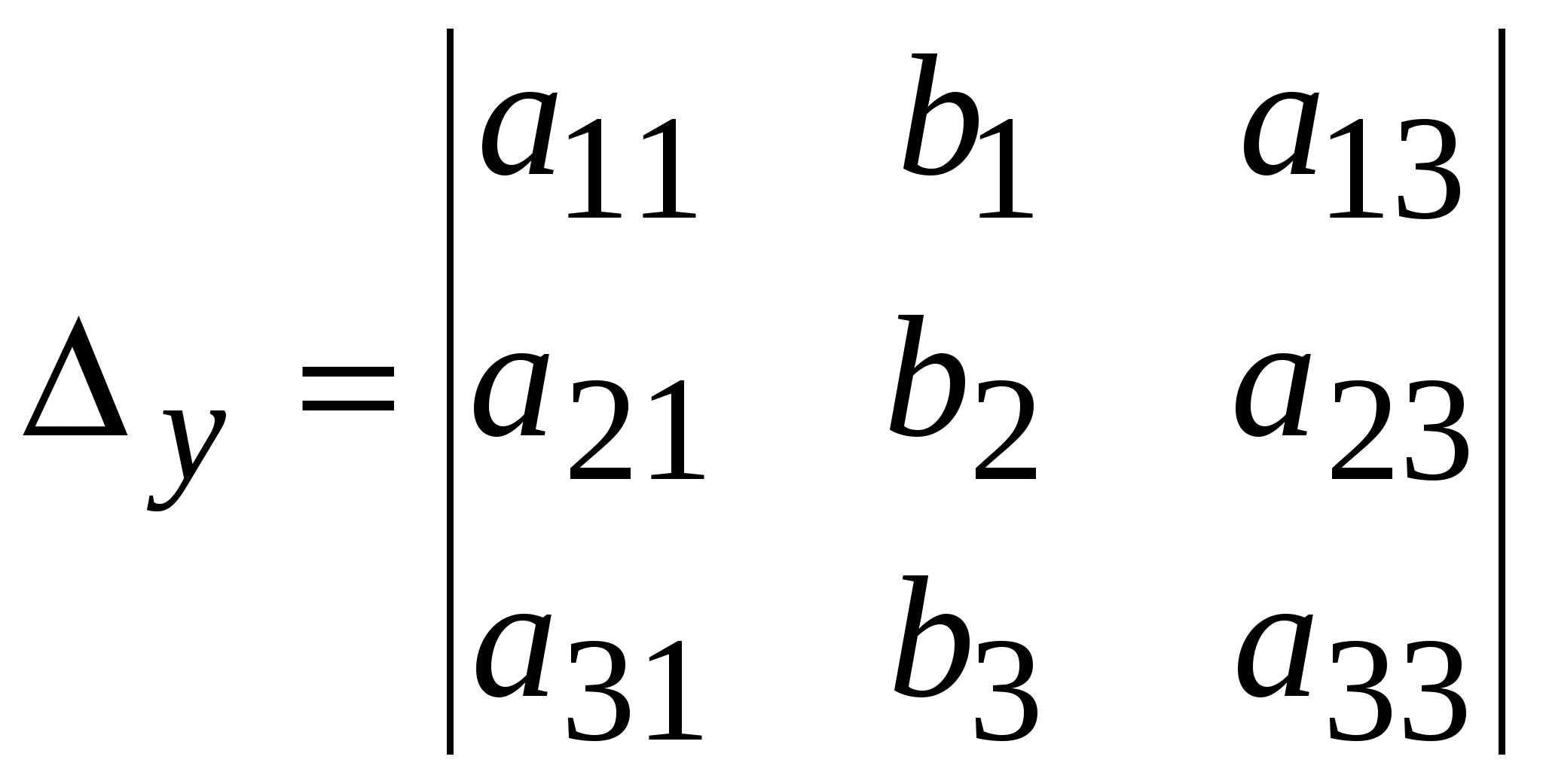,  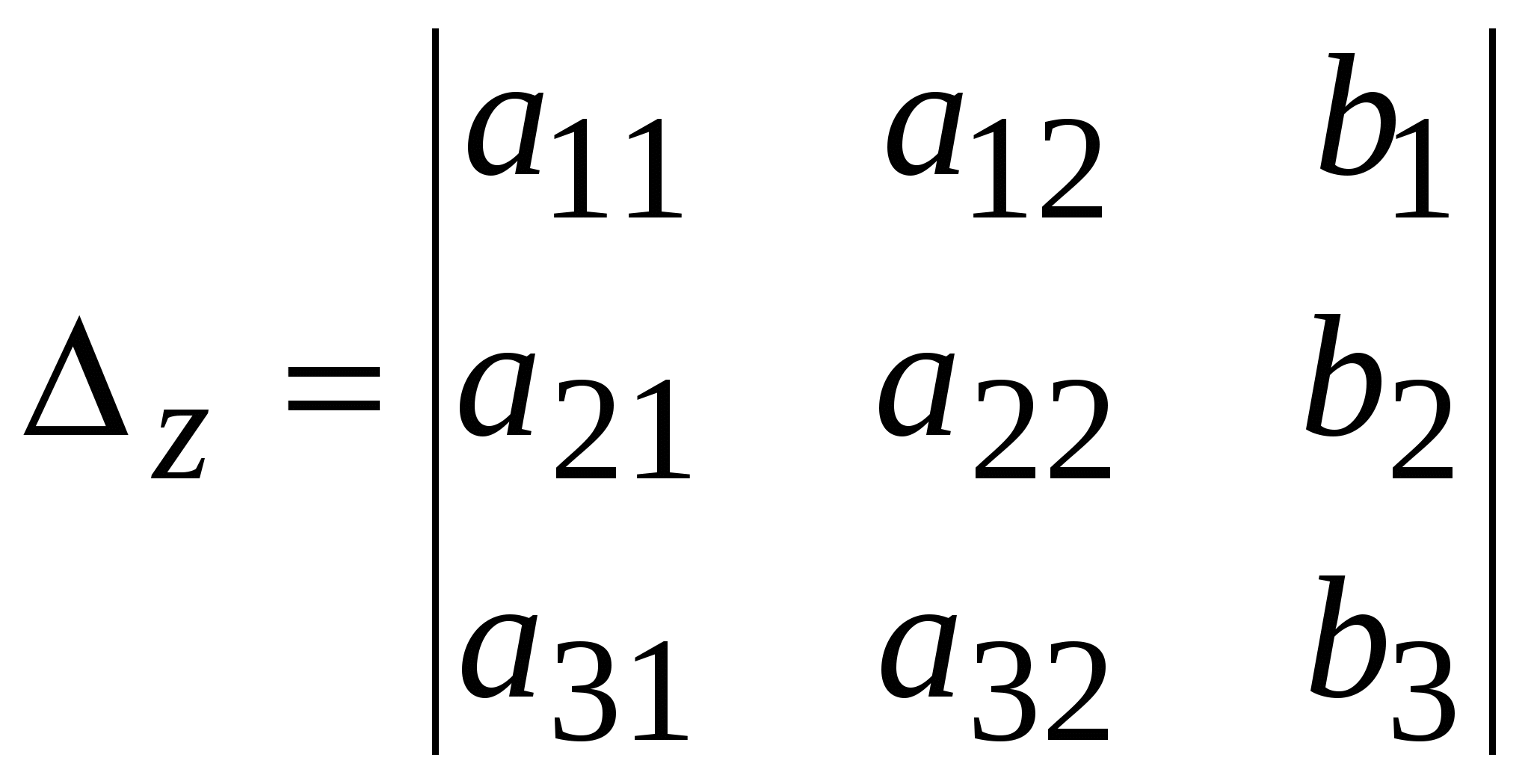.1. Если , то система имеет единственное решение, которое находится по формулам Крамера: ,  .2. Если , а хотя бы один из определителей , ,  отличен от нуля, то система не имеет решений. 3. Если  , то система имеет бесконечно много решений.Пример 4. Решить систему линейных уравнений 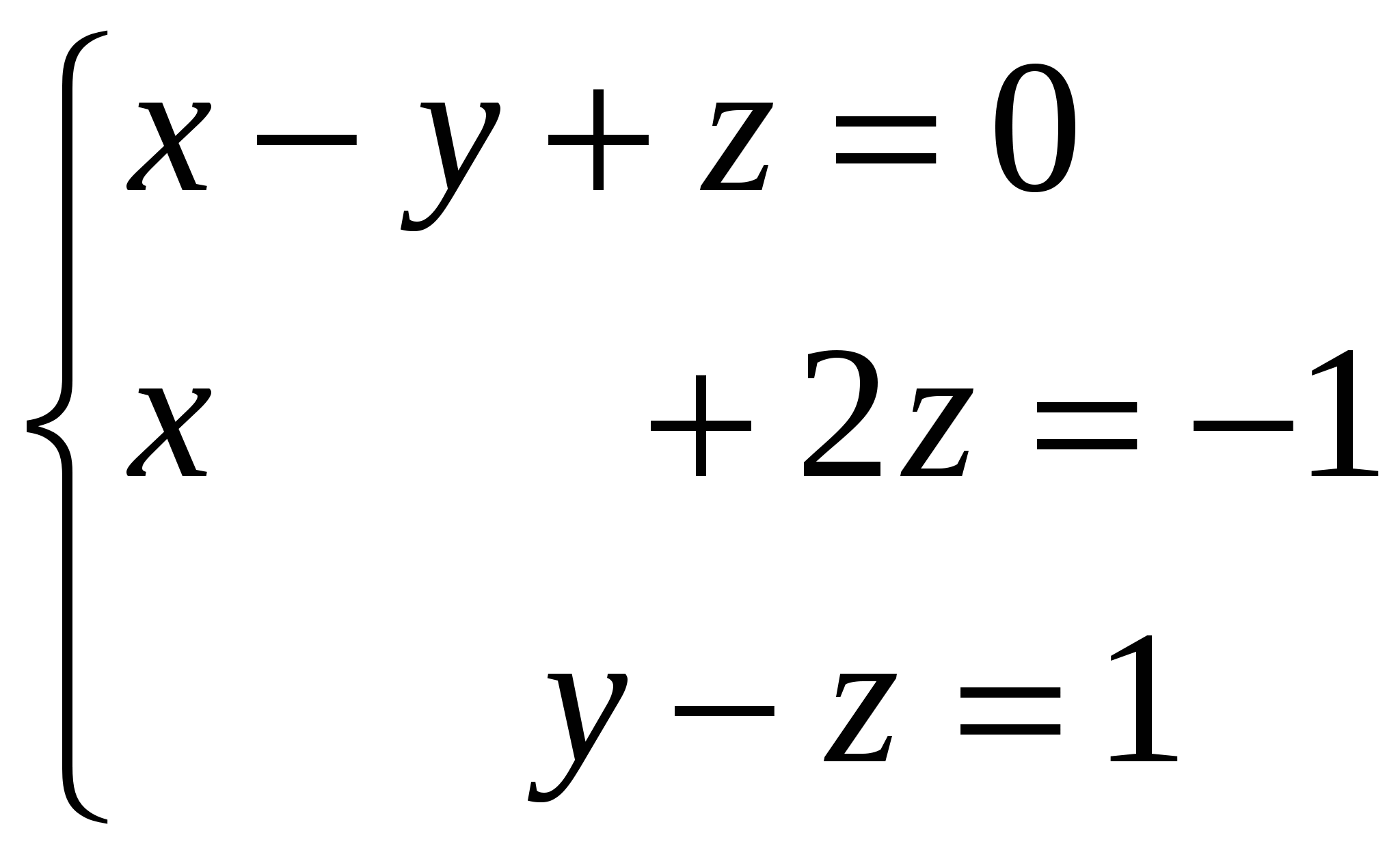 .Составим определитель из коэффициентов при неизвестных и вычислим его: 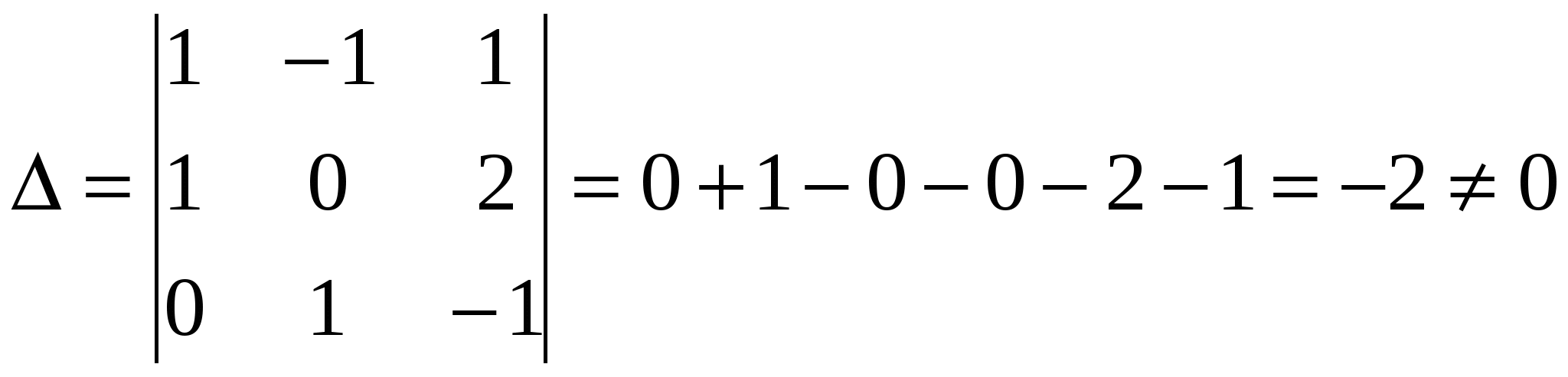 ,значит, СЛУ имеет единственное решение. Найдем вспомогательные определители и значения неизвестных. 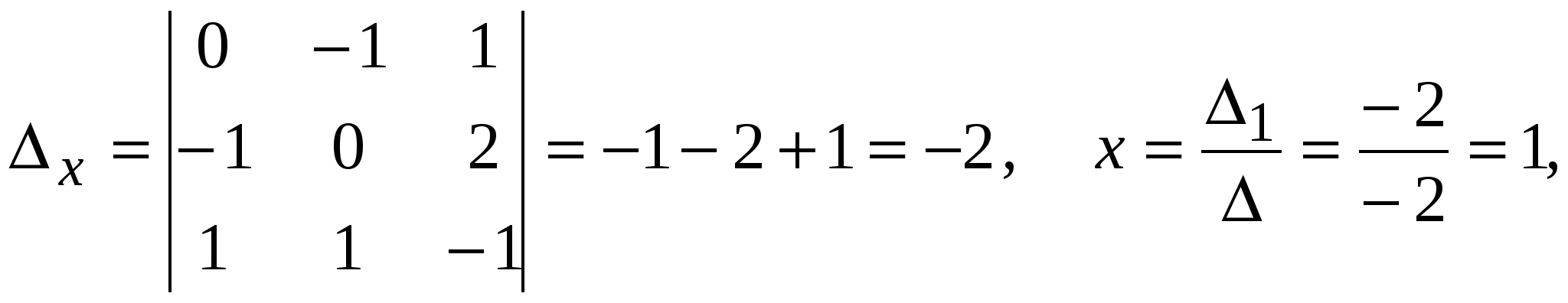 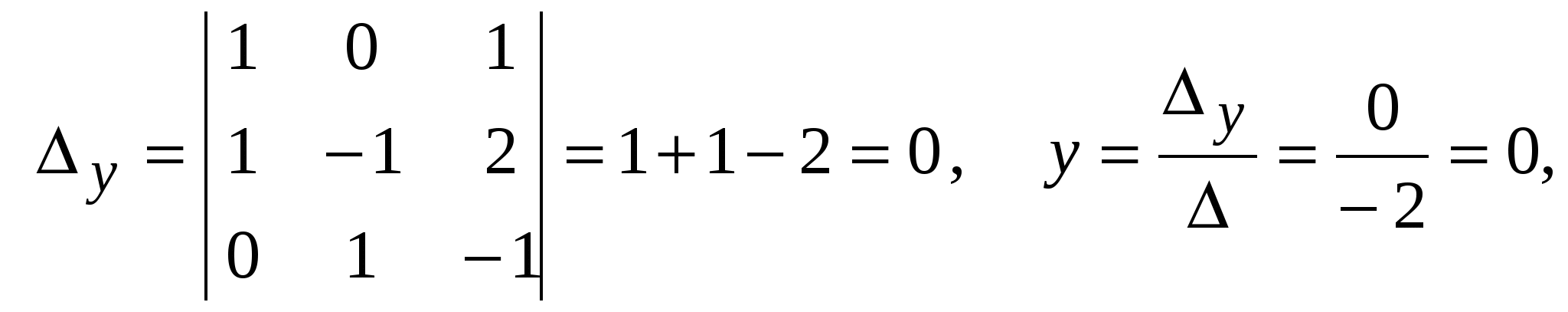 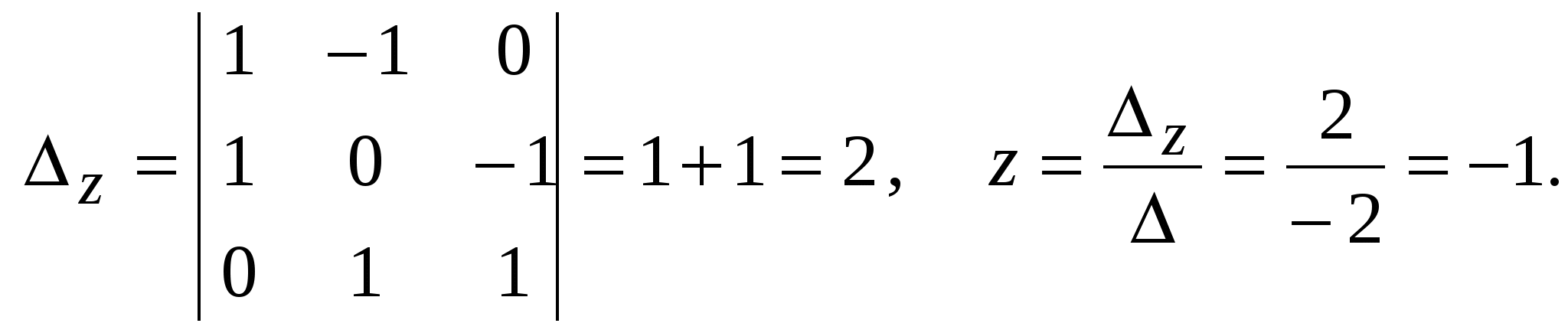  Ответ: Система совместная и определенная, единственное решение  .Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера. Пример 5. Решить СЛУ 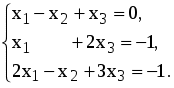 Решение Вычислим определитель системы: 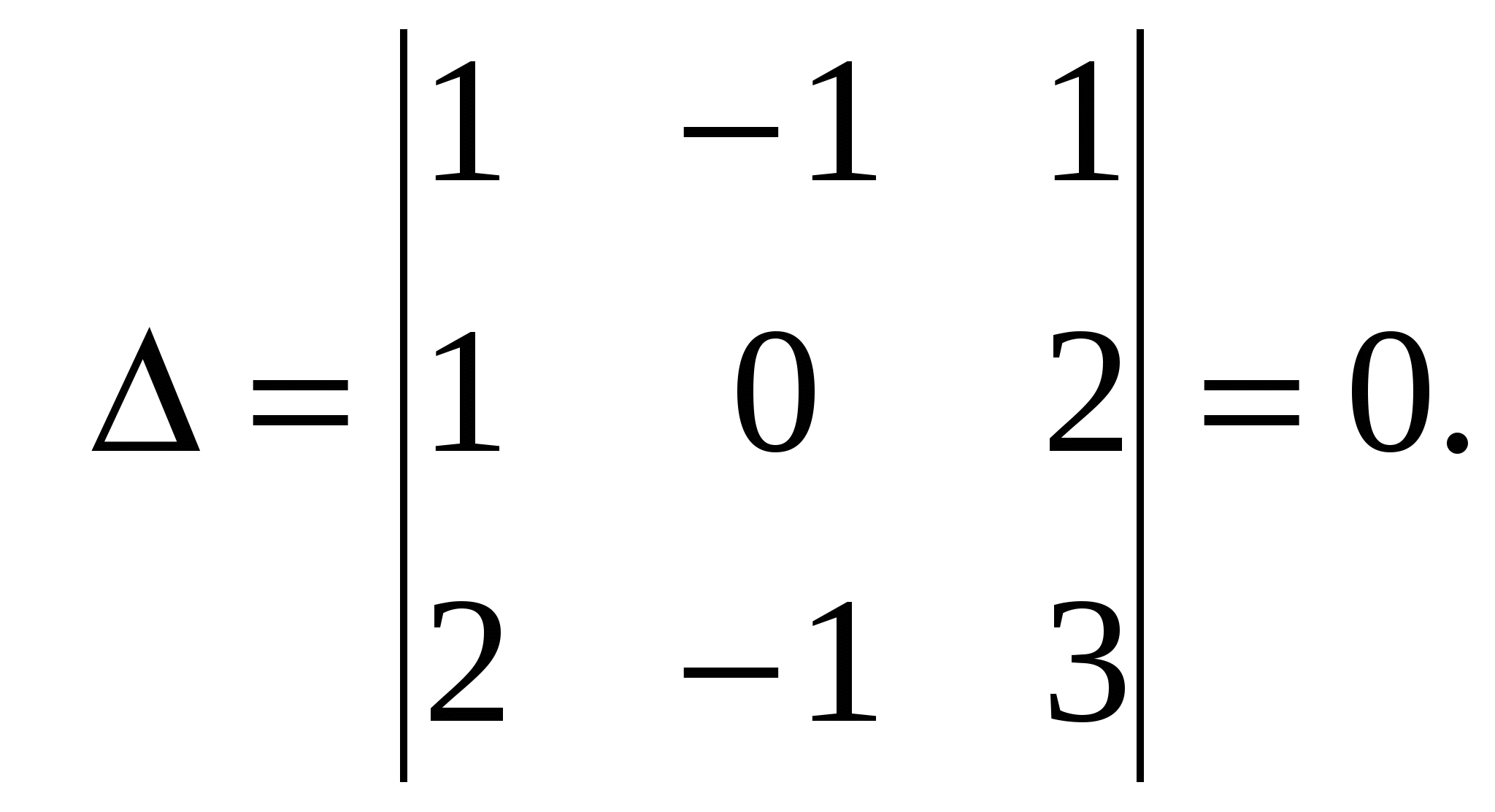 Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений. Отбросив третье уравнение, получим равносильную систему двух уравнений с тремя неизвестными: 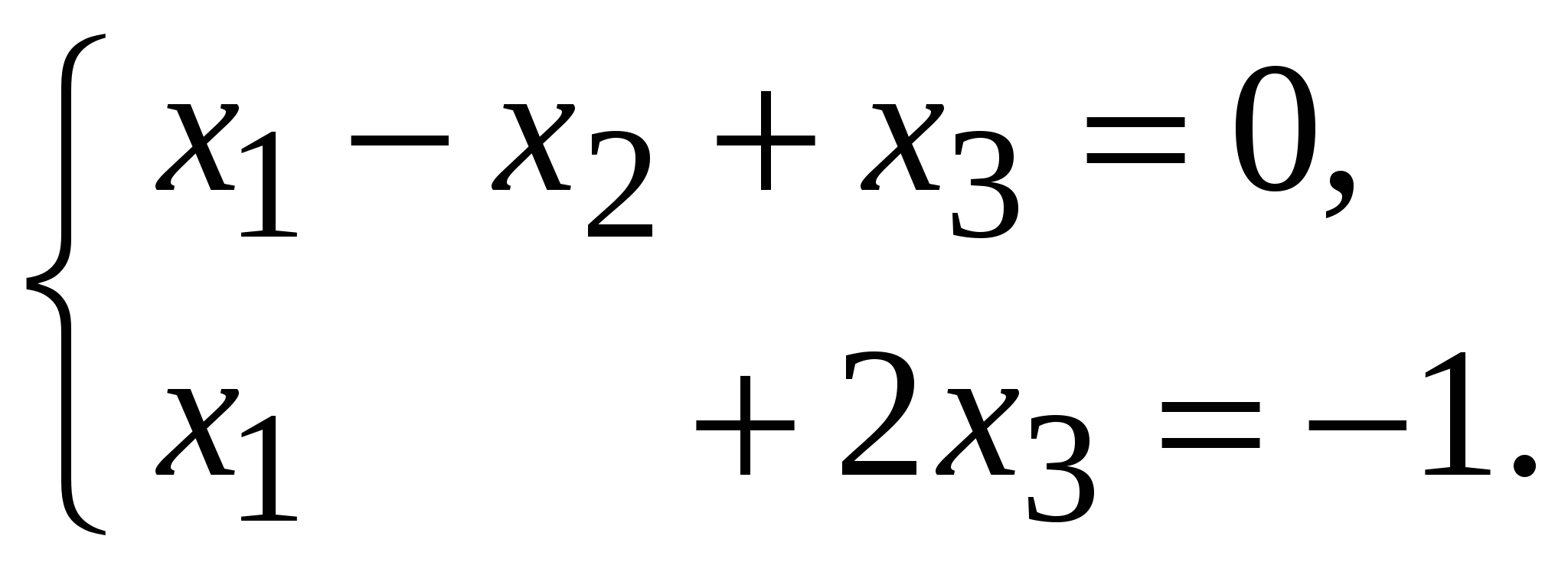 Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю. Например, коэффициенты при  и  образуют определитель  . Поэтому оставим в левой части уравнений слагаемые с и , а слагаемые с  перенесем в правую часть с противоположным знаком.Неизвестное  назовем свободным, а неизвестные  и  - базисными неизвестными. 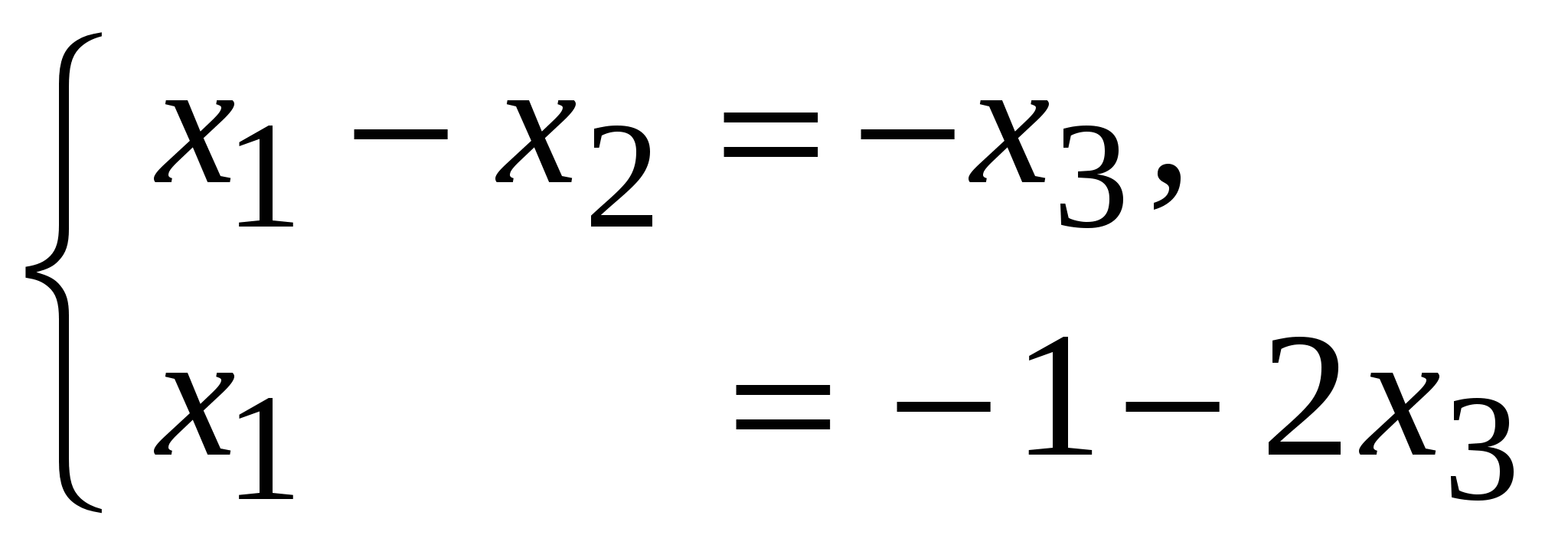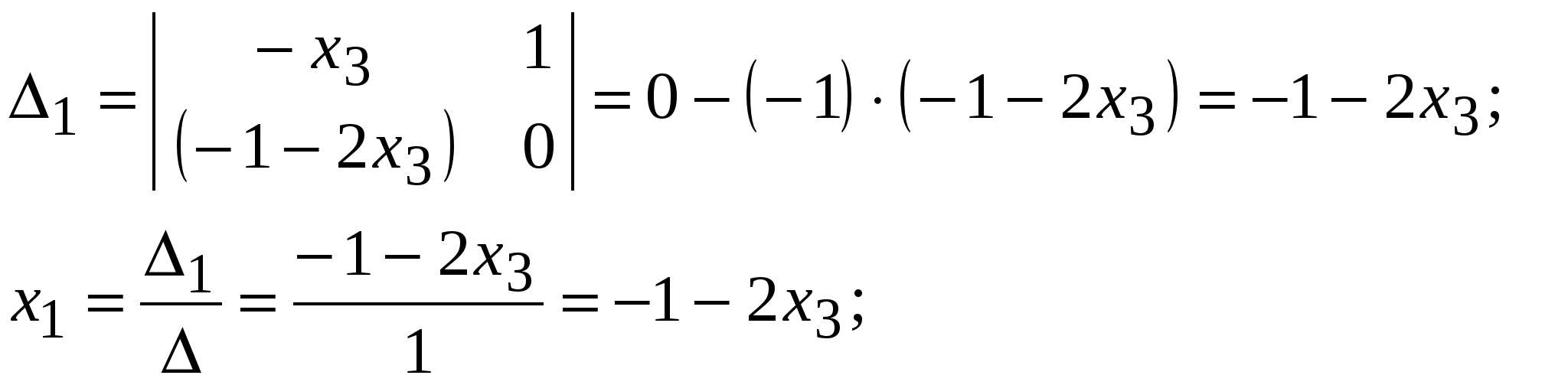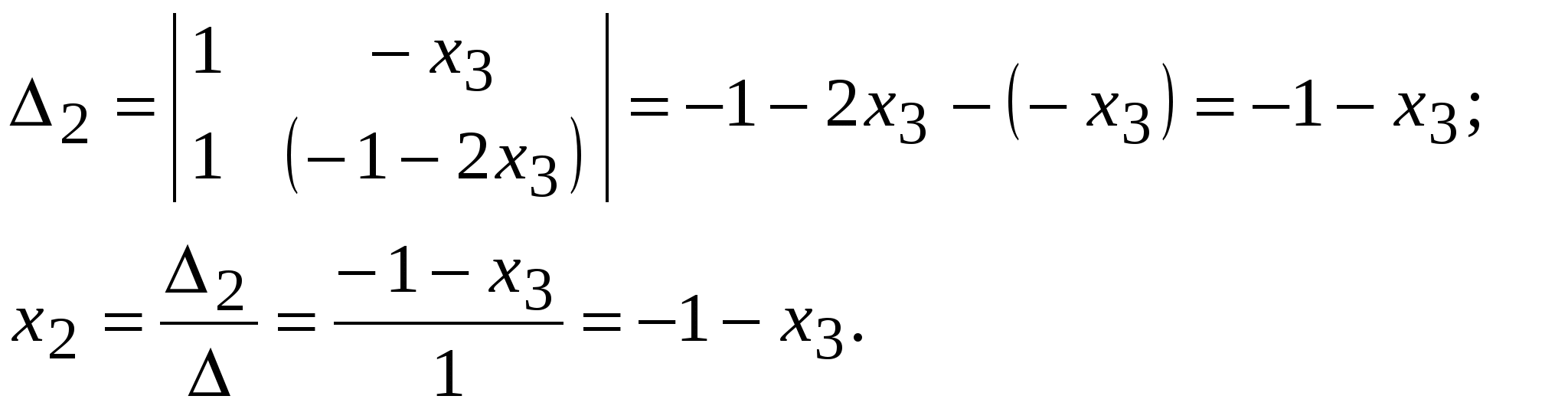Запишем систему в виде  и применим к ней правило Крамера: ; Выражение  -общее решение неопределенной СЛУ, где  - любое действительное число. Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение. Например, пусть  , тогда  ; тогда частное решение  . И так далее. Контрольные вопросы
|
линейных уравнений с 
неизвестными называется совокупность уравнений, в каждом из которых неизвестные 
присутствуют в первой степени: 
линейных уравнений с